多智能体强化学习算法【二】【MADDPG、QMIX、MAPPO】

相关文章：

 

常见多智能体强化学习仿真环境介绍【一】｛推荐收藏，真的牛｝

多智能体强化学习算法【一】【MAPPO、MADDPG、QMIX】

多智能体强化学习算法【二】【MADDPG、QMIX、MAPPO】

多智能体强化学习算法【三】【QMIX、MADDPG、MAPPO】

1. MADDPG

1.1 MADDPG简介

    本章介绍OpenAI 2017发表在NIPS 上的一篇文章，《Multi-Agent Actor-Critic for Mixed Cooperative-Competitive Environments》。主要是将AC算法进行了一系列改进，使其能够适用于传统RL算法无法处理的复杂多智能体场景。

    传统RL算法面临的一个主要问题是由于每个智能体都是在不断学习改进其策略，因此从每一个智能体的角度看，环境是一个动态不稳定的，这不符合传统RL收敛条件。并且在一定程度上，无法通过仅仅改变智能体自身的策略来适应动态不稳定的环境。由于环境的不稳定，将无法直接使用之前的经验回放等DQN的关键技巧。policy gradient算法会由于智能体数量的变多使得本就有的方差大的问题加剧。

    MADDPG算法具有以下三点特征： 1. 通过学习得到的最优策略，在应用时只利用局部信息就能给出最优动作。 2. 不需要知道环境的动力学模型以及特殊的通信需求。 3. 该算法不仅能用于合作环境，也能用于竞争环境。

MADDPG算法具有以下三点技巧：

1. 集中式训练，分布式执行：训练时采用集中式学习训练critic与actor，使用时actor只用知道局部信息就能运行。critic需要其他智能体的策略信息，本文给了一种估计其他智能体策略的方法，能够只用知道其他智能体的观测与动作。
2. 改进了经验回放记录的数据。为了能够适用于动态环境，每一条信息由 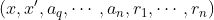组成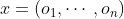表示每个智能体的观测。
3. 利用策略集合效果优化（policy ensemble）：对每个智能体学习多个策略，改进时利用所有策略的整体效果进行优化。以提高算法的稳定性以及鲁棒性。

其实MADDPG本质上还是一个DPG算法，针对每个智能体训练一个需要全局信息的Critic以及一个需要局部信息的Actor，并且允许每个智能体有自己的奖励函数（reward function），因此可以用于合作任务或对抗任务。并且由于脱胎于DPG算法，因此动作空间可以是连续的。

1） DQN

DQN的思想就是设计一个不断逼近真实的函数。其中主要用到了两个技巧：1. 经验回放。2. 目标网络。该技巧主要用来打破数据之间联系，因为神经网络对数据的假设是独立同分布，而MDP过程的数据前后有关联。打破数据的联系可以更好地拟合函数。其代价函数为：

其中表示目标网络，其参数更新与不同步（滞后）。具体可以参看值函数强化学习-DQN、DDQN和Dueling DQN算法公式推导分析。

2）SPG（stochastic policy gradient）

SPG算法不采用拟合Q函数的方式，而是直接优化累积回报来获得使回报最大的策略。假定参数化的策略为，累积回报为。为了使最大化，直接对策略参数求导得到策略更新梯度：

AC算法也可以由此推出，如果按照DQN的方法拟合一个函数，则这个参数化的函数被称为Critic，被称为Actor。具体可以参看，随机策略梯度算法（stochastic-policy-gradient）。

3) DPG

上述两种算法都是针对随机策略，  是一个在状态s对于各个动作a的条件概率分布。DPG针对确定性策略，  是一个状态空间到动作空间的映射。其思想与SPG相同，得到策略梯度公式为

DPG可以是使用AC的方法来估计一个Q函数，DDPG就是借用了DQN经验回放与目标网络的技巧，具体可以参看，确定性策略强化学习-DPG&DDPG算法推导及分析。

1.2 MADDPG原理设计技巧

1.2.1 多智能体AC设计

MADDPG集中式的学习，分布式的应用。因此我们允许使用一些额外的信息（全局信息）进行学习，只要在应用的时候使用局部信息进行决策就行。这点就是Q-learning的一个不足之处，Q-learning在学习与应用时必须采用相同的信息。所以这里MADDPG对传统的AC算法进行了一个改进，Critic扩展为可以利用其他智能体的策略进行学习，这点的进一步改进就是每个智能体对其他智能体的策略进行一个函数逼近。

我们用表示n个智能体策略的参数，  表示n个智能体的策略。针对第i个智能体的累积期望奖励  ，针对随机策略，求策略梯度为：

其中表示第i个智能体的观测，  表示观测向量，即状态。  表示第i个智能体集中式的状态-动作函数。由于是每个智能体独立学习自己的函数，因此每个智能体可以有不同的奖励函数（reward function），因此可以完成合作或竞争任务。

上述为随机策略梯度算法，下面我们拓展到确定性策略  ，梯度公式为

由以上两个梯度公式可以看出该算法与SPG与DPG十分类似，就像是将单体直接扩展到多体。但其实是一个非常厉害的技巧，针对每个智能体建立值函数，极大的解决了传统RL算法在Multi-agent领域的不足。D是一个经验存储（experience replay buffer），元素组成为  。集中式的critic的更新方法借鉴了DQN中TD与目标网络思想

  表示目标网络，  为目标策略具有滞后更新的参数  。其他智能体的策略可以采用拟合逼近的方式得到，而不需要通信交互。

如上可以看出critic借用了全局信息学习，actor只是用了局部观测信息。MADDPG的一个启发就是，如果我们知道所有的智能体的动作，那么环境就是稳定的，就算策略在不断更新环境也是恒定的，因为模型动力学使稳定的 :

1.2.2 估计其他智能体策略

在(1)式中，我们用到了其他智能体的策略，这需要不断的通信来获取，但是也可以放宽这个条件，通过对其他智能体的策略进行估计来实现。每个智能体维护n-1个策略逼近函数表示第i个智能体对第j个智能体策略的函数逼近。其逼近代价为对数代价函数，并且加上策略的熵，其代价函数可以写为:

只要最小化上述代价函数，就能得到其他智能体策略的逼近。因此可以替换(1)式中的y。

在更新之前，利用经验回放的一个采样batch更新  。

1.2.3. 策略集合优化（policies ensemble）

这个技巧也是本文的一个亮点。多智能体强化学习一个顽固的问题是由于每个智能体的策略都在更新迭代导致环境针对一个特定的智能体是动态不稳定的。这种情况在竞争任务下尤其严重，经常会出现一个智能体针对其竞争对手过拟合出一个强策略。但是这个强策略是非常脆弱的，也是我们希望得到的，因为随着竞争对手策略的更新改变，这个强策略很难去适应新的对手策略。

为了能更好的应对上述情况，MADDPG提出了一种策略集合的思想，第i个智能体的策略  由一个具有K个子策略的集合构成，在每一个训练episode中只是用一个子策略  （简写为  ）。对每一个智能体，我们最大化其策略集合的整体奖励  。

并且我们为每一个子策略k构建一个记忆存储  。我们优化策略集合的整体效果，因此针对每一个子策略的更新梯度为:

以上就是MADDPG所有的内容，仿真效果也很好的证明了MADDPG在多智能体系统中的有效性。 MADDPG是OpenAI给的仿真代码。