LSTM系列的梯度问题

1.前沿

本文主要围绕NN、RNN、LSTM和GRU，讨论后向传播中所存在的梯度问题，以及解决方法，力求深入浅出。

2.神经网络开始

神经网络包括前向过程和后向过程，前向过程定义网络结构，后向过程对网络进行训练（也就是优化参数），经过多轮迭代得到最终网络（参数已定）
我们先来分析一个非常简单的三层神经网络：

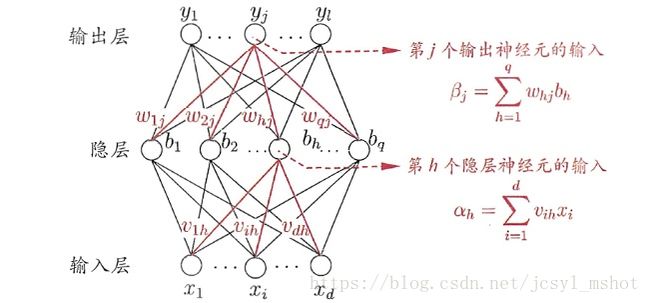
数据集 D=(x1,y1),(x2,y2),...,(xm,ym) D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m )

2.1前向过程：

在输入层，假设该层节点数为d，也就是特征x的维度， xi x i 作为该层输出；

在隐藏层中，该层节点数为q，每个节点的输入 αh α h 就是上一层所有节点输出 xi x i 的线性组合值，该节点的输出 bh是αj b h 是 α j 的激活值，这里假设使用sigmoid激活函数；

在输出层，该层节点数为l，也就是输出y的维度，同理，每个节点的输入 βj β j 是 bh b h 的线性组合值，输出 y′j是βj的激活值 y j ′ 是 β j 的 激 活 值 ，根据不同任务选择不同激活函数，比如二分类任务一般是用sigmoid激活函数把 y′j限制到[0,1]之间。 y j ′ 限 制 到 [ 0 , 1 ] 之 间 。

2.2后向过程

1）首先我们根据网络输出和真实Label来定义Loss函数，这里定义为简单的均方误差：

Ek=12∑lj=1(y′j−yj)2 E k = 1 2 ∑ j = 1 l ( y j ′ − y j ) 2

那么我们的目标就是最小化Loss，调整参数 w_{hj} 和 v_{ih} ，使得网络尽量去拟合真实数据。如何求最小值？那当然是求导了，根据loss函数对参数求导，然后往梯度下降的方向去更新参数，可以降低loss值。梯度主宰更新，如果梯度太小，会带来梯度消失问题，导致参数更新很慢；那如果梯度很大，又会造成梯度爆炸问题。

2）对于输出层参数 wij，E对whj w i j ， E 对 w h j 进行链式求导，也就是，E先对节点的输出 y′j y j ′ 求导，再对节点的输入 βj β j 求导，最后 对 whj w h j 求导，结果为：
∂E∂whj=∂E∂y′j∂y′j∂βj∂βj∂whj=(y′j−yj)⋅y′j(1−y′j⋅bh ∂ E ∂ w h j = ∂ E ∂ y j ′ ∂ y j ′ ∂ β j ∂ β j ∂ w h j = ( y j ′ − y j ) ⋅ y j ′ ( 1 − y j ′ ⋅ b h

这里我们令 gj=(y′j−yj)⋅y′j(1−y′j) g j = ( y j ′ − y j ) ⋅ y j ′ ( 1 − y j ′ ) ，就可以得到参数 whj w h j 的更新量为：

Δwhj=−η⋅gj⋅bh Δ w h j = − η ⋅ g j ⋅ b h

3）对于隐藏层参数 vih v i h ，也是链式求导，E先对该层节点的输出 bj b j 求导，再对节点的输入 αj α j 求导，最后对 vih v i h 求导，其实在前面我们已经求出了部分梯度，最后结果为：
∂E∂vih=∂E∂bh∂bh∂αh∂αh∂vih=(∑lj=1∂E∂y′j∂y′j∂βj∂βj∂bh)⋅∂bh∂αh⋅∂αh∂vih ∂ E ∂ v i h = ∂ E ∂ b h ∂ b h ∂ α h ∂ α h ∂ v i h = ( ∑ j = 1 l ∂ E ∂ y j ′ ∂ y j ′ ∂ β j ∂ β j ∂ b h ) ⋅ ∂ b h ∂ α h ⋅ ∂ α h ∂ v i h

注意到， ∂E∂y′j∂y′j∂βj ∂ E ∂ y j ′ ∂ y j ′ ∂ β j 其实我们刚刚求过，其实就是 gj g j 这货，因此我们可得：
∂E∂vih=(∑lj=1gj⋅whj)⋅bh(1−bh)⋅xi ∂ E ∂ v i h = ( ∑ j = 1 l g j ⋅ w h j ) ⋅ b h ( 1 − b h ) ⋅ x i

再次令 eh=(∑lj=1gj⋅whj)⋅bh(1−bh)  e h = ( ∑ j = 1 l g j ⋅ w h j ) ⋅ b h ( 1 − b h )   ，可以得到 vih v i h 的更新量为：

Δvih=−η⋅eh⋅xi Δ v i h = − η ⋅ e h ⋅ x i

也就可以愉快地将更新 vih=vih+Δvih v i h = v i h + Δ v i h 了。

2.3 等等，事情好像并没有这么简单

1） gj g j ：这是上一层传递过来的梯度，如果上一层的梯度本来已经很小，那么在这一层进行相乘，会导致这一层的梯度也很小。所以如果网络层比较深，那么在链式求导的过程中，越是低层的网络层梯度在连乘过程中可能会变得越来越小，导致梯度消失。

2） whj w h j ：这是这一层的权重，这一项是造成梯度爆炸的主要原因，如果权重很大，也可能会导致相乘后的梯度也比较大。（梯度爆炸不是问题，做个梯度裁剪就行了，对梯度乘以一个缩放因子，我们主要考虑的是梯度消失问题）

3） bh(1−bh) b h ( 1 − b h ) ：这是sigmoid激活函数的导数，sigmoid激活值本身已经是一个比较小的数了，这两个小于1的数相乘会变得更小，就可能会造成梯度消失。

我们直接来看sigmoid的这个图吧，只有在靠近0的区域梯度比较大（然而也不会超过0.25），在接近无穷小或者无穷大的时候梯度几乎是0了：

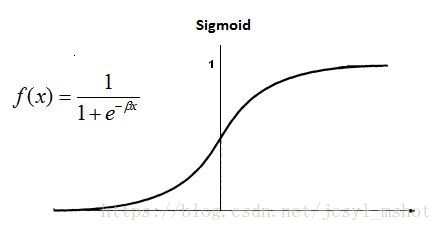
所以sigmoid是造成梯度消失的一个重要原因，激活函数其实是为了引入了非线性操作，使得神经网络可以逼近非线性函数。因此如果不是输出层必须要用sigmoid来限制输出范围，我一般是不用sigmoid的。

那么从激活函数出发，缓解梯度消失有以下方法：
1）不行就换，比如把sigmoid换成relu，在x>0的时候可以稳稳维持1的梯度。

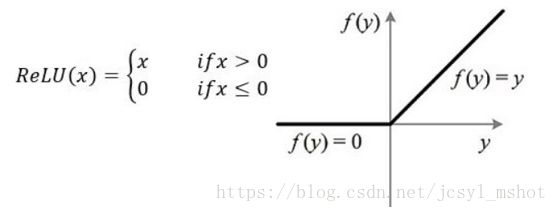
2）不想换那也行，既然我们知道sigmoid在靠近0的取值范围内梯度比较大，但我们可以把数据尽量规范化到一个比较合适的范围，也就是接下来要谈到的Normaliztion。

3. 从RNN到LSTM再到GRU

接下来我们再探讨一下RNN系列，也就是展开型的神经网络。

3.1 RNN

RNN是最简单的循环神经网络，其实就是对神经网络展开k个step，所有step共享同一个神经网络模块S，我们还是直接来看图吧：

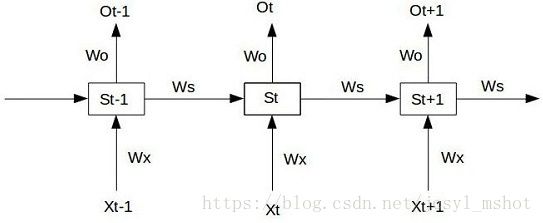
这是一个序列预测任务，可以看到在RNN中 W_s 和 W_x这两个参数是共享的，注意噢：这里也有个共享的W_o ，但不是包含在RNN中的，只是用于序列预测而已。

在step t下，RNN的输出向量 st s t 是：

st=tanh(Wxxt+Wsst−1+b) s t = t a n h ( W x x t + W s s t − 1 + b )

接下来 Wo和st W o 和 s t 进行相乘得到step t下的预测值 ot o t （加激活函数也可以）。假设step t 的正确label是 yt y t ，我们现在还是将Loss函数定义为均方误差：
E=12∑Tt=1(yt−ot)2 E = 1 2 ∑ t = 1 T ( y t − o t ) 2 .

现在我们来看看怎么更新W_x，可以看到在step t 下，计算 o_t 不仅涉及到了step t下的W_x ，也涉及到了前面step下的W_x，来看这个反向传播路径图：

因此在step t下， Et对wx E t 对 w x 求导需要对前面所有step的 Wx W x 依次进行求导，再加起来：

∂Et∂Wx=∑ti=1∂Et∂ot∂ot∂st(∏tj=i+1∂sj∂sj−1)∂si∂Wx ∂ E t ∂ W x = ∑ i = 1 t ∂ E t ∂ o t ∂ o t ∂ s t ( ∏ j = i + 1 t ∂ s j ∂ s j − 1 ) ∂ s i ∂ W x

注意到有一个硕大的连乘符号，事情好像又开始变得不简单起来，我们来继续求导下去，在RNN中 s的激活函数是tanh函数：

∏tj=i+1∂sj∂sj−1=∏tj=i+1tanh′⋅Ws ∏ j = i + 1 t ∂ s j ∂ s j − 1 = ∏ j = i + 1 t t a n h ′ ⋅ W s

路和前面的神经网络是一样的！这里又涉及到了激活函数的梯度，以及网络的其它权重 Ws W s ，而tanh其实只是将sigmoid的范围从[0, 1]变到[-1, 1]而已：

另外，我们从矩阵的角度来看， ∂sj∂sj−1 ∂ s j ∂ s j − 1 是个Jacobian矩阵（向量对向量求导），如果矩阵值太大显然会带来梯度爆炸（这个不是重点），重点是如果值比较小，而且又经过矩阵连乘，梯度值迅速收缩，最后可能会造成梯度消失。

刚刚我们推导了 W_x的梯度， W_s其实也是一样的，这里不再重复推导。而 W_o，前面讲到它不是属于RNN的，但是我们也不妨来推导一下：

∂EtWo=∂Et∂ot⋅∂ot∂Wo ∂ E t W o = ∂ E t ∂ o t ⋅ ∂ o t ∂ W o

咦！没错，在step t下， ot o t 只和这个step的 Wo W o 有关，和前面step的 Wo W o 都没关系，所以 Wo W o 的梯度对我们并没有什么威胁。

3.2 LSTM出场

上面讲到，RNN的梯度问题是产生于 ∏tj=i+1∂sj∂sj−1 ∏ j = i + 1 t ∂ s j ∂ s j − 1 这一项，LSTM作为RNN的改进版本，改进了共享的神经网络模块，引入了cell结构，其实也是为了在这一项中保持一定的梯度，把连乘操作改为连加操作。

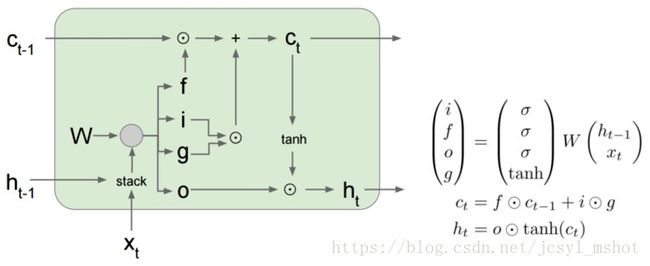
LSTM相信很多人看过这个：[译] 理解 LSTM 网络，但是我发现cs231n的公式更加简洁，把四个门层结构的权重参数合成一个W

求导过程比较复杂，我们先看一下c_t这一项：

ct=ft⋅ct−1+it⋅gt c t = f t ⋅ c t − 1 + i t ⋅ g t

和前面一样，我们来求一下 ∂ct∂ct−1 ∂ c t ∂ c t − 1 ，这里注意 ft，it和gt f t ， i t 和 g t 都是 ct−1 c t − 1 的复合函数：

∂ct∂ct−1=ft+∂ft∂ct−1⋅ct−1+... ∂ c t ∂ c t − 1 = f t + ∂ f t ∂ c t − 1 ⋅ c t − 1 + . . .

后面的我们就不管了，展开求导太麻烦了，第一项 ft f t 是什么！大声告诉我！ ft f t 是forget gate的输出值，1表示完全保留旧状态，0表示完全舍弃旧状态，那如果我们把 f_t设置成1或者是接近于1，那 ∂ct∂ct−1 ∂ c t ∂ c t − 1 这一项就有妥妥的梯度了。

因此LSTM是靠着cell结构来保留梯度，forget gate控制了对过去信息的保留程度，如果gate选择保留旧状态，那么梯度就会接近于1，可以缓解梯度消失问题。这里说缓解，是因为LSTM只是在 c_t到 c_{t-1}这条路上解决梯度消失问题，而其他路依然存在梯度消失问题。

而且forget gate解决了RNN中的长期依赖问题，不管网络多深，也可以记住之前的信息。

另外，LSTM可以缓解梯度消失，但是梯度爆炸并不能解决，但实际上前面也讲过，梯度爆炸不是什么大问题。

3.3GRU

略

4.从Batch Normalization到Group Normalization

现在我们已经知道：

1）激活函数对梯度也有很大的影响，大部分激活函数只在某个区域内梯度比较好。

2）在后向传播的时候，我们需要进行链式求导，如果网络层很深，激活函数有权重又小，会导致梯度消失；如果权重很大，又会导致梯度爆炸。

那么解决梯度消失可以从这几方面入手：

1）换激活函数；2）调整激活函数的输入；3）调整网络结构

事实上，我们有一个好东西可以解决梯度问题，叫做Normalization，就是从第二方面入手同时解决梯度消失和爆炸，而且也可以加快训练速度。

4.1Batch Normalization

假设对于一个batch内某个维度的特征 {{x_1, x_2, …, x_m}}，

BN需要将其转化成 {{y_1, y_2, …, y_m}}，

首先对节点的线性组合值进行归一化，使其均值是0，方差是1。（也就是，对节点的输入进行归一化，而不是对输出进行归一化）

x′i=xi−μσ2+ε√ x i ′ = x i − μ σ 2 + ε

其中 μ是均值，σ2 μ 是 均 值 ， σ 2 是标准差， ε ε 是用来控制分母为正。

但是数据本来不是这样子的啊！我们强行对数据进行缩放，可能是有问题的，所以BN又加了一个scale的操作，使得数据有可能会恢复回原来的样子：

yi=γx′i+β y i = γ x i ′ + β

加了scale可以提升模型的容纳能力。

既然是Batch归一化，那么BN就会受到batch size的影响：
1）如果size太小，算出的均值和方差就会不准确，影响归一化，导致性能下降

2）如果太大，内存可能不够用。

参考文章：https://zhuanlan.zhihu.com/p/36101196