RNN-GRU-LSTM详解
RNN-GRU-LSTM
- RNN（Recurrent Neural Network）
- GRU (gated recurrent unit)
- LSTM（Long short term memery）
- LSTM 能解决梯度消失/梯度爆炸？
RNN（Recurrent Neural Network）
卷积网络已经如此强大了，为何需要RNN呢？
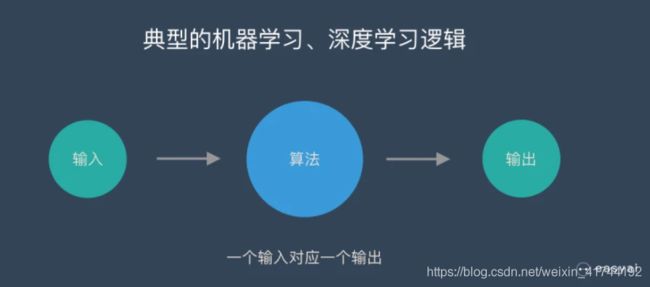
CNN 和普通的算法大部分一样，一个输入得到一个输出。不同的输入之间是没有联系的。
但是在某些场景中，一个输入就不够了！例如：为了填好下面的空，取前面任何一个词都不合适，我们不但需要知道前面所有的词，还需要知道词之间的顺序。
其他的还有：
文章里的文字内容
语音里的音频内容
股票市场中的价格走势
…
这种需要处理「序列数据 – 一串相互依赖的数据流」的场景就需要使用 RNN 来解决了。
RNN 之所以能够有效的处理序列数据，主要是基于他的比较特殊的运行原理。下面给大家介绍一下 RNN 的基本运行原理。
RNN 的基本原理
传统神经网络的结构比较简单：输入层 – 隐藏层 – 输出层。如下图所示：
RNN 跟传统神经网络最大的区别在于每次都会将前一次的输出结果，带到下一次的隐藏层中，一起训练。如下图所示：
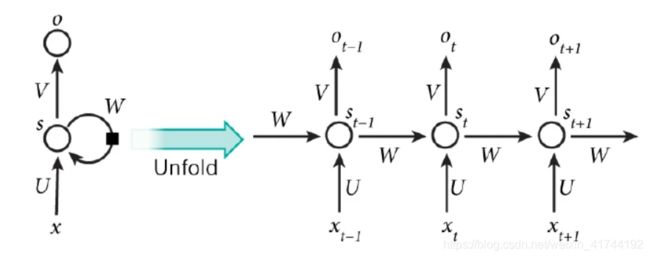
常见的论文多用这种折叠的模型：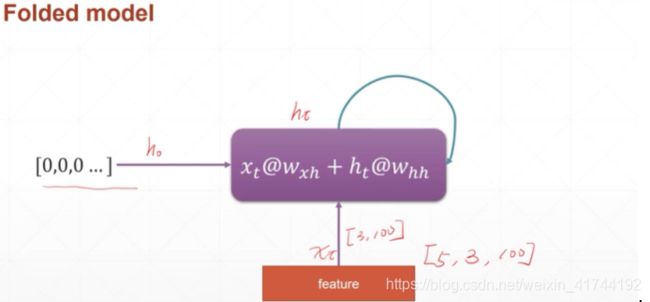
也可以拆开后这样理解：
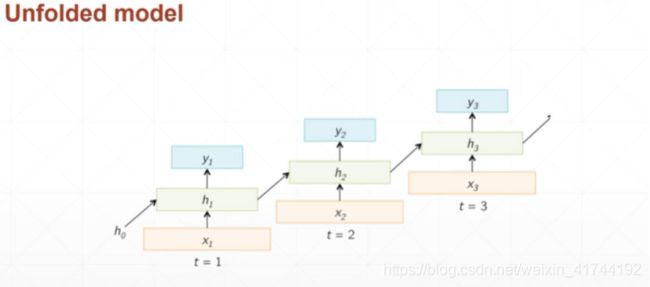
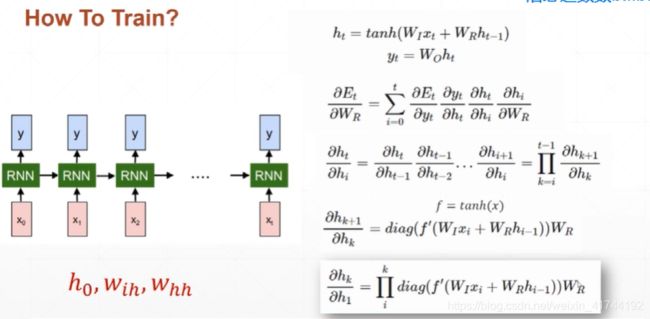
前向传播过程：
如上图所示，为RNN模型结构，前向传播过程包括：
训练过程中的反向传播：
下面用一个具体的案例来看看 RNN 是如何工作的：
假如需要判断用户的说话意图（问天气、问时间、设置闹钟…），用户说了一句“what time is it？”我们需要先对这句话进行分词：
然后按照顺序输入 RNN ，我们先将 “what”作为 RNN 的输入，得到输出「01」
然后，我们按照顺序，将“time”输入到 RNN 网络，得到输出「02」。
这个过程我们可以看到，输入 “time” 的时候，前面 “what” 的输出也产生了影响（隐藏层中有一半是黑色的）。
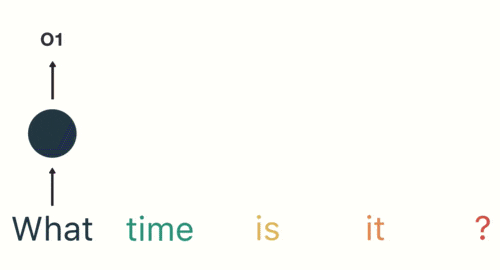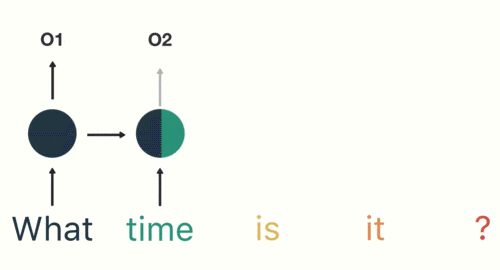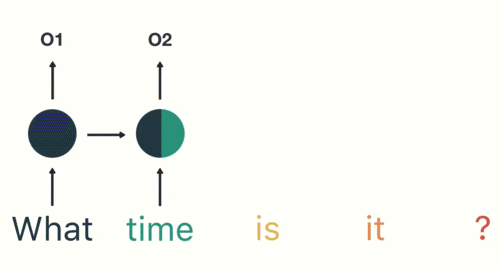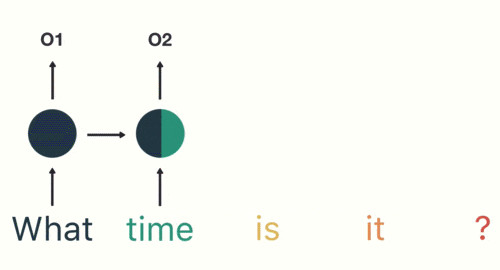
以此类推，前面所有的输入都对未来的输出产生了影响，大家可以看到圆形隐藏层中包含了前面所有的颜色。如下图所示：
当我们判断意图的时候，只需要最后一层的输出「05」，如下图所示：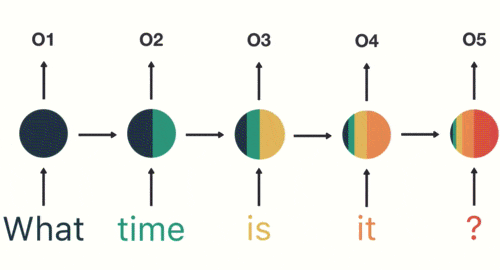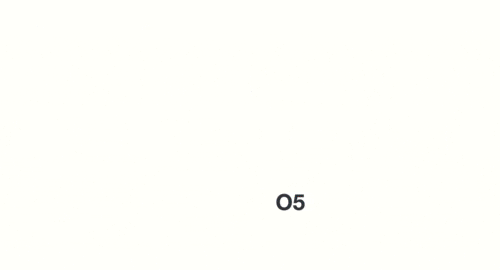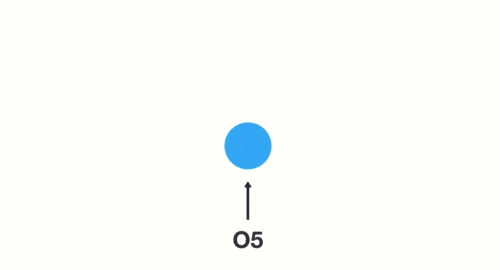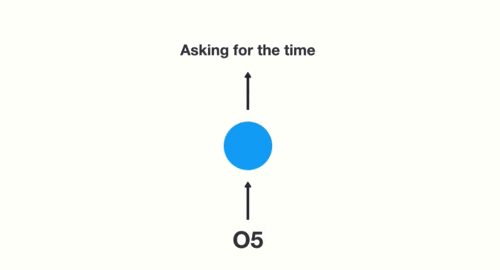
RNN 的缺点:
通过上面的例子，我们已经发现，短期的记忆影响较大（如橙色区域），但是长期的记忆影响就很小（如黑色和绿色区域），这就是 RNN 存在的短期记忆问题。
需要注意的是，RNN和DNN梯度消失和梯度爆炸含义并不相同。RNN中权重在各时间步内共享，最终的梯度是各个时间步的梯度和。因此，RNN中总的梯度是不会消失的，即使梯度越传越弱，也只是远距离的梯度消失。 RNN所谓梯度消失的真正含义是，梯度被近距离梯度主导，远距离梯度很小，导致模型难以学到远距离的信息。这才导致了 RNN 的短期记忆问题。 明白了RNN梯度消失的原因之后，我们看GRU和LSTM如何解决问题的呢？
GRU (gated recurrent unit)
GRU 旨在解决标准 RNN 中出现的梯度消失问题。GRU 也可以被视为 LSTM 的变体，因为它们基础的理念都是相似的，且在某些情况能产生同样出色的结果。如果读者希望了解 LSTM 与 GRU 的详细区别，可以查看论文 Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling。
GRU 原论文：https://arxiv.org/pdf/1406.1078v3.pdf
GRU 有两个有两个门，即一个重置门（reset gate）和一个更新门（update gate）。从直观上来说，重置门决定了如何将新的输入信息与前面的记忆相结合，更新门定义了前面记忆保存到当前时间步的量。如果我们将重置门设置为 1，更新门设置为 0，那么我们将再次获得标准 RNN 模型。使用门控机制学习长期依赖关系的基本思想和 LSTM 一致，但还是有一些关键区别：
- GRU 有两个门（重置门与更新门），而 LSTM 有三个门（输入门、遗忘门和输出门）。
- GRU 并不会控制并保留内部记忆（c_t），且没有 LSTM 中的输出门。
- LSTM 中的输入与遗忘门对应于 GRU 的更新门，重置门直接作用于前面的隐藏状态。
- 在计算输出时并不应用二阶非线性。
下面详细介绍GRU：
GRU 是标准循环神经网络的改进版，但到底是什么令它如此高效与特殊？
为了解决标准 RNN 的梯度消失问题，GRU 使用了更新门（update gate）与重置门（reset gate）。基本上，这两个门控向量决定了哪些信息最终能作为门控循环单元的输出。这两个门控机制的特殊之处在于，它们能够保存长期序列中的信息，且不会随时间而清除或因为与预测不相关而移除。
为了解释这个过程的机制，我们将具体讨论以下循环网络中的单元传递过程。
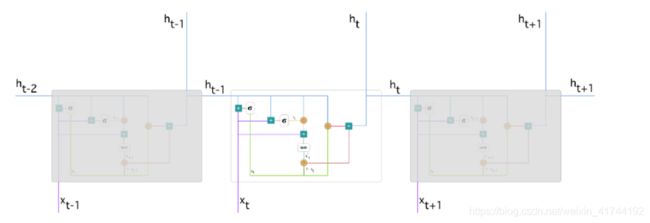
带有门控循环单元的循环神经网络
以下展示了单个门控循环单元的具体结构。
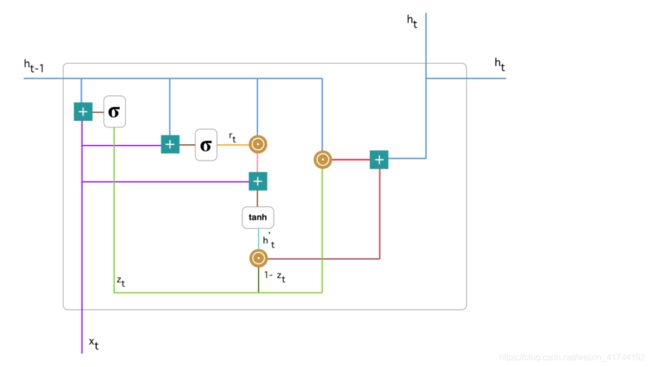
门控循环单元
首先我们需要指定以下符号：
1.更新门
在时间步 t，我们首先需要使用以下公式计算更新门 z_t：
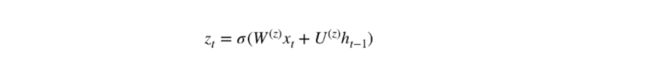
其中 x_t 为第 t 个时间步的输入向量，即输入序列 X 的第 t 个分量，它会经过一个线性变换（与权重矩阵 W(z) 相乘）。h_(t-1) 保存的是前一个时间步 t-1 的信息，它同样也会经过一个线性变换。更新门将这两部分信息相加并投入到 Sigmoid 激活函数中，因此将激活结果压缩到 0 到 1 之间。以下是更新门在整个单元的位置与表示方法。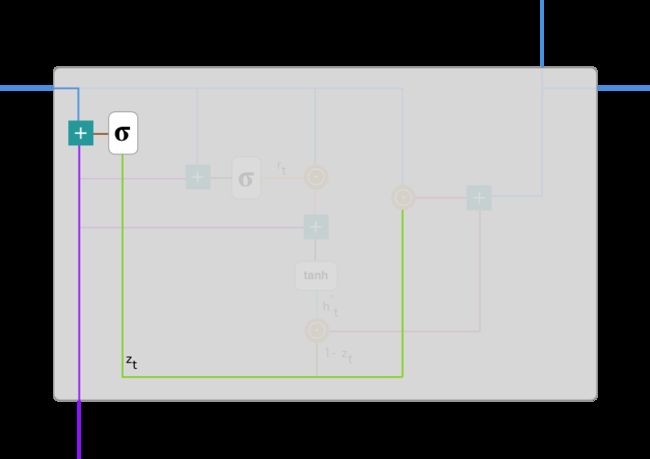
更新门帮助模型决定到底要将多少过去的信息传递到未来，或到底前一时间步和当前时间步的信息有多少是需要继续传递的。这一点非常强大，因为模型能决定从过去复制所有的信息以减少梯度消失的风险。我们随后会讨论更新门的使用方法，现在只需要记住 z_t 的计算公式就行。
- 重置门
本质上来说，重置门主要决定了到底有多少过去的信息需要遗忘，我们可以使用以下表达式计算：
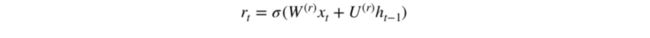
该表达式与更新门的表达式是一样的，只不过线性变换的参数和用处不一样而已。下图展示了该运算过程的表示方法。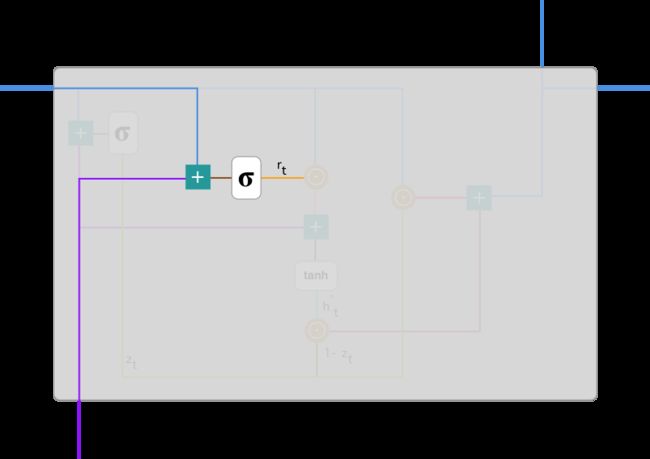
如前面更新门所述，h_(t-1) 和 x_t 先经过一个线性变换，再相加投入 Sigmoid 激活函数以输出激活值。 - 当前记忆内容
现在我们具体讨论一下这些门控到底如何影响最终的输出。在重置门的使用中，新的记忆内容将使用重置门储存过去相关的信息，它的计算表达式为：
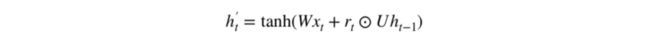
输入 x_t 与上一时间步信息 h_(t-1) 先经过一个线性变换，即分别右乘矩阵 W 和 U。
计算重置门 r_t 与 Uh_(t-1) 的 Hadamard 乘积，即 r_t 与 Uh_(t-1) 的对应元素乘积。因为前面计算的重置门是一个由 0 到 1 组成的向量，它会衡量门控开启的大小。例如某个元素对应的门控值为 0，那么它就代表这个元素的信息完全被遗忘掉。该 Hadamard 乘积将确定所要保留与遗忘的以前信息。
将这两部分的计算结果相加再投入双曲正切激活函数中。该计算过程可表示为：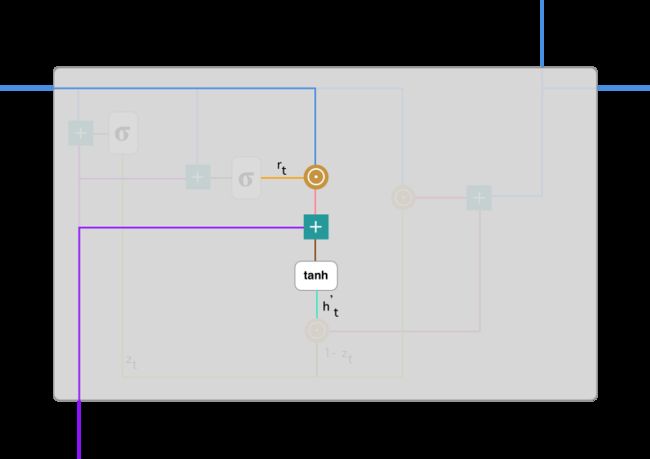
- 当前时间步的最终记忆
在最后一步，网络需要计算 h_t，该向量将保留当前单元的信息并传递到下一个单元中。在这个过程中，我们需要使用更新门，它决定了当前记忆内容 h’t 和前一时间步 h(t-1) 中需要收集的信息是什么。这一过程可以表示为：
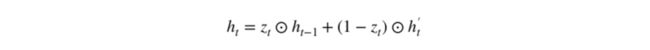
z_t 为更新门的激活结果，它同样以门控的形式控制了信息的流入。z_t 与 h_(t-1) 的 Hadamard 乘积表示前一时间步保留到最终记忆的信息，该信息加上当前记忆保留至最终记忆的信息就等于最终门控循环单元输出的内容。
以上表达式可以展示为：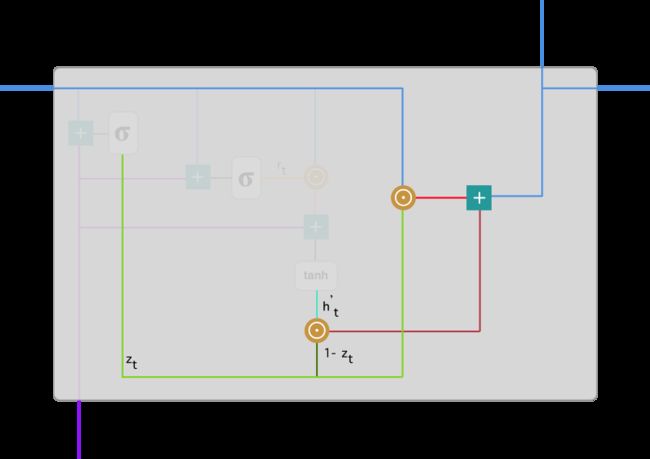
现在我们应该比较了解到底 GRU 是如何通过更新门与重置门存储并过滤信息。门控循环单元不会随时间而清除以前的信息，它会保留相关的信息并传递到下一个单元，因此它利用全部信息而避免了梯度消失问题。
LSTM（Long short term memery）
LSTM 的控制流程与 RNN 相似，它们都是在前向传播的过程中处理流经细胞的数据，不同之处在于 LSTM 中细胞的结构和运算有所变化。
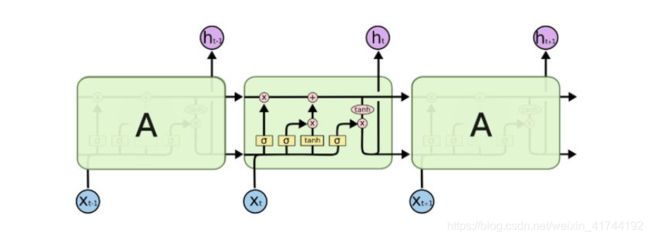如上图所示，为RNN门控结构，前向传播过程包括，
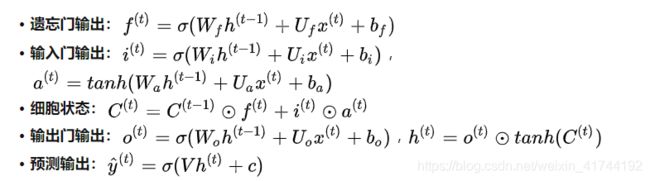
远距离梯度不至于完全消失，也就能够解决RNN中存在的"梯度消失"问题。LSTM虽然能够解决梯度消失问题，但并不能够避免梯度爆炸问题，仍有可能发生梯度爆炸。但是，由于LSTM众多门控结构，和普通RNN相比，LSTM发生梯度爆炸的频率要低很多。梯度爆炸可通过梯度裁剪解决。
LSTM遗忘门值可以选择在[0,1]之间，让LSTM来改善梯度消失的情况。也可以选择接近1，让遗忘门饱和，此时远距离信息梯度不消失。也可以选择接近0，此时模型是故意阻断梯度流，遗忘之前信息。
代码示例：
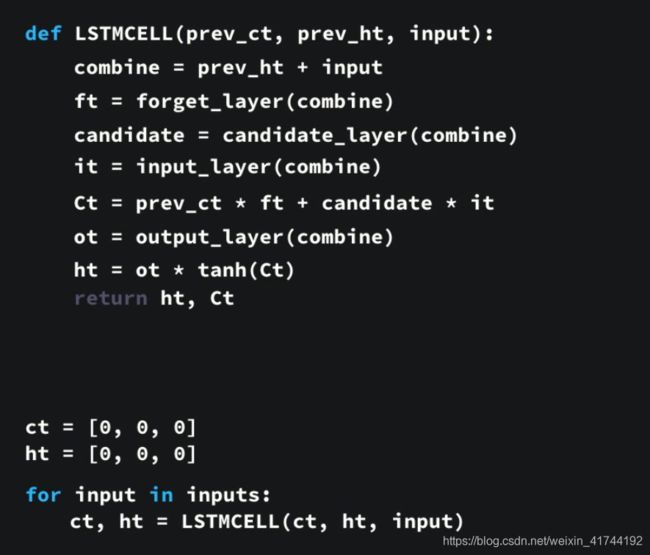
- 首先，我们将先前的隐藏状态和当前的输入连接起来，这里将它称为 combine；
- 其次将 combine 丢到遗忘层中，用于删除不相关的数据；
- 再用 combine 创建一个候选层，候选层中包含着可能要添加到细胞状态中的值；
- combine 同样要丢到输入层中，该层决定了候选层中哪些数据需要添加到新的细胞状态中；
- 接下来细胞状态再根据遗忘层、候选层、输入层以及先前细胞状态的向量来计算；
- 再计算当前细胞的输出；
- 最后将输出与新的细胞状态逐点相乘以得到新的隐藏状态。
LSTM 能解决梯度消失/梯度爆炸？
1、首先需要明确的是，RNN 中的梯度消失/梯度爆炸和普通的 MLP 或者深层 CNN 中梯度消失/梯度爆炸的含义不一样。MLP/CNN 中不同的层有不同的参数，各是各的梯度；而 RNN 中同样的权重在各个时间步共享，最终的梯度 g = 各个时间步的梯度 g_t 的和。
2、由 1 中所述的原因，RNN 中总的梯度是不会消失的。即便梯度越传越弱，那也只是远距离的梯度消失，由于近距离的梯度不会消失，所有梯度之和便不会消失。RNN 所谓梯度消失的真正含义是，梯度被近距离梯度主导，导致模型难以学到远距离的依赖关系。
3、LSTM 中梯度的传播有很多条路径， 这条路径上只有逐元素相乘和相加的操作，梯度流最稳定；但是其他路径（例如 ）上梯度流与普通 RNN 类似，照样会发生相同的权重矩阵反复连乘。
4、LSTM 刚提出时没有遗忘门，或者说相当于 ，这时候在 直接相连的短路路径上， 可以无损地传递给 ，从而这条路径上的梯度畅通无阻，不会消失。类似于 ResNet 中的残差连接。
5、但是在其他路径上，LSTM 的梯度流和普通 RNN 没有太大区别，依然会爆炸或者消失。由于总的远距离梯度 = 各条路径的远距离梯度之和，即便其他远距离路径梯度消失了，只要保证有一条远距离路径（就是上面说的那条高速公路）梯度不消失，总的远距离梯度就不会消失（正常梯度 + 消失梯度 = 正常梯度）。因此 LSTM 通过改善一条路径上的梯度问题拯救了总体的远距离梯度。
6、同样，因为总的远距离梯度 = 各条路径的远距离梯度之和，高速公路上梯度流比较稳定，但其他路径上梯度有可能爆炸，此时总的远距离梯度 = 正常梯度 + 爆炸梯度 = 爆炸梯度，因此 LSTM 仍然有可能发生梯度爆炸。不过，由于 LSTM 的其他路径非常崎岖，和普通 RNN 相比多经过了很多次激活函数（导数都小于 1），因此 LSTM 发生梯度爆炸的频率要低得多。实践中梯度爆炸一般通过梯度裁剪来解决。
7、对于现在常用的带遗忘门的 LSTM 来说，6 中的分析依然成立，而 5 分为两种情况：其一是遗忘门接近 1（例如模型初始化时会把 forget bias 设置成较大的正数，让遗忘门饱和），这时候远距离梯度不消失；其二是遗忘门接近 0，但这时模型是故意阻断梯度流的，这不是 bug 而是 feature（例如情感分析任务中有一条样本 “A，但是 B”，模型读到“但是”后选择把遗忘门设置成 0，遗忘掉内容 A，这是合理的）。当然，常常也存在 f 介于 [0, 1] 之间的情况，在这种情况下只能说 LSTM 改善（而非解决）了梯度消失的状况。
8、最后，别总是抓着梯度不放。梯度只是从反向的、优化的角度来看的，多从正面的、建模的角度想想 LSTM 有效性的原因。
参考文献：
- Written Memories: Understanding, Deriving and Extending the LSTM
- Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling
- https://www.zhihu.com/question/34878706
- https://zhuanlan.zhihu.com/p/136223550
- https://www.jiqizhixin.com/articles/2017-12-24