SLAM基础——常见矩阵以及矩阵分解
0 前言
本篇,多出自其他大佬的文章,厚着脸皮总结组织一下
1 矩阵求解
参考链接
https://blog.csdn.net/wangshuailpp/article/details/80209863
https://www.cnblogs.com/AndyJee/p/3846455.html
https://blog.csdn.net/wangshuailpp/article/details/80209863
https://www.cnblogs.com/AndyJee/p/3846455.html
1-1 内容一:直接给出 A X = B \bf{AX=B} AX=B解的情况。
(1)R(A)< r(A|B),方程组无解
(2)r(A)=r(A|B)=n,方程组有唯一解
(3)r(A)=r(A|B) < n,方程组有无穷解
(4)r(A)>r(A|B),这种情况不存在
其中r()代表矩阵的秩,A|B是增广矩阵,n是X未知数个数。
- 当A满秩时,为了提高效率通常采用QR分解、LTLD分解、Cholesky分解和SVD分解(奇异分解)等。
- 当A亏秩时,只能使用SVD分解方法,其他方法将失效。
QR分解?LTLD分解、Cholesky分解、SVD分解?
1-2 内容二:线性最小二乘问题
min ∥ A x − b ∥ 2 2 A ∈ R m ∗ n x ∈ R n b ∈ R m \min \|A x-b\|_{2}^{2} \\ A \in R^{m^{*} n} \quad x \in R^{n} \quad b \in R^{m} min∥Ax−b∥22A∈Rm∗nx∈Rnb∈Rm
m个方程求解n个未知数,有三种情况:
- m = n \mathrm{m}=\mathrm{n} m=n 且A为非奇异, 则有唯一解, x = A − 1 b x=A^{-1} b x=A−1b
- m > n m>n m>n, 约束的个数大于未知数的个数, 称为超定问题 (overdetermined)
- m < n \mathrm{m}<\mathrm{n} m<n, 负定/欠定问题 (underdetermined)
通常我们遇到的都是超定问题, 此时A = = = b的解是不存在的,从而转向解最小二乘问题: f ( x ) = ∥ A x − b ∥ f(x)=\|A x-b\| f(x)=∥Ax−b∥ ,其中 f ( x ) \mathrm{f}(\mathrm{x}) f(x) 为凸函数。令一阶导数为 0, 得到: A T A x − A T b = 0 A^{T} A x-A^{T} b=0 ATAx−ATb=0,称之为正规方程
一般解: x = ( A T A ) − 1 A T b x=\left(A^{T} A\right)^{-1} A^{T} b x=(ATA)−1ATb可见一般在视觉SLAM中后端优化就是约束项大于未知数的个数(超定问题), 采用最小二乘问题求 解
2 SLAM中常用的矩阵
2-1 正交矩阵
1.正交矩阵
矩阵和它的转置矩阵的乘积为单位矩阵,, 那么这个矩阵就是正交矩阵。李群中旋转矩阵就是一种正交阵,所以一般其逆的形式直接写成转置。
M T M = I ⟺ M T = M − 1 \mathbf{M}^{T} \mathbf{M}=\mathbf{I} \Longleftrightarrow \mathbf{M}^{T}=\mathbf{M}^{-1} MTM=I⟺MT=M−1
为什么叫正交矩阵呢?因为如果我们把这个矩阵写成向量的形式, 那么这些向量除了自己和自己的点积为1,其他任意两个不同向量之间的点积全部为0.而向量点积为0的情况叫正交。正交矩阵是因此得名的
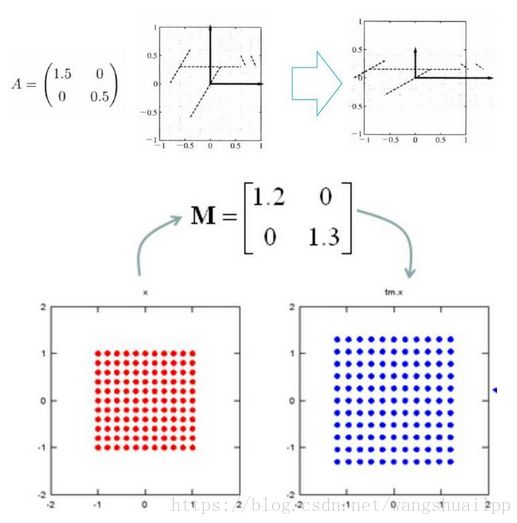
2-2 对角矩阵
乘以一个对角矩阵,好比对每个坐标轴进行缩放,包括方向,和压缩。
- 正数的乘法:正数好比在原方向上的缩放, 大于1,表示伸长,小于1,表示缩小。
- 零的乘法:零表示空间压缩。
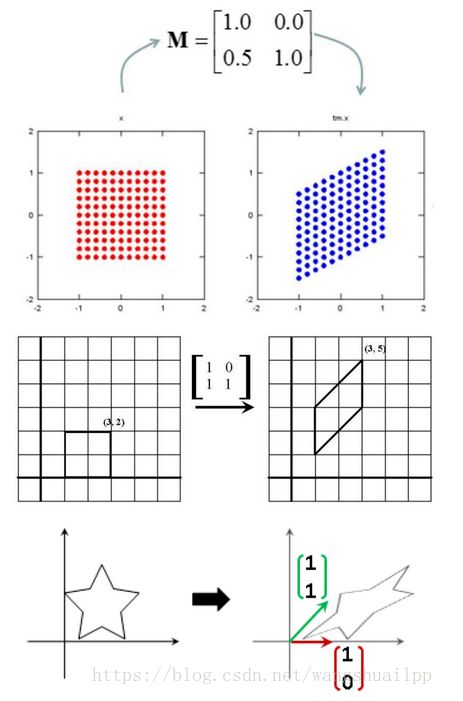
2-3 三角矩阵
和对角矩阵相比,三角矩阵要多一些角上的元素,那么这些元素有什么作用呢?
- 上三角矩阵:上三角矩阵的作用好比进行右上的切变,水平的斜拉。
- 下三角矩阵:同样是切边,不过是往左下切边,垂直方向的下拉
2-4 总结
矩阵分解就是分解成上面三种形式,综上所述,矩阵分解的几何意义就是把一个线性变换分解开来,分别是缩放,切边和旋转。矩阵因子的作用就是要把缩放,切边和旋转分解出来理解一个矩阵的作用。
3 矩阵分解
- 当A亏秩时,只能使用SVD分解方法,其他方法将失效
- LDLT只针对对称矩阵
3-1 QR分解
QR分解介绍
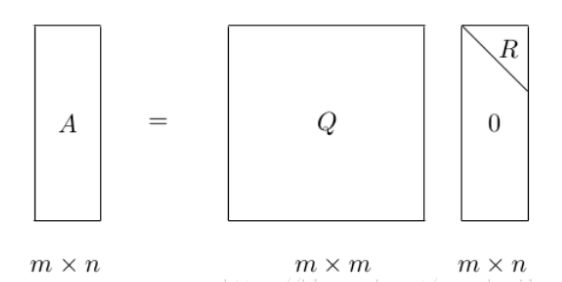
当A是非奇异的实方阵(满秩,只有方阵才存在奇异性,奇异矩阵秩亏,行列式为0,非奇异矩阵满秩,行列式不为0),实方阵A能够表示成一个正交矩阵Q(QTQ=I)与上三角矩阵R的积。
QR分解的实际计算有很多方法,例如 Givens 旋转、Householder 变换,以及 Gram-Schmidt正交化等等。A=Q*R称为A的QR分解。如下图所示
正交矩阵可以看成是坐标系的转换。从几何上QR分解,就是先进行旋转,然后再进行切变的过程。
QR分解满秩最小二乘问题
设 A A A 有 QR 分解:
A = Q ( R 0 ) = Q 1 R A=Q\left(\begin{array}{l} R \\ 0 \end{array}\right)=Q_{1} R A=Q(R0)=Q1R
其中Q是正交矩阵, Q 1 \bf{Q_{1}} Q1是 Q \bf {Q} Q的前n列组成的矩阵,R是对角线上元素均为正数的上三角矩阵。
由于正交矩阵保持范数不变, 所以等价于
∥ Q T ( A x − b ) ∥ 2 = min { ∥ Q T ( A v − b ) ∥ 2 : v ∈ R n } \left\|Q^{T}(A x-b)\right\|_{2}=\min \left\{\left\|Q^{T}(A v-b)\right\|_{2}: v \in R^{n}\right\} ∥∥QT(Ax−b)∥∥2=min{∥∥QT(Av−b)∥∥2:v∈Rn}
记
d = Q T b = ( Q 1 T Q 2 τ ) b = ( d 1 d 2 ) \boldsymbol{d}=Q^{T} \boldsymbol{b}=\left(\begin{array}{l} Q_{1}^{T} \\ Q_{2}^{\tau} \end{array}\right) \\ \boldsymbol{b}=\left(\begin{array}{l} \boldsymbol{d}_{1} \\ \boldsymbol{d}_{2} \end{array}\right) d=QTb=(Q1TQ2τ)b=(d1d2)
则有
∥ Q T ( A x − b ) ∥ 2 2 = ∥ ( R 0 ) x − ( d 1 d 2 ) ∥ 2 2 = ∥ R x − d 1 ∥ 2 2 + ∥ d 2 ∥ \left\|Q^{T}(A x-b)\right\|_{2}^{2}=\left\|\left(\begin{array}{l} R \\ 0 \end{array}\right) x-\left(\begin{array}{l} d_{1} \\ d_{2} \end{array}\right)\right\|_{2}^{2}=\left\|R x-d_{1}\right\|_{2}^{2}+\left\|d_{2}\right\| ∥∥QT(Ax−b)∥∥22=∥∥∥∥(R0)x−(d1d2)∥∥∥∥22=∥Rx−d1∥22+∥d2∥
因此, x \boldsymbol{x} x 是当且仅当方程 R x = d 1 R \boldsymbol{x}=\boldsymbol{d}_{1} Rx=d1 的解。所以 解可由上三角方程组 R x = d 1 R \boldsymbol{x}=\boldsymbol{d}_{1} Rx=d1 求得。
QR 分解方法的基本步骤如下:
- STEP 1: 求 A A A 的 QR 分解:
- STEP 2: 计算 d 1 = Q 1 T b \boldsymbol{d}_{1}=Q_{1}^{T} \boldsymbol{b} d1=Q1Tb :
- STEP 3: 解方程组 R x = d 1 R x=d_{1} Rx=d1 。
QR分解算力和稳定性分析
QR 分解方法比正规化方法有较好的数值稳定性, 并且计算结果比正规化方法要精确。
当然, Q R \mathrm{QR} QR 方法比正规化方法会付出更大的计算代价。
3-2 LDLT分解
LDLT分解介绍
对称矩阵A可以分解成一个下三角矩阵L(Lower下)和一个对角矩阵D(Diagonal对角线)以及一个下三角矩阵L的转置LT三个矩阵相乘的形式。如下式
A = L D L T = ( 1 0 0 L 21 1 0 L 31 L 32 1 ) ( D 1 0 0 0 D 2 0 0 0 D 3 ) ( 1 L 21 L 31 0 1 L 32 0 0 1 ) \mathbf{A}=\mathbf{L D L}^{\mathrm{T}}=\left(\begin{array}{ccc} 1 & 0 & 0 \\ L_{21} & 1 & 0 \\ L_{31} & L_{32} & 1 \end{array}\right)\left(\begin{array}{ccc} D_{1} & 0 & 0 \\ 0 & D_{2} & 0 \\ 0 & 0 & D_{3} \end{array}\right)\left(\begin{array}{ccc} 1 & L_{21} & L_{31} \\ 0 & 1 & L_{32} \\ 0 & 0 & 1 \end{array}\right) A=LDLT=⎝⎛1L21L3101L32001⎠⎞⎝⎛D1000D2000D3⎠⎞⎝⎛100L2110L31L321⎠⎞
由A的分解可知 A T = A \bf A^{T}=A AT=A,即A的转置等于A矩阵本身。所以,此方法针对对称矩阵
LDLT分解解满秩最小二乘问题
一般无法得到满足对称矩阵A,因此需要使对ATA(满足对称)进行分解。将求解问题转换成下面的式子:
A T A x = A T b A^{T} A x=A^{T} b ATAx=ATb
由于 r ( A ) = n \mathrm{r}(\mathrm{A})=\mathrm{n} r(A)=n, 所以 A T A \bf{A^{T}A} ATA是对称(正定)矩阵, 式子有唯一解, 使用LDLT分解的步骤是:
- STEP 1:定义矩阵 C = A T ⋆ A , d = A T ∗ b \mathrm{C}=\mathrm{AT}^{\star} \mathrm{A}, \mathrm{d}=\mathrm{AT}^{*} \mathrm{~b} C=AT⋆A,d=AT∗ b;
- STEP 2:对C进行cholesky分解 C = L D L T \mathrm{C}=\mathrm{L} \mathrm{D} \mathrm{L^{T}} C=LDLT, 原式变成 L D L T x = d \mathrm{L} \mathrm{D} \mathrm{L^{T}} \mathrm{x}=\mathrm{d} LDLTx=d
- STEP 3:令 y = L T x \mathrm{y}=\mathrm{L^{T}} \mathrm{x} y=LTx, 原式变成 L D y = d \mathrm{L} \mathrm{D} \mathrm{y}=\mathrm{d} LDy=d, 求解此方程得到y,然后求解 y = L T x \mathrm{y}=\mathrm{LTx} y=LTx得到 x \mathrm{x}_{\text { }} x
LDLT算力和稳定性分析
LDLT分解速度要快于QR分解。
3-3 Cholesky分解
Cholesky分解介绍
Cholesky分解是LDLT分解的一种特殊形式,也就是其中的D是单位矩阵。正定对称矩阵 A可以分解成一个下三角矩阵L和这个下三角矩阵L的转置LT相乘的形式。如下式
A = L L T = ( L 11 0 0 L 21 L 22 0 L 31 L 32 L 33 ) ( L 11 L 21 L 31 0 L 22 L 32 0 0 L 33 ) \mathbf{A}=\mathbf{L L}^{\mathbf{T}}=\left(\begin{array}{ccc} L_{11} & 0 & 0 \\ L_{21} & L_{22} & 0 \\ L_{31} & L_{32} & L_{33} \end{array}\right)\left(\begin{array}{ccc} L_{11} & L_{21} & L_{31} \\ 0 & L_{22} & L_{32} \\ 0 & 0 & L_{33} \end{array}\right) A=LLT=⎝⎛L11L21L310L22L3200L33⎠⎞⎝⎛L1100L21L220L31L32L33⎠⎞
Cholesky分解解满秩最小二乘问题
一般无法得到满足对称矩阵A,因此需要使对ATA(满足对称)进行分解。将求解问题转换成下面的式子:
A T A x = A T b A^{T} A x=A^{T} b ATAx=ATb
由于 r ( A ) = n \mathrm{r}(\mathrm{A})=\mathrm{n} r(A)=n, 所以 A T A \bf{A^{T}A} ATA是对称(正定)矩阵, 式子有唯一解, 使用LDLT分解的步骤是:
- STEP 1:定义矩阵 C = A T ⋆ A , d = A T ∗ b \mathrm{C}=\mathrm{AT}^{\star} \mathrm{A}, \mathrm{d}=\mathrm{AT}^{*} \mathrm{~b} C=AT⋆A,d=AT∗ b;
- STEP 2:对C进行cholesky分解 C = L L T \mathrm{C}=\mathrm{L} \mathrm{L^{T}} C=LLT, 原式变成 L L T x = d \mathrm{L} \mathrm{L^{T}} \mathrm{x}=\mathrm{d} LLTx=d
- STEP 3:令 y = L T x \mathrm{y}=\mathrm{L^{T}} \mathrm{x} y=LTx, 原式变成 L y = d \mathrm{L} \mathrm{y}=\mathrm{d} Ly=d, 求解此方程得到y,然后求解 y = L T x \mathrm{y}=\mathrm{LTx} y=LTx得到 x \mathrm{x}_{\text { }} x
Cholesky算力和稳定性分析
Cholesky分解要快于LDLT分解。
3-4 SVD分解(略,看自己关于SVD分解的笔记)
SVD分解不仅可以解决满秩最小二乘问题,最重要的是可以解决亏秩最小二乘问题(r(A)< n,理解下其实就相当于这里取r < n的情况),而前面的方法在秩亏的时候都会失效。