MapTR：Structured Modeling and Learning for Online Vectorized HD Map Construction——论文笔记

参考代码：MapTR

1. 概述

介绍：这篇文章提出了一种向量化高清地图（vectorized HD map）构建的方法，该方法将高清地图中的元素（线条状或是多边形的）构建为由一组点和带方向边的组合。由于点和方向边在起始点未知的情况下其实是能对同一地图元素够成很多种表达的，对此文章对一个元素穷举了其所有可能存在的等效表达并将其运用到的实例匹配中去，这样可以有效避免一些特意场景下的歧义情况（如对象车道中间的分割线或是人行横道的多边形区域 ）。直接预测一个地图元素对网络来说是很困难的，对此文中对其进行简化（引入层次匹配优化），也就是先通过拓扑结构匹配上地图元素，再去优化地图元素中的点和边得到准确预测结果。不过这篇文章给出的感知距离比较近范围大概为前后向各30米，文章也没有给出其在不同距离下的性能表现。

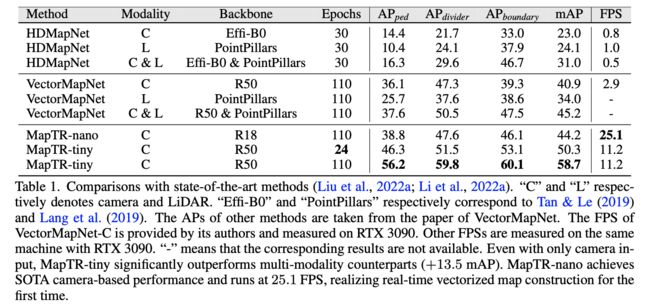
在之前的一些方法中会通过分割（HDMapNet）或是序列预测（VectorMapNet）形式对高清地图中的元素进行建模，分割的形式对后处理具有较强依赖，能够直接预测（end-to-end）高清地图元素的方法（如VectorMapNet）则更符合实际中对模型的需求。对VectorMapNet进行分析之后可知其在如下的场景下会发生定义歧义的情况：

也就是不知道如何定义元素的起点和方向，同时VectorMapNet使用的是序列预测的方法会导致误差积累，更长的训练和收敛时间。此外其infer时间也是需要考量的因素。

2. 方法设计

2.1 地图元素建模

对于地图中的元素文章将其描述为由一组有序点$V^F=[v_0,\dots ,v_{N_v-1}]$，$N_v$为元素中控制点的数目，这些点再与对应方向边组合便可得到对应地图元素表达。对于地图中的元素可以依据其几何拓扑结构可以将其划分为线形和多边形，那么元素中的点起点和边的朝向就有很多可能的情况，对此文章对一个地图元素采取穷举的方法进行表述，如下图所示：

对于一个地图元素$V^F$被建模为一组等效表达的集合$\mathcal{V}=(V,\Gamma )$，其中$\Gamma$就是这些点和方向穷举出来的等效元素表达。在文章的方法中将需要回归的目标通过transformer机制变为需要优化的query，以此实现最终结果预测。

2.2 训练时期的匹配机制

上文提到对于地图元素的建模是点和带方向边的组合，那么这些组合是如何与GT进行匹配的呢？文中指出其是通过两个层级的匹配实现的：instance层和point层，前一个用于确定大致回归目标，后一个用于精细化预测。见下图所示：

这里是采取1对多的形式建模，那么将其与固定顺序建模的结果进行比较：

2.2.1 instance层匹配

对于实例级别的匹配主要考虑两点：实例的类别和实例中点的位置差异：
$$L_{ins\_match}({\hat{y}}_{\pi (i)},y_i)=L_{Focal}({\hat{p}}_{\pi (i)},c_i)+L_{position}({\hat{V}}_{\pi (i)},V_i)$$
对于分类可以使用focal loss计算，对于实例的点则采用 point2point的方式计算，也即是对于集合中的点计算所有pair对的曼哈顿距离。对此文章也比较了两种不同实例点匹配方法：

则最佳的匹配就是代价最小的了：
$$\hat{\pi }=\underset{\pi \in {\prod }_N}{\mathrm{argmin}}\sum _{i=0}^{N-1}{L}_{ins\_match}({\hat{y}}_{\pi (i)},y_i)$$

2.2.2 point层匹配

这里点和点之间的匹配其实和上面instance匹配中点的匹配类似，也是通过穷举的方式计算距离差异：
$$\hat{\gamma }=\underset{\gamma \in \Gamma }{\mathrm{argmin}}\sum _{j=0}^{N_v-1}{D}_{Manhattan}({\hat{v}}_j,v_{\gamma }(j))$$
在得到匹配结果之后便是计算整体网络的损失，对于网络的损失是分为3个部分的：元素类的分类损失、配上元素中点的曼哈顿距离损失、点与点之间的朝向cosine损失。

此外，文中对于instance和point点分别用了不同query建模：

# projects/mmdet3d_plugin/maptr/dense_heads/maptr_head.py#L183
self.instance_embedding = nn.Embedding(self.num_vec, self.embed_dims * 2)
self.pts_embedding = nn.Embedding(self.num_pts_per_vec, self.embed_dims * 2)

在上文中提到对于地图元素的匹配过程是层次递进的，对应在query优化上也有借鉴，最后的query是两者的和：
$$q_{ij}^{(hie)}=q_i^{(ins)}+q_j^{(pt)}$$

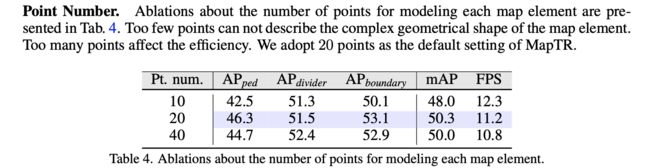
2.3 消融实验

文章的方法是在BEV场景下得到的，那么BEV特征的获取也是其需要关注的，下表对比了不同BEV特征构建方法的对比：

从上表中看出GKT的效果是最好的，在给出的代码中对GKT的实现做了一些改动，增加了query预测权重的部分。

对于地图元素中点的个数对性能的影响：

transformer解码器中层数对性能的影响：

3. 性能表现