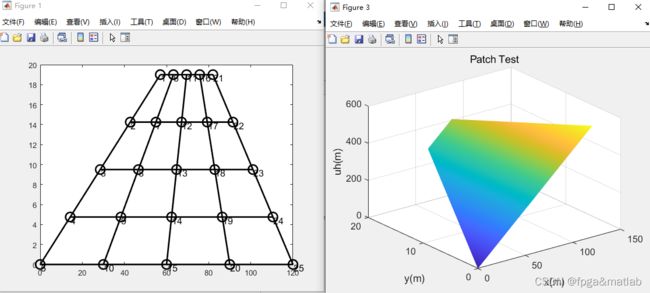
二维有限元的MATLAB仿真

%Xiamen University, FEM Class - Fall, 2006
%Patch test of 2D code

clear all; close all;
% Geometry properties for a rectangular shape
length = 10; height = 10;
% number of elements in each direction
ndivl = 4;
ndivw = ndivl;

% x,y:the coordinate of every node; node:the relationship of every node; numele;number of elements; total numnod:number of nodes
[x,y,x1,y1,node,numele,numnod] = fem2d_mesh(length,height,ndivl,ndivw);
y1=y1*1.9;
for i=1:ndivw+1
    A=y1(i,i);
    B=(120-(3+2)*A)/10;
    x1(i,:)=B*x1(i,:)+3*A;
end

for i = 1:(ndivl+1)
    for j=1:(ndivw+1)
        x((ndivw+1)*(i-1)+j) = x1(j,i);
        y((ndivw+1)*(i-1)+j) = y1(j,i);
    end
end
% Material properties

% Force and Displacement BC'S
[ifix,disp] = fem2d_ebcs(x,y,numnod,ndivl,ndivw);

% Construct Stifffness
ndof = 2;         %degrees of freedom per node
% Guass integration points and weights
ksi(1)=-1/sqrt(3); ksi(2)=1/sqrt(3);
weight(1)=1;       weight(2)=1;
% numequns:total number of equations; bigk:global stiffness; force:global force 
numeqns = numnod*ndof;
bigk = zeros(numeqns);
force = zeros(numeqns,1);

% Loop over elements
% nen is number of nodes per element
nen = 4;
for e = 1:numele
    % ke:element stiffness
    [ke] = fem2d_stiffness(node,x,y,ksi,weight,e);
    % assemble ke into bigk
    n1 = ndof-1;
    for i=1:nen;
        for j=1:nen;
            rbk = ndof*(node(i,e)-1) + 1;                  % row number of bigk
            cbk = ndof*(node(j,e)-1) + 1;                  % colunm number of bigk
            rbk1 = ndof*node(i,e);                  % row number of bigk
            cbk1 = ndof*node(j,e);                  % colunm number of bigk
            
            re = ndof*(i-1)+1;                             % row number of ke
            ce = ndof*(j-1)+1;                             % colunm number of ke
            re1 = ndof*i;                             % row number of ke
            ce1 = ndof*j;                             % colunm number of ke
            
            bigk(rbk:rbk+n1, cbk:cbk+n1) = bigk(rbk:rbk+n1, cbk:cbk+n1) + ke(re:re+n1, ce:ce+n1);
        end
    end
end

% Apply zero essential boundary conditions
for n=1:numnod
    if (ifix(n) == 1)
       force(:) = force(:) - disp(2*n-1)*bigk(:,2*n-1);
       bigk(2*n-1,:) = 0;
       bigk(:,2*n-1) = 0;
       bigk(2*n-1,2*n-1) = 1.0;
       
       force(:) = force(:) - disp(2*n)*bigk(:,2*n);
       bigk(2*n,:) = 0;
       bigk(:,2*n) = 0;
       bigk(2*n,2*n) = 1.0;
    end
end
for n=1:numnod
    if (ifix(n) == 1)
        force(2*n) = disp(2*n);
        force(2*n-1) = disp(2*n-1);
    end
end

% Solve stiffness equations
disp = bigk\force;
% Put the x,y & disp into matrix, calculate the exact solution
for i=1:(ndivl+1)
    for j=1:(ndivw+1)
        xh(j,i) = x((i-1)*(ndivw+1)+j);
        yh(j,i) = y((i-1)*(ndivw+1)+j);
        ux(j,i) = disp(2*((i-1)*(ndivw+1)+j)-1);
        uy(j,i) = disp(2*((i-1)*(ndivw+1)+j));
    end
end

% plot mesh
figure
for i=1:numele
    plot(x(node([1:4,1],i)),y(node([1:4,1],i)),'k-o','linewidth',2,'markersize',12)
    hold on
end
for i=1:numnod
    text(x(i)+0.2,y(i)-0.3,[num2str(i)],'fontsize',12)
end

figure
surf(xh,yh,ux)
shading interp

title('Patch Test','fontsize',12)
xlabel('x(m)','fontsize',12);ylabel('y(m)','fontsize',12);zlabel('uh(m)','fontsize',12)
set(gca,'fontsize',12)

figure
surf(xh,yh,uy)
shading interp

title('Patch Test','fontsize',12)
xlabel('x(m)','fontsize',12);ylabel('y(m)','fontsize',12);zlabel('uh(m)','fontsize',12)
set(gca,'fontsize',12)

 

D142