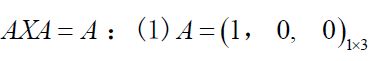【矩阵论】4. 矩阵运算——广义逆——加号逆应用

4.4.3 矩阵方程求解

前置：正规方程

a. 有解情况

若矩阵方程 $AXB=D$ 有解相容，则有特解 $X_0=A^{+}D{B}^{+}$

• 无解定理：若 $X_0=A^{+}D{B}^{+}$ ，使 $A{X}_{0}B\ne D$ ，则矩阵方程无解

• 齐次方程 $AXB=0$ 的通解公式为：$X=Y-A^{+}AYB{B}^{+}$ Y为任一矩阵

• 矩阵方程 $AXB=D$ 的通解公式为：$X=X_0+(Y-A^{+}AYB{B}^{+})=A^{+}D{B}^{+}+(Y-A^{+}AYB{B}^{+})$

$AXA=A$必有解,特解为 $X_0=A^{+}A{A}^{+}=A^{+}$，通解为 $X=X_0+(Y-A^{+}AYA{A}^{+})$

A有特解 $A_0=A^{+}={\left(1,0,0\right)}_{1\times 3}$ ，通解公式为 $X=A^{+}+(Y-A^{+}AYA{A}^{+})$ Y与 $A^{+}$ 同型即 $Y=Y_{1\times 3}$

令 $Y=(a,b,c)$ ,a,b,c为任意复数
$$\begin{array}{rl}& X=A^{+}+\left(a,b,c\right)-A^{+}A\left(a,b,c\right)A{A}^{+}\\ & =\left(1,0,0\right)+\left(a,b,c\right)-\left(a,0,0\right)=\left(1,b,c\right)\end{array}$$

---

解得：$X=(1,b,c{)}^T=\left(\begin{array}{c}1\\ b\\ c\end{array}\right)$ 即若 $AXA=A$ 有解，则 $A^T{X}^T{A}^T=A^T$ 有解

---

b. 无解情况

若矩阵方程 $AXB=D$ 无解，矩阵 $X=(x_{ij}{)}_{p\times q}$ 的欧式范数或模长记为 $\Vert X\Vert =\Vert X{\Vert }_F=\sqrt{\sum |x_{ij}{|}^2}=\sqrt{tr(X^{H}X)}$