【算法面试题汇总】LeetBook列表的算法面试题汇总---经典互联网公司的面试题目题目及答案

如果有错的还请各位大佬指出呀
有些是copy的还望不要介意
本人只做学习记录

只出现一次的数字

题目描述：

  给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

  说明：

    你的算法应该具有线性时间复杂度。 你可以不使用额外空间来实现吗？

示例：

输入: [2,2,1]
输出: 1

输入: [4,1,2,1,2]
输出: 4

• 代码实现

class Solution {
    public int singleNumber(int[] nums) {
        int value = 0;
        for(int i = 0;i<nums.length;i++){
            //任何数和0异或等于本身，任何数和自身异或等于0
            value = value ^ nums[i];
        }
        return value;
    }
}

• hashmap做法

class Solution {
    public int singleNumber(int[] nums) {
        int j = 0;
        Map<Integer,Integer> map = new HashMap<Integer,Integer>();
        //遍历该数组，往map集合里存，数组元素为key，出现次数为value
        for(int i = 0;i<nums.length;i++)
        {
            if(map.get(nums[i]) == null)
                map.put(nums[i],1);
            else 
                map.put(nums[i],map.get(nums[i]) + 1);    
        }
        //找出map集合里value为1的元素
        for (Map.Entry<Integer,Integer> str : map.entrySet()) { 
            if(str.getValue() == 1)
                j = str.getKey();
        }
        return j;
        }
    }
}

多数元素

题目描述：

  给定一个大小为 n 的数组 nums ，返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。

  你可以假设数组是非空的，并且给定的数组总是存在多数元素。

  尝试设计时间复杂度为 O(n)、空间复杂度为 O(1) 的算法解决此问题。

示例：

输入：nums = [3,2,3]
输出：3

输入：nums = [2,2,1,1,1,2,2]
输出：2

• 代码实现

class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        return nums[nums.length/2];
    }
}

搜索二维矩阵Ⅱ

题目描述：

  编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

  每行的元素从左到右升序排列。

每列的元素从上到下升序排列。

示例：

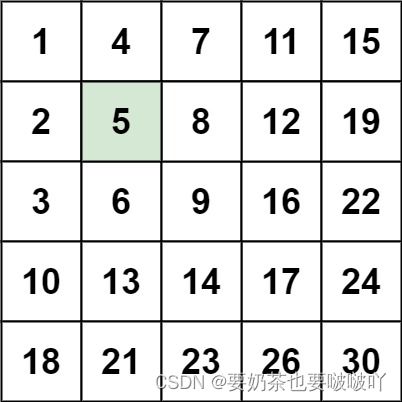
输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true

• 代码实现

class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        int row = matrix.length - 1;
        int col = matrix[0].length;
        int temp=0;

        while(row>=0 || temp<=col-1){
            if(matrix[row][temp] == target){
                return true;
            }else if(matrix[row][temp] < target){
                temp++;
                if(temp > col-1) return false;
            }else if(matrix[row][temp] > target){
                row--;
                if(row < 0) return false;
            }
        }
        return false;
    }
}

合并两个有序数组

题目描述：

  给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2，另有两个整数 m 和 n ，分别表示 nums1 和 nums2 中的元素数目。

  请你 合并 nums2 到 nums1 中，使合并后的数组同样按 非递减顺序 排列。

  注意：最终，合并后数组不应由函数返回，而是存储在数组 nums1 中。为了应对这种情况，nums1 的初始长度为 m + n，其中前 m 个元素表示应合并的元素，后 n 个元素为 0 ，应忽略。nums2 的长度为 n 。

示例：

输入：nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3
输出：[1,2,2,3,5,6]
解释：需要合并 [1,2,3] 和 [2,5,6] 。
合并结果是 [1,2,2,3,5,6] ，其中斜体加粗标注的为 nums1 中的元素。

• 代码实现

class Solution {
    public void merge(int[] nums1, int m, int[] nums2, int n) {
        int i=m-1;
        int j=n-1;
        int k=m+n-1;
        while(i>=0 && j>=0){
            if(nums1[i] > nums2[j]){
                nums1[k--] = nums1[i--];
            }else {
                nums1[k--] = nums2[j--];
            }
        }
        //nums2剩余的，nums1有剩余不用管，因为本来就是有序的
        while(j>=0){
            nums1[k--] = nums2[j--];
        }
        
    }
}

鸡蛋掉落

问题描述：

  给你 k 枚相同的鸡蛋，并可以使用一栋从第 1 层到第 n 层共有 n 层楼的建筑。

  已知存在楼层 f ，满足 0 <= f <= n ，任何从 高于 f 的楼层落下的鸡蛋都会碎，从 f 楼层或比它低的楼层落下的鸡蛋都不会破。

  每次操作，你可以取一枚没有碎的鸡蛋并把它从任一楼层 x 扔下（满足 1 <= x <= n）。如果鸡蛋碎了，你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎，则可以在之后的操作中 重复使用 这枚鸡蛋。

  请你计算并返回要确定 f 确切的值 的 最小操作次数 是多少？

示例：

输入：k = 1, n = 2
输出：2
解释：
鸡蛋从 1 楼掉落。如果它碎了，肯定能得出 f = 0 。 
否则，鸡蛋从 2 楼掉落。如果它碎了，肯定能得出 f = 1 。 
如果它没碎，那么肯定能得出 f = 2 。 
因此，在最坏的情况下我们需要移动 2 次以确定 f 是多少。

• 代码实现

class Solution {
    public int superEggDrop(int k, int n) {
        int[] dp = new int[k+1];
        int ans = 0;//操作次数
        while(dp[k]<n){
            for(int i=k;i>0;i--){
                //dp[k][f]=dp[k-1][f-1]+dp[k][f-1]+1
                //第f操作只和第f-1有关，所以用一维数组便可
                dp[i] = dp[i] + dp[i-1]+1;
            }
            ans++;
        }
        return ans;
    }
}