你所能用到的无损压缩编码（一）

      这个系列将结合C/C++介绍无损压缩编码的实现，正如Charles Petzold在<CODE:Hidden Language of Computer Hardware and Software>里所表达出来的意思一样，计算机最本质的能力就是将各种信息通过电路的开合转换成为一系列的数字，然后对其按照一定的规则进行编码，利用这些编码记录一些动作或者数据，完成人们想要的功能。计算机的指令是一种编码，数据也是一种编码，正如人类用各自民族特有的符号组成自己的语言一样，计算机也是依靠着编码形成了自己的语言。计算机的需要存储大量的数据，虽然现在的硬盘已经容量越来越大，但是如何存储更多的内容永远是计算机科学家不断追求的一个方向，压缩编码就像语言中的简称一样，使用尽量少的空间来存储和表达完整或者重要的信息。比如在日常生活中你会把电子计算机简称为计算机，本来五个字的内容现在只要三个字表达，但是完全没有改变其所表达的意思，这也是一种压缩。

     压缩编码是一种在计算机中常用的技术，在现代的电脑中基本无处不在，特别是在现在电脑中存储有大量的图片，视频的情况下，压缩编码几乎运用于所有格式的多媒体信息中，使得电脑可以更多的存储大量丰富的多媒体信息。人们根据从压缩编码中是否能完整无误的恢复出原始信息，又将压缩编码分成无损压缩和有损压缩两种，无损压缩就是可以通过压缩之后内容完整无误的恢复出原始信息，而有损压缩不是说不能恢复出原始信息，而是能够部分的恢复出原始信息，而这恢复的信息一般都是重要的信息，所谓损失是损失的次要信息，广泛使用的JPEG格式图片所采用的算法就是一种有损压缩的方法，它利用图像本身相关性很强的性质将原始图像数据进行有损压缩之后，然后解压缩呈现给用户的还是能够看到比较完整的原始图像。截止到现在，已经有很多有损压缩和无损压缩编码技术，对于压缩编码的研究也一直是多媒体的一个研究热点。

     既然是介绍无损压缩编码，那么就从最简单的RLE开始，RLE 全称Run-Length Encoding，一个接受的比较光的是行程编码，首先，让我们看一下RLE在Wiki中的定义：

     Run-length encoding (RLE) is a very simple form of data compression in which runs of data (that is, sequences in which the same data value occurs in many consecutive data elements) are stored as a single data value and count, rather than as the original run. This is most useful on data that contains many such runs: for example, simple graphic images suchas icons, line drawings, and animations. It is not useful with files that don't have many runs as it could greatly increase the file size.

     从定义中可以看出来，所谓的行程编码就是记录连续数据的行程(runs)长短和数值本身(data)，压缩之后的编码分成两组，value值和count值，value值就是连续出现的data值，count是其连续出现的次数。定义中也说了RLE对重复数据比较集中出现的数据压缩效果比较好，也就是行程长的数据，所以RLE主要应用于二值图像之中，如果相同数据连续出现的比较少，那么RLE压缩的效果将会很不理想，大部分情况下会越压缩越大。

     下面举个例子，比如000001111100000，使用RLE进行无损压缩之后是5 0 5 1 5 0， 可以看到本来使用15个数字的现在使用6个数字就能保存，大大减少了需要存储的数字的空间，这样也就是达到了压缩的目的。但是，反过来，如果数据是0101010101，那么使用RLE压缩后的结果就是1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1 1 0 1 1，本来只需要10个空间存储的数据，现在压缩之后变成了需要20个空间来存储，如果是1M的文件的话，那么压缩之后就变成2M。这也部分解释了为什么有时候使用压缩软件压缩文件，压缩之后的文件大小比原始文件大小还要大，所以压缩算法也不是完全就能实现压缩功能的，不光是对于RLE，对于大部分压缩算法，都有出现越压缩越大的可能。

     上面所叙述的都是压缩算法的原理，按照这些原理，就能编写出RLE压缩算法的程序，但是爱因斯坦说过： “ 从理论上说理论和实践是一回事，但是从实践上说他们不是一回事 ” ，所以在使用RLE压缩的时候，还要处理一个问题，先给大家展示下我的函数：

  

 1 //RLE压缩算法函数
 2 //输入:原始数据，原始信息长度，压缩数据
 3 //输出:压缩率
 4 double RLE(int input[],long inputLenth,int output[])
 5 {
 6     int count=1;//统计行程
 7     int j=0;
 8     for(int i=1;i<inputLenth;i++)
 9     {
10         //如果两个相邻的数据的值不同，记录下行程和数值，并重新初始化行程。
11         if(input[i]!=input[i-1])
12         {
13             output[j]=count;
14             output[j+1]=input[i-1];
15             count=1;
16             j+=2;
17         }
18         //如果两个相邻的数据的值相同，增加行程长度。
19         else
20         {
21             count++;
22         }
23         //对最后一个输入数据进行一些特殊处理
24         if(i==inputLenth-1)
25         {
26             output[j]=count;
27             output[j+1]=input[i];
28             j+=2;
29             output[j]=0;
30             
31         }
32         
33     }
34     return (double)j/(double)inputLenth;
35 }

       对于函数的说明见函数的注释，这里我需要特别说明的主要是两个方面：

       第一、正常情况下，用户是无法得知压缩之后的数据是多长的，所以你也无法预先设定输出数组的长度，这样会导致一个问题，在使用压缩数据时，也无法知道什么时候是压缩数据的结尾，如果这个问题不得到解决，那么将会导致在解压缩的时候得到不正确的结果，也就无法达到无损压缩的目的了，所以设计者在使用RLE时规定如果数据全部压缩结束，那么在结尾放上一个0，也就是采用一个0行程，因为正确数据压缩时，行程最小也是1，所以用0表示结束完美的解决了这个问题。

      第二，在处理原始数据最后一个数据的时候，可能会出现两种情况，倒数第一个数据和倒数第二个数据相同或者不相同，如果相同，那么行程就会加1，这样就导致了最后一组数据丢失，所以需要对最后一个数进行特殊处理，如果不同，那么会丢失最后一个数据，那么也会丢失最后一个数据，这也就是我的函数中最后一个if的含义。

      在此，我要说明的是，我的这个压缩函数只是一个粗略的版本，写出来之后也不愿意多细想，加上本人水平也有限，欢迎各位高手对我的函数提出改进意见。

      对于RLE压缩算法有了了解之后，解压缩其实很简单，将压缩之后的数据每一组每一组的读出来，第一个是数量，第二个是数值，然后按照规则进行恢复就可以了。下面是我的解压缩函数：

   

 1 //RLE解压缩算法函数
 2 //输入:压缩数据，压缩信息长度，原始数据
 3 void RLERecovery(int input[],int inputLenth,int output[])
 4 {
 5     int i=0;
 6     int count=0;
 7     while(i<inputLenth)
 8     {
 9        for(int j=0;j<input[i];j++)
10        {
11            output[j+count]=input[i+1];
12        }
13        //加上行程，保证输出数组的结果是正确的
14        count+=input[i];
15        i+=2; 
16     }
17  
18 
19 }

       由于RLE主要用于二值图像，所以在我们的函数中使用二值图像来测试我们的压缩算法和解压缩算法，测试图像如下：

      

       由于用的是二值图像，所以一个字节里有含有8个像素点，具体关于bmp图像的读写，请看我的上一篇和上上一篇日志，这里就不再详述，测试用的代码如下：

     

int _tmain(int argc, _TCHAR* argv[])
{
     
     //使用C里面的函数获得文件长度
     string fileName="inputtest.bmp";
     long length=GetFileLength(fileName);
 
     
     ofstream fout("output.txt",ios::binary);
     ifstream fin("inputtest.bmp",ios::binary);
     
     int inputValue;
      
 
     string str;
     int count=0;

     int *input=new int[length*8];
     //暂时将压缩后的数据长度设置和输入的一样，实际上有很多的浪费，由于不知道压缩后数据的长度
     int *output=new int[length*8];
     //读入图像数据
     while(getline(fin,str))
     {
         for(int i=0;i<str.length();i++)
         {
             for(int j=0;j<8;j++)
             {
                input[i*8+j+count]=(((unsigned char)str[i]>>j)&0x01);
             }
         }
         count+=str.length();
     
     }
     
     //输出压缩率并且进行压缩
     cout<<RLE(input,length*8,output)<<endl;
     
     //通过行程0判断已经压缩结束
     int j=0;
     while(j%2!=0||output[j]!=0)
     { 
         fout<<output[j]<<" ";
         j++;
     }
     //同时得到j就是压缩之后数据的长度
 
     
     fin.close();
     fout.close();
     
     /////////////////////////////////////////////////////////////////////////////////////////
     //解压缩过程
     ofstream newFout("outputtest.bmp",ios::binary);
     ifstream newFin("output.txt");
 
     //为了简便，就使用j作为压缩数组的长度
     int *newInput=new int[j];
     int *newOutput=new int[length*8];
     int k=0;
     while(!newFin.eof())
     {
        newFin>>newInput[k];
        k++;
     }
     
     //解压缩
     RLERecovery(newInput,j,newOutput);
     
     //将像素拼接，恢复原始数据恢复原始数据
     for(k=0;k<length*8;k+=8)
     {
          
         newFout<<(unsigned char)(newOutput[k+7]*128+newOutput[k+6]*64+newOutput[k+5]*32+newOutput[k+4]*16+newOutput[k+3]*8+newOutput[k+2]*4+newOutput[k+1]*2+newOutput[k]);
     } 
     cout<<endl;


    int i;
    cin>>i;
    
    return 0;
}

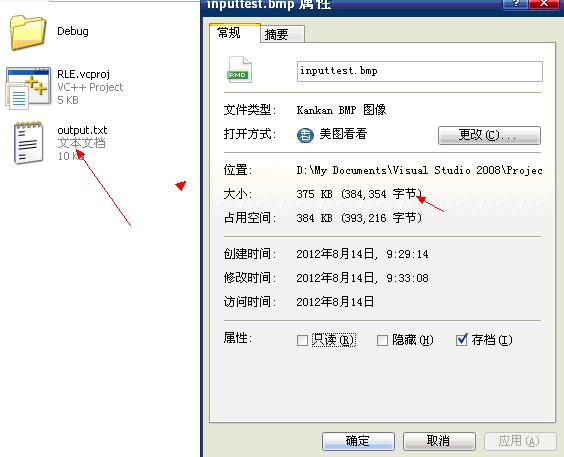
      输出后的压缩文件为一个10kb的文本文件，相比原始图像的375kb要小很多，而且你仍然可以再采用其余的编码和程序设计技巧使得这个数据大小更小，

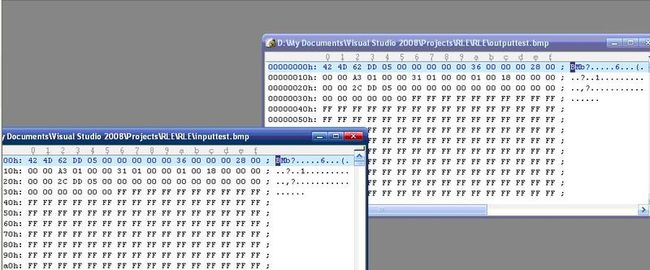
         你也可以通过输出压缩率的方式来看算法对某个文件的压缩效率，在解压缩方面，通过Ultra-edit，我们也可以看到，解压缩后的文件和原始文件一致的。

       

         在解压缩还原原始图像的时候，需要注意的就是“大端”和“小端”的问题，这个详细且有兴趣的话的可以见我前两篇文章。

         欢迎各位高手对代码以及文章提出意见。