【无标题】
推荐系统读书笔记(二):DisenKGAT——知识图谱解耦表征
收录会议:CIKM 2021
原文:https://arxiv.org/pdf/2108.09628.pdf
ABSTRACT
传统知识图谱补全方法单一、静态,不足以准确地捕获复杂关系。本文作者提出了一种新的解耦知识图谱注意网络(DisenKGAT),它利用微观解耦(新的关系感知聚合)和宏观解耦(利用互信息作为正则化来增强独立性)来挖掘知识图谱背后的表示,效果甚好。
KEYWORDS
知识图谱,图神经网络,解耦表示,互信息
1 INTRODUCTION
知识图谱补全(KGC),即基于知识图谱嵌入(KGE)方法,预测一个新的给定三元组是否有效。
传统模型忽略了有意义的图上下文信息,因此需要利用图卷积神经网络(分层传播来收集相邻实体嵌入)。
CompGCN将GCN的聚合与打分函数相结合,构建知识图补全中的编码器-解码器范式,但静态表示限制了嵌入的灵活性和表达能力,特别是在复杂的一对多(1-to-N)、多对一(N-to-1)和多对多(N-to-N)关系中。
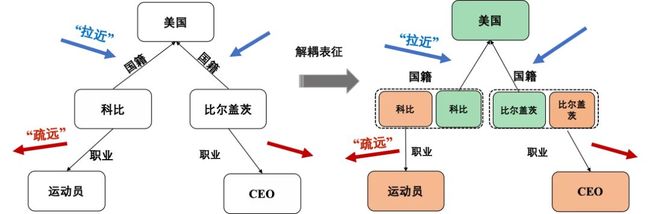
为啥静态表示有点整球不成?举个例子:
众所周知,“国籍”和“职业”都是一对多关系。科比(我怀疑论文作者有鞭尸的嫌疑)和比尔盖茨,一个是打篮球的,一个是开公司的,差了十万八千里。但就因为他俩都是米国人,使得“国籍”这一静态且唯一的表征,会显著影响图谱补全的效果,不能根据场景的动态变化生成不同的适应性表征。说通俗点就是,你说他俩在国籍上相似,但马上话题一变,聊职业了,你再谈国籍上的相似性,对不起不仅不管用了,还会干扰话题。
总结传统模型的劣势:
-
按理来说,同一实体在不同场景下应当展现出不同的表征含义,但传统模型简单粗暴地聚合邻域实体,无法有效地建模关键关系(邻居边信息往往蕴含着实际预测的场景)。
-
忽视了实体嵌入背后隐因子的耦合(其实就是把不同背景的属性邻居一锅炖),而一个实体可能有多个方面,各种关系集中在实体的不同方面。
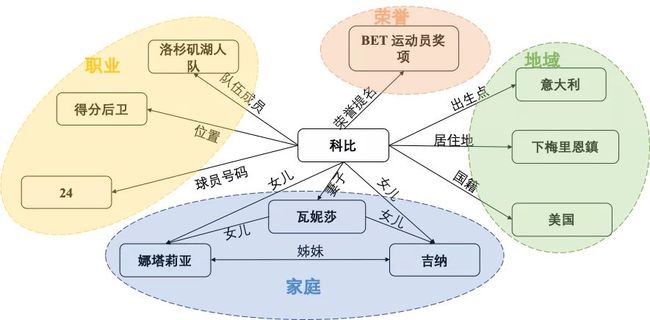
如下图所示,科比在不同场景下的信息都有邻接关系,比如职业、荣誉、家庭以及地域。假设问你关于科比的儿子信息,显然话题的重心是侧重于他家庭属性下的邻居,如他的妻子以及他的女儿,跟工作、荣誉这些属性扯不上半毛钱关系。
-
基于以上两点,这些方法的可解释性和鲁棒性较低,即容易对不符合当前情景的无关邻居产生过度反应,抹去KG本身丰富的结构和上下文信息。
本文作者通过引入基于解耦表征的学习框架以解决上述问题。
知识图谱解耦的核心思想为:通过将实体不同主题语义表示进行拆分解耦,根据给定查询针对性匹配相应主题化语义表示进行嵌入预测,以实现不同场景下动态化表示,从而有效解决复杂多语义知识图谱表示补全。
2 RELATED WORK
知识图谱嵌入(Knowledge Graph Embedding):以往的工作虽然用了花里胡哨的打分函数,对三元组预测效果比较好,甚至有的还搞了编码-解码来挖掘图谱,但都只考虑静态表示,没考虑到之前说的潜因子耦合问题
解耦表征学习(Disentangled Representation Learning):这部分人就比较聪明,发现了潜因子耦合——有的解耦了,但没完全解耦,搞了微观解耦(具体是啥后面解释),但没搞宏观;有的玩了独立正则和对抗学习,开拓了解耦学习的先河;还有的人专注于异构网络解耦……尽管如此,对于复杂的知识图仍然是一个挑战。
3 PRELIMINARY
3.1 知识图谱
G = { V , R , L } G = \{V, R, L\} G={V,R,L} ( V V V, R R R和 L L L表示实体节点集,关系集和边集)
对于一个从实体 h h h到实体 t t t的关系 r r r(即 h → r t h\overset{r}{\rightarrow} t h→rt),每条边 e ∈ L e∈L e∈L都代表一个三元组 ( h , r , t ) ∈ V × R × V (ℎ, r, t) ∈ V ×R ×V (h,r,t)∈V×R×V
举个煎蛋的栗子:h=我,t=CSDN,r=用户,e=(我,用户,CSDN)就表示我是CSDN的用户之一。
3.2 互信息
互信息(MI)是衡量两个随机变量相关性的基本量。
I ( X , Z ) = E ( p ( x , z ) ) [ l o g p ( x , z ) p ( x ) p ( z ) ] I (X, Z) = \mathbb{E}_{(p (x,z))} [log \frac{p(x, z)}{p(x)p(z)} ] I(X,Z)=E(p(x,z))[logp(x)p(z)p(x,z)]
其中, p ( x , z ) p(x,z) p(x,z)是随机变量 X X X和 Z Z Z的联合概率分布, p ( x ) p(x) p(x)和 p ( z ) p(z) p(z)为对应的边缘分布。
与传统相互关系相比,互信息能够捕获变量之间的非线性依赖关系,因此可以作为真正依赖关系的标准度量。
3.3 问题定义
给定一张残缺知识图谱,期望通过对其进行学习以实现残缺边的预测如给定头实体 h h h和边 r r r进行真实尾实体的预测 ( h , r , ? ) (h,r,?) (h,r,?) 。
现有任务往往是转变为一个排名任务,即期望通过打分函数 ψ ( h , r , t ) : V × R × V → R ψ(h,r,t):V×R×V→R ψ(h,r,t):V×R×V→R,对真实样本的预测情况优于负样本。
4 DISENTANGLED KNOWLEDGE GRAPH ATTENTION NETWORK
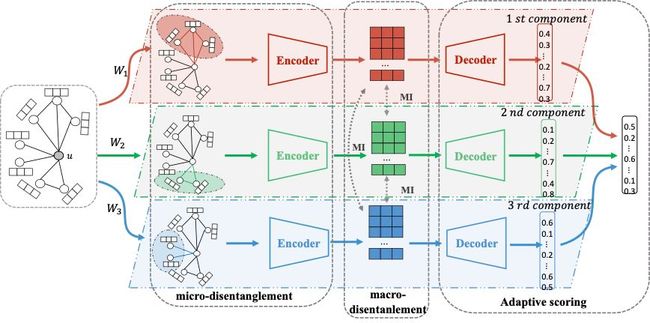
基于解耦表征学习的图谱补全框架如下图所示,整体模型包含三个关键部分:
-
微观解耦——关系感知信息聚合机制
-
宏观解耦——独立性限制
(解耦方法参照https://arxiv.org/abs/2103.07295)
-
动态打分预测——其中每种通道(颜色)代表一种特定的子部分信息,并且不同通道之间保持独立。最终的结果需要根据各通道的预测结果再根据当前场景与各通道的相似程度判断给出最终的预测分数排名。
4.1 解耦转换
本文提出的模型希望学习出的表征能够实现解耦,即每部分表征代表不同的含义。
具体来说,对于实体 u u u,本文假设它的表征由 K K K个独立因子共同决定,如 e u = [ h u , 1 , h u , 2 , ⋯ , h u , k ] e_u=[h_{u,1},h_{u,2},⋯,h_{u,k}] eu=[hu,1,hu,2,⋯,hu,k] ,其中 h u , k ∈ R d e m b e d K h_{u,k}∈\mathbb{R}^{\frac{d_{embed}}{K}} hu,k∈RKdembed ,表示实体 u u u在第 K K K部分的表征。
为了实现上述目标,首先将初始的实体表征向量 x u x_u xu映射到不同的隐空间当中,从而更好地帮助挖掘节点特征中的不同语义:
h u , k 0 = σ ( W k ⋅ x u ) ℎ^0_{u,k} = σ (W_k · x_u) hu,k0=σ(Wk⋅xu)
其中,实体的初始表征 { h u , k 0 } k = 1 K \{ℎ^0_{u,k} \}^K_{k=1} {hu,k0}k=1K是各实体表征通过 K K K 个独立的映射矩阵 W = { W 1 , W 2 , ⋯ , W K } W=\{W_1,W_2,⋯,W_K\} W={W1,W2,⋯,WK}得到的, σ σ σ是非线性激活函数, x u x_u xu是节点的特征。btw,没用正则,因为作者说没啥卵用(摊手手)
4.2 关系感知信息聚合(微观解耦)
回顾一哈GCN的传统艺能,为了全面地描述实体的各个组成部分,需要进行邻域聚合,以便每个实体的学习可以利用邻居信息丰富自己的嵌入表征。
再在其中加入解耦思想,我只想聚合与当前主题最为相关的部分邻居,并非所有邻居实体,那可以试试加权。还是拿科比的知识图谱举例(反复鞭尸),倘若给出查询其家庭信息,妻子、女儿等邻居应当赋予更高的权重。
因此,如何定义当前场景下最相关的邻居子集呢?与同构图中的邻居循迹策略不同的是,知识图谱中连接边的信息对主题的定义至关重要。因此要更好地实现解耦,在聚合过程中应当显式融入邻居边信息。
引入关系感知信息聚合机制——对于每个实体 u u u以及每个场景(子表征) k k k,进行以下交互以从特定邻居 v v v通过关系 r r r生成消息:
m ( v , k , r ) = ϕ ( h v , k , h r , θ r ) θ r = W r = d i a g ( w r ) m_{(v,k,r)} = ϕ (ℎ_{v,k}, ℎ_r, θ_r )\\ θ_r = W_r= diag(w_r ) m(v,k,r)=ϕ(hv,k,hr,θr)θr=Wr=diag(wr)
其中, ϕ : R d × R d × R d → R d ϕ:\mathbb{R}^d×\mathbb{R}^d×\mathbb{R}^d→\mathbb{R}^d ϕ:Rd×Rd×Rd→Rd 是一个信息融合操作; m ( v , k , r ) m(v,k,r) m(v,k,r) 代表着从邻居 v v v与边 r r r共同作用下聚合得到的信息; θ r ∈ R d θ_r ∈ \mathbb{R}^d θr∈Rd 表示关系特定的投影矩阵,并且沿用到后面的 s o f t m a x softmax softmax过程,以保证语义子空间的一致性(限制为对角矩阵,以提高效率);本文作者通过四种操作(减法、乘法、交叉作用与循环卷积)实现 ϕ ϕ ϕ。
为了更好地捕捉实体 u u u与实体 v v v之间关于子表征 k k k的相关性,作者提出一个关系感知注意力机制来衡量两实体该部分重要性程度。
这里同样为了简化操作,并且基于假设:即实体 u u u和邻居 v v v在关系 r r r方面在第 k k k个分量中越相似,二者在因子 k k k上越有可能建立联系。
采用点积(dot-product)注意力机制,具体表示如下(思想上沿用了KGAT里的衰减因子 π ( h , r , t ) π(h, r, t) π(h,r,t)):
α ( u , v , r ) k = s o f t m a x ( ( e u , r k ) T ⋅ e v , r k ) = e x p ( ( e u , r k ) T ⋅ e v , r k ) ∑ ( v ′ , r ) ∈ N ^ ( u ) e x p ( ( e u , r k ) T ⋅ e v ′ , r k ) α^k_{(u,v,r)} = softmax ({(e^k_{u,r} )}^T · e^k_{v,r} )\\=\frac{exp({(e^k_{u,r} )}^T · e^k_{v,r} )}{\sum_{(v',r)∈\hat{N}(u)}{exp({(e^k_{u,r} )}^T · e^k_{v',r} )}} α(u,v,r)k=softmax((eu,rk)T⋅ev,rk)=∑(v′,r)∈N^(u)exp((eu,rk)T⋅ev′,rk)exp((eu,rk)T⋅ev,rk)
其中, e u , r k = c u , k ◦ θ r e_{u,r}^k=c_{u,k}◦θ_r eu,rk=cu,k◦θr代表特定关系感知子空间中实体 u u u在第 k k k个关系感知分量的子表征; N ^ ( u ) \hat{N}(u) N^(u)表示 u u u的相邻实体及它自己所组成的集合;
得到注意力评分后,从邻居实体中聚合信息并且更新中心实体各子部分表征,用以下式子表示实体在通过$ l $层信息聚合后得到的最终表征分量:
h u , k l + 1 = σ ( ∑ ( v ′ , r ) ∈ N ^ ( u ) α ( u , v , r ) k ϕ ( h v , k l , h r l , θ r ) ) ℎ^{l+1}_{u,k} = σ ( \sum_{(v',r)∈\hat{N}(u)}α^k_{(u,v,r)} \phi(ℎ_{v,k}^l , ℎ_r^l, θ_r )) hu,kl+1=σ((v′,r)∈N^(u)∑α(u,v,r)kϕ(hv,kl,hrl,θr))
同样, h r l ℎ_r^l hrl表示关系 r r r在第 l l l层的表示形式,作者也用了一个权重矩阵 W r e l l W^l_{rel} Wrell来训练它。
总地来说,关系感知聚合策略让 h u , k l + 1 ℎ^{l+1}_{u,k} hu,kl+1倾向于聚合至一个较紧密的空间中,使得各部分相似语义表征相近,这就喊作微观解耦。
4.3 独立性限制(宏观解耦)
在复杂多关系图中(如知识图谱),我们期望不同语义空间中的子表征相互尽可能独立,即降低彼此直接依赖。
——>为此,之前的方法分别从距离相关性与希尔伯特-施密特独立性正则(HSIC)两个角度进行控制。
————但是(第一个但是)本文认为单纯控制线性相关无法满足复杂场景下的依赖关系,
————>因此,采用互信息这一衡量两个随机变量非线性相关性的基本量来控制,即最小化对不用语义间相关性进行控制。
——————但是(第二个但是)又由于高维度向量的互信息且无先验知识的情况下,无法计算出互信息的取值,
——————>于是,本文作者再次借助前辈的思想,采用一种对比对数比上界MI估计(contrastive log-ratio upper-bound MI estimator,好拗口)的方法来实现解耦。核心思想为借助对比正负样本之间的差异从而对互信息上界进行估计。
————————但是(第三个但是)该估计量不能直接应用于不同成分之间的条件概率,如 p ( h u , i ∣ h u , j ) ( i ≠ j ) p(ℎ_{u,i} |ℎ_{u,j} ) \ (i≠j) p(hu,i∣hu,j) (i=j)
————————>改进一哈,利用变分分布 q θ ( h u , i ∣ h u , j ) q_θ(ℎ_{u,i} |ℎ_{u,j} ) qθ(hu,i∣hu,j),用变分参数 θ θ θ建立一个简单的神经网络 Q Q Q来逼近真实的条件网络。
看完这一段,我的感慨:什么叫方法总比问题多啊(战术后仰)
最后定义损失函数为:
L m i = ∑ i ∑ j ( E ( h u , i , h u , j ) ∼ p ( h u , i , h u , j ) [ l o g q ( z u , i ∣ z u , j ) ] − E ( h u , i , h u ′ , j ) ∼ p ( h u , i , h u , j ) [ l o g q ( z u , i ∣ z u ′ , j ) ] ) L_{mi} = \sum _i \sum_j(\mathbb{E}_{(ℎ_{u,i},ℎ_{u,j} )∼p (ℎ_{u,i},ℎ_{u,j} ) }[log\ q(z_{u,i} |z_{u,j} )] \\\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ −\mathbb{E}_{(ℎ_{u,i},ℎ_{u',j} )∼p (ℎ_{u,i},ℎ_{u,j} ) }[log\ q(z_{u,i} |z_{u',j} )]) Lmi=i∑j∑(E(hu,i,hu,j)∼p(hu,i,hu,j)[log q(zu,i∣zu,j)] −E(hu,i,hu′,j)∼p(hu,i,hu,j)[log q(zu,i∣zu′,j)])
其中, Q Q Q用于同时训练以最小化真实条件概率 p ( h u , i ∣ h u , j ) ( i ≠ j ) p(ℎ_{u,i} |ℎ_{u,j} ) \ (i≠j) p(hu,i∣hu,j) (i=j)与变分条件概率 q θ ( h u , i ∣ h u , j ) q_θ(ℎ_{u,i} |ℎ_{u,j} ) qθ(hu,i∣hu,j)之间的KL散度。
L ( h u , i , h u , j ) = D K L [ p ( h u , i ∣ h u , j ) ∣ ∣ q θ ( h u , i ∣ h u , j ) ] L_{(ℎ_{u,i},ℎ_{u,j} )} = \mathbb{D}_{KL} [p(ℎ_{u,i} |ℎ_{u,j} )||q_θ(ℎ_{u,i} |ℎ_{u,j} )] L(hu,i,hu,j)=DKL[p(hu,i∣hu,j)∣∣qθ(hu,i∣hu,j)]
此处,假设条件分布 p ( h u , i ∣ h u , j ) p(ℎ_{u,i} |ℎ_{u,j} ) p(hu,i∣hu,j)为高斯分布,并用最终目标函数交替优化。
总结来说,通过上述操作可以实现不同语义空间能够捕捉到相似性尽可能小的语义。
将上述控制变量之间互信息即作为正则化项的方式称之为宏观解耦,它很大程度上保证了各语义空间都具有显著的代表性与独特性。
4.4 动态打分
解耦知识图谱表征的优点在于它的适应性,即各个方面对最终预测的重要性可以根据给定的场景(即知识图谱补全中的关系)进行自适应调整。
为了实现这一目标,在本模块作者首先先在每个语义表征分量里预测(Component-level prediction),然后利用一个注意力评分机制来指导来自不同语义空间结果的融合(Relation-aware attentive fusion)。
语义空间级预测
以尾实体预测为例。每当在 L L L次邻域聚合之后获得解耦的头实体和关系表示,就计算一次每个分量中每个候选三元组 ( u , r , v ) (u,r,v) (u,r,v)的分数。
可采用的打分函数有transE、DistMult和ConvE等等。以ConvE为例:
φ ( u , r , v ) k = f ( v e c ( f ( h u , k L ‾ ; h r L ‾ ★ ω ) ) W ) h v , k L φ^k_{(u,r,v)} = f(vec(f (\overline{h^L_{u,k}};\overline{h^L_r} ★ \omega))W )h^L_{v,k} φ(u,r,v)k=f(vec(f(hu,kL;hrL★ω))W)hv,kL
其中, h u , k L ‾ ∈ R d w × d h , h r L ‾ ∈ R d w × d h \overline{h^L_{u,k}}∈\mathbb{R}^{d_w×d_h},\overline{ℎ^L_r}∈\mathbb{R}^{d_w×d_h} hu,kL∈Rdw×dh,hrL∈Rdw×dh代表着原有的 h u , k L ∈ R d w d h × 1 , h r L ∈ R d w d h × 1 h^L_{u,k}∈\mathbb{R}^{d_wd_h×1},h^L_{r}∈\mathbb{R}^{d_wd_h×1} hu,kL∈Rdwdh×1,hrL∈Rdwdh×1重造后的 2D 表征结果;(★)为卷积操作。
整个公式用于衡量给定三元组 ( u , r , v ) (u,r,v) (u,r,v)在第 k k k个语义空间中的有效性预测概率。
关系感知融合
为了使本文模型能够适应于给定模型,作者在解码器部分之后加入了注意力评分模块 β ( u , r , v ) k β_{(u,r,v)}^k β(u,r,v)k
β ( u , r ) k = s o f t m a x ( ( h u , k L ◦ θ r ) T ⋅ h r L ) = e x p ( ( h u , k L ◦ θ r ) T ⋅ h r L ) ∑ k ′ e x p ( ( h u , k ′ L ◦ θ r ) T ⋅ h r L ) β_{(u,r)}^k = softmax ((h^L_{u,k} ◦ θ_r )^T ·h^L_r) = \frac{exp((h^L_{u,k} ◦ θ_r )^T ·h^L_r)}{\sum_{k'}exp((h^L_{u,k'} ◦ θ_r )^T ·h^L_r)} β(u,r)k=softmax((hu,kL◦θr)T⋅hrL)=∑k′exp((hu,k′L◦θr)T⋅hrL)exp((hu,kL◦θr)T⋅hrL)
假设在关系感知语义子空间当中,最佳匹配当前语义环境的语义表征应当更接近于该语义空间中连接边的表征。
举例来说(鞭尸梅开n度),对于残缺三元组(科比,球队队员,?)模型应当更多关注从“职业”主题相关的邻居中聚合邻近信息。
而职业主题邻居关系包含多个近似三元组,其中如(科比,球员号码,24)、(科比,位置,得分后卫)将相对于其他成分来说“更接近”于"运动队成员"的关系。因此,通过关系感知聚合模型共享语义映射矩阵 θ r θ_r θr ,可以彻底将不同语义子表征进行拆分,并且有效进行分离与计算。
最终预测结果:
φ ( u , r , v ) f i n a l = ∑ k β ( u , r ) k φ ( u , r , v ) k φ ^{final}_{(u,r,v)} = \sum_k β^k_{(u,r)} φ^k_{(u,r,v)} φ(u,r,v)final=k∑β(u,r)kφ(u,r,v)k
4.5 损失函数
在训练过程中,我们利用标准交叉熵损失和标签平滑,定义(地狱绘图)为:
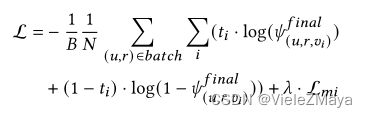
其中, B B B:批大小; N N N:KG中的实体数量; t i t_i ti是所给查询 ( u , r ) (u,r) (u,r)的标签; L m i L_{mi} Lmi和 λ \lambda λ:互信息正则化损失及其对应的超参数。
5 EXPERIMENTS
在本节中,作者通过实验来证明DisenKGAT的有效性。
-
RQ1:与现有的方法、基于距离的w.r.t.和语义匹配模型相比,DisenKGAT的表现如何?
-
RQ2:关键组分(如关系感知聚合)如何影响DisenKGAT,不同的超参数(如因子数)如何影响DisenKGAT?
-
RQ3: DisenKGAT与其他解码器模块是否可以粗略地工作?
-
RQ4: DisenKGAT能否解释分离因素带来的好处?
5.1 性能比较(RQ1)
-
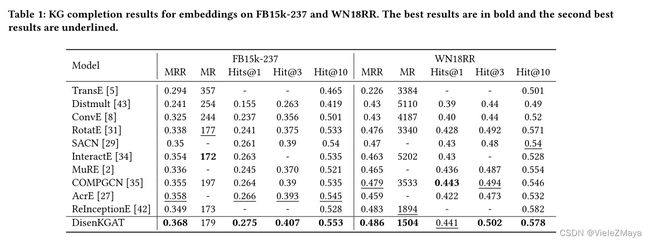
从表1的结果中,可以看到DisenKGAT与最先进的模型相比获得了具有竞争力的结果。
特别是,DisenKGAT在FB15k-237数据集的w.r.t MRR、Hits@1和Hits@3上取得了相当大的改进,也优于其他在WN18RR数据集上使用MR的模型。
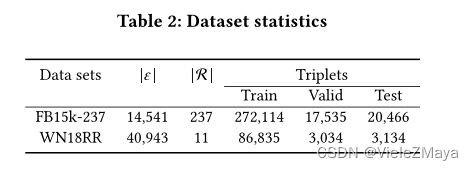
取得这样的结果归因于复杂知识图上的解耦模块。由于FB15k-237数据集包含237种关系类型,正好突出了模型适合于处理多关系纠缠问题的特点。
同时,WN18RR只包含11种关系类型,每个实体都包含一个极其单一的含义。例如,实体“pass on”有三种不同的含义(传输、转移占有、导致分发),每一种含义都属于一个单独的实体。因此,后面的实验将更多地关注FB15k-237。
-
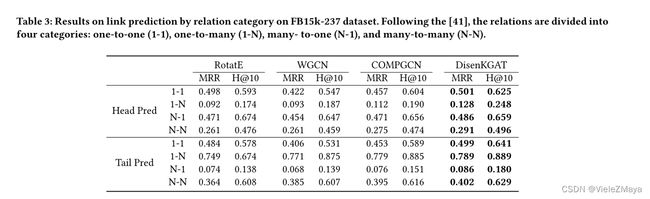
针对复杂的多关系场景,特别是1-N、N-1和N-N关系的问题(如表3所示),作者选择了具有丰富的多关系和密集的图结构的FB15k-237作为研究对象,并将模型与ROTATE , W-GCN, COMPGCN进行比较。
发现DisenKGAT在所有关系类型中都优于Baseline,这表明充分利用图结构有利于处理复杂关系,并且此模型倾向于捕捉复杂场景中丰富的潜在因素,会聚合那些潜在的相似“主题”的邻居,从而在简单关系和复杂关系上都大大优于其他模型。
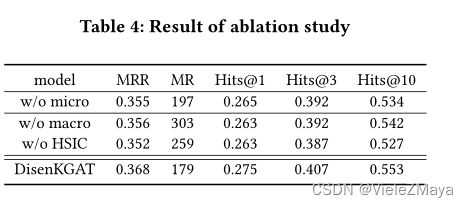
5.2 消融实验(RQ2)
本文对聚集机制、独立建模、注意评分和几个超参数的存在性进行了消融研究。
去除解耦
无微观解耦效果下降显著,主要是缺少多子语义表征嵌入以及动态性聚合帮助其生成包含“簇”(主题)的邻居子集,模型退化为一般的基于 GCN 的图谱补全模型。
无宏观解耦,则无法保证子语义表征的分离与差别化,实验中发现无独立性限制会到导致其自身训练过程中信息再次杂糅耦和,丧失解耦意义。特别的,去除独立性正则方法HISC,很容易导致聚合的信息在给定场景中不具有代表性。
不同子语义数量
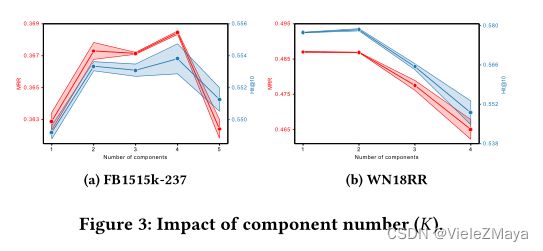
图3总结了FB15k-237和WN18RR数据集的实验结果。为探究不同数据集子语义 K K K值影响,调整 K K K值发现:FB15k-237 由于丰富的语义关系,其呈现先升后降的趋势。当 K K K值过大,我们认为主题数量过多将导致主题划分过于精细化,细粒度过深,无法保证每个隐因子携带其关键信息,并且造成信息融合过拟合了 。WN18RR 由于语义简单,因此 K K K值增大效果持续下降。
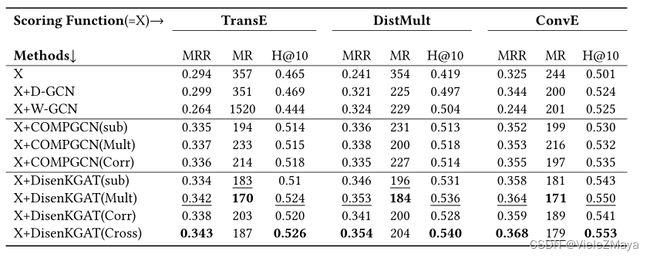
5.3 鲁棒性(RQ3)
DisenKGAT在知识图嵌入方面具有较强的鲁棒性,可以与多类别评分函数协同工作,具有较大的改进。
打分函数方面,采用了三种:TransE(翻译)、DistMult(语义匹配)和ConvE(基于神经的模型)
信息融合函数方面,采用了四种:减法、乘法、交叉作用与循环卷积
注意到:
-
图卷积网络可以进一步挖掘图的结构信息,由于在聚合阶段没有考虑将嵌入到传播层中的关系纳入其中,W-GCN和D-GCN在各种评分函数中表现不佳。
-
与COMPGCN相比,由于关系感知聚合和互信息正则化的设计赋予模型丰富的结构信息和分离的潜在因素,可以在所有指标上大大超过Baseline。
再次注意到,与其他组合不同的是,模型在减法融合函数中加入了TransE评分函数(sub+TransE),结果差强人意。原因是TransE中使用的内在结构的肤浅,这很难捕获实体和关系之间深度复杂的交互。
5.4 案例分析(RQ4)
利用测试集中每个实体已经解耦过的语义空间来研究解耦因素如何促进实体的表征。下图为两个来自FB15k-237的例子直观展示其的解耦性能。
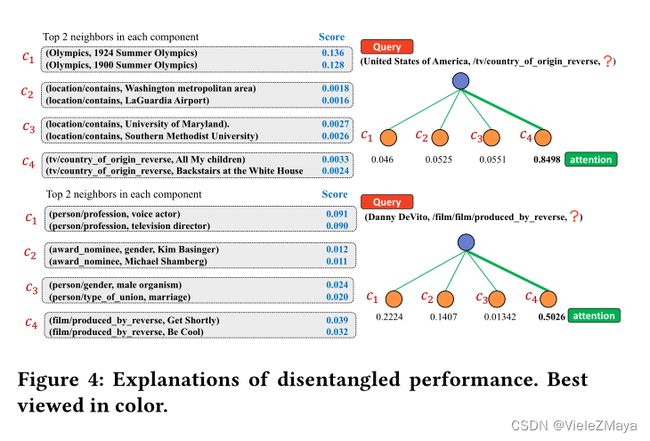
从实验列举的案例(略)中可知,不同实体子语义权重最高的两个邻居信息,实验发现各个语义有较强的主题信息,且不同主题具有显著差异性。同时由于不同语义(通道)信息彼此共享,因此两个相关联实体在部分语义主题一致。
6 CONCLUSION AND FUTURE WORK
本文提出了一种新型的知识图谱解耦表征学习框架DisenKGAT,该模型从微观和宏观两个方面对解耦因素进行了充分利用:
-
利用一种新型的关系感知聚合机制,在保证结构信息的前提下实现微观解耦;
-
考虑了宏观可分离性,采用互信息最小化作为正则化方法。此外,还以各种实验来验证我们的模型的有效性和可解释性。
在未来的工作中,作者将探索一个更通用的解耦框架,它可以适应更复杂的场景。例如,如何在细粒度级别上分离知识图谱,其中每个实体的子表征数量可以是不同且灵活的。此外,作者还计划在更多不同的场景中探索互信息的潜力,而不仅仅是单纯地正则化。
参考:
https://zhuanlan.zhihu.com/p/428860159
https://blog.csdn.net/VieleZMaya/article/details/128043290