《MonoRec：Semi-Supervised Dense Reconstruction in Dynamic Environments from a Single Moving Camera》

参考代码：MonoRec

1. 概述

介绍：这篇提出了一种纯视觉的自监督深度估计算法，它结合现有实例分割、视觉里程计等视觉相关领域中相关技术，构造出这篇提出的MonoRec单目深度估计方法（在做训练的时候也采用了双目的图像作为输入）。在自监督单目深度估计网络中，一个很大的困难便是需要区分哪些像素相对相机参考系是存在运用的，这是文章引入实例分割方法得到的mask去引导并构建MaskModule去解决存在“运动”的目标。对于深度估计部分，这里是使用”运动“目标mask和由输入图片构建的cost volume去预测对应的深度结果，相比MonoDepth系列少了pose预测部分（pose参数是通过加载数据集实现的）。此外，对于上述的mask和depth两个任务训练，文章的方法比较繁琐了（为多阶段训练策略），首先需要分别完成mask和depth的bootstrapping训练，之后再在depth和mask网络预训练基础上对应网络的进一步优化工作。

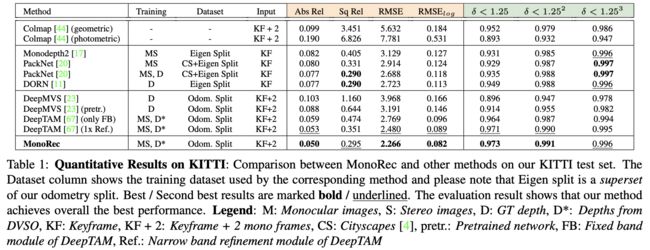
这篇文章主要工作体现在使用一个MaskModule去预测“运动”目标，从而避免这类目标在深度估计结果中存在的”空洞”问题，并使用视觉里程计方法产生的稀疏深度监督点进行深度估计约束，从而构建了一个对摄像头视野中“运动”比较鲁棒的自监督深度估计方法。只不过这里是使用Mask RCNN去完成可能存在“运动”的目标，但是在自然条件下该方法也是有较大限制的，毕竟可运动的物体太多了，而且还在训练的过程中假设了pose是已知的。整体上来讲文章方法在KITTI数据及上深度估计表现的结果还是不错的，如下图所示 ：

2. 方法设计

2.1 整体pipeline

文章的整体pipeline见下图所示：

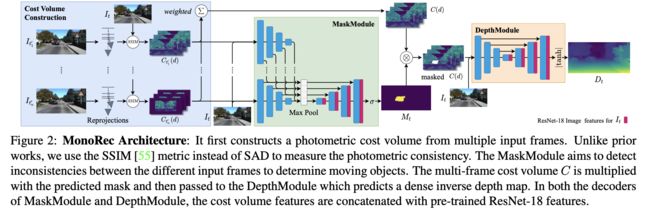
从上图可知输入的视频序列会在先期深度假设条件下生成Cost Volume $C(d)$，之后送入MaskModule得到“运动”物体的mask结果$M_t$，最后结合之前的输出得到最后的深度估计结果$D_t$。对于输入的单目视频序列$\{I_1,\dots ,I_N\}$（一般$N=3$），扣留关键帧$t$之后的额外帧为$I_{t^{{}^{\prime }}}(t^{{}^{\prime }}\in \{1,\dots ,N\}/t)$。则在上述给定深度估计结果和pose参数（$T_{t^{{}^{\prime }}}^t$）的情况下可以实现帧间映射：
$$I_{t^{{}^{\prime }}}^t=I_{t^{{}^{\prime }}}⟨proj(D_t,T_{t^{{}^{\prime }}}^t)⟩$$
此外，在文章算法的训练过程中除了单目的时序序列$T$（temporal frames）之外还是用了双目视觉中的另外一个视角图像$S$（static stereo），从而引入更多信息以帮助生成更好的深度估计结果。

2.2 子模块

2.2.1 Cost Volume构建

在构建Cost Volume过程中是将帧$I_{t^{{}^{\prime }}}$在不同深度参数$d$（该参数通过最小最大深度进行线性划分确定）投影到关键帧$I_t$下构建的，这里对于Cost Volume在不同深度参数下的重构度量表示为：
$$pe(x,d)=\frac{1-SSIM(I_{t^{{}^{\prime }}}(x,d),I_t(x))}{2}$$
其中，$x$是对应的像素表示。那么Cost Volume在该基础上被描述为：
$$C(x,d)=1-\frac{2}{{\sum }_{t^{{}^{\prime }}}{w}_{t^{{}^{\prime }}}}\cdot \sum p{e}_{t^{{}^{\prime }}}^t(x,d)\cdot w_{t^{{}^{\prime }}}(x)$$
注意在上式子中存在一个加权因子$w_{t^{{}^{\prime }}}(x)$，其是通过与最小重构误差的差值建立关系的：
$$w_{t^{{}^{\prime }}}(x)=1-\frac{1}{M-1}\cdot \sum _{d\ne d^{\ast }}exp(-\alpha (p{e}_{t^{{}^{\prime }}}^t(x,d)-p{e}_{t^{{}^{\prime }}}^t(x,d^{\ast }){)}^2)$$
其中，需要求取重构误差最小对应的深度：$d_{t^{{}^{\prime }}}^{\ast }=\underset{d}{\mathrm{argmin}}p{e}_{t^{{}^{\prime }}}^t(x,d)$。对应的实现可以参考代码：

# model/monorec/monorec_model.py#L132
class CostVolumeModule(nn.Module):
    ...

2.2.2 MaskModule

该模块是利用关键帧与其它时序帧$\{I_{t^{{}^{\prime }}}|t^{{}^{\prime }}\in \{1,\dots ,N\}/t\}$构建Cost Volume $\{C_{t^{{}^{\prime }}}|t^{{}^{\prime }}\in \{1,\dots ,N\}/t\}$，之后在此之上使用编解码网络预测得到对应“运动”目标mask。这里将关键帧排除在外，是因为其它帧包含对于“运动”目标的强先验信息。

2.2.2 DepthModule

对于深度估计网络部分这里是采用包含关键帧的所有数据作为输入构建Cost Volume，之后再次基础上预测深度，这样可以使得预测的深度更加准确和鲁棒。

2.3 训练策略

文章的训练策略主体上可以划分为2个步骤：Bootstrapping和Refinement。在前一个步骤中完成mask和depth网络部分的单独训练，后一个步骤中实现mask和depth的交替优化过程。

2.3.1 BootStrapping

depth部分：
在对depth预测结果进行预测的时候文章采取了3个分量的约束：重投影误差约束、视觉里程计稀疏深度约束、深度梯度平滑约束。其中重投影误差约束部分其使用SSIM和L1的形式：
$$L_{self,s}=\underset{t^{\ast }\in t^{{}^{\prime }}\cup \{t^S\}}{\min }(\lambda \frac{1-SSIM(I_{t^{\ast }}^t,I_t)}{2}+(1-\lambda )|I_{t^{\ast }}^t-I_t{|}_1)$$
对于视觉里程计得到的稀疏深度，使用如下方式进行约束：
$$L_{sparse,s}=|D_t-D_{VO}{|}_1$$
因而总的约束被描述为：
$$L_{depth}=\sum _{s=0}^3{L}_{self,s}+\alpha L_{sparse,s}+\beta L_{smooth,s}$$

mask部分：
这里使用Mask RCNN去检测场景中能够运动的目标mask（具有较大限制）之后按照不一致准则确定具体mask，其具体的判断度量依据源自于如下3点（这里令时序图像和双目图像对构建的Cost Volume为$C,C^S$，以及深度估计网络得到的深度结果$D_t,D_t^S$）：

• 1）深度$D_t$与双目图像的重构误差$p{e}_{t^S}^t(x,D_t(x))$；
• 2）时序帧与双目深度组合构建的平均重构误差$\overline{p{e}_{t^{‘}}^t}(x,D_t^S(x))$；
• 3）时序预测深度和双目深度的差异；

下面是经过筛选之后用于训练“运动”掩膜的图像示例：

2.3.2 Refinement

该阶段是间隔使用depth和mask预训练参数实现对应任务的优化。

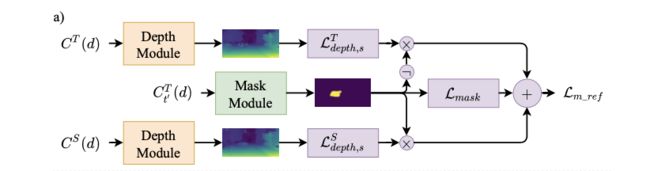
Mask部分：
这部分使用了bootstrapping中得到的预训练参数实现mask部分优化：
$$L_{m\_ref}=\sum _{s=0}^3(M_t{L}_{depth,s}^{{}^{\prime }S}+(1-M_t)L_{depth,s}^{{}^{\prime }T})+L_{mask}$$
其数据流程见下图所示 ：

Depth部分：
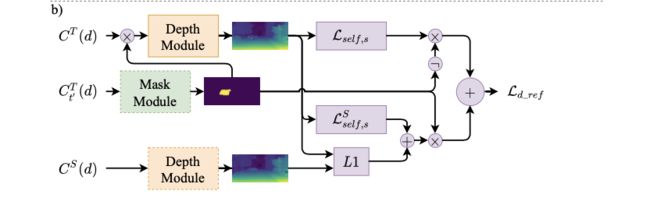
depth部分使用了MaskModule的输出进行depth的优化：
$$L_{d\_ref,s}=(1-M_t)(L_{self,s}+\alpha L_{sparse,s})+M_t(L_{self,s}^S+\gamma |D_t-D_t^S{|}_1)+\beta L_{smooth,s}$$
其数据流程见下图所示 ：

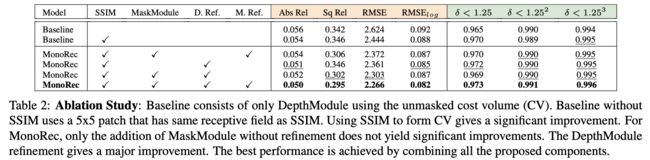
综合上述内容，对其中的一些算法分量进行定量消融实验得到下表结果 ：

3. 实验结果

KITTI数据集上性能对比：