K-Means(K均值聚类)原理及代码实现
机器学习
没有免费午餐定理和三大机器学习任务
如何对模型进行评估
K-Means(K均值聚类)原理及代码实现
KNN(K最近邻算法)原理及代码实现
KMeans和KNN的联合演习
文章目录
- 机器学习
- 前言
- 一、算法步骤
- 二、例子
-
- 1. K=2 选取P3和P4作物簇心
- 2.计算每个点到簇心的距离
- 3. 更新簇心。
- 3. 再次计算每个点到簇心的距离。
- 三、代码实现
-
- 1. 导入必要的库
- 2. K-Means实现
- 3. 绘制分类图(二维情况下)
- 4. 运行代码
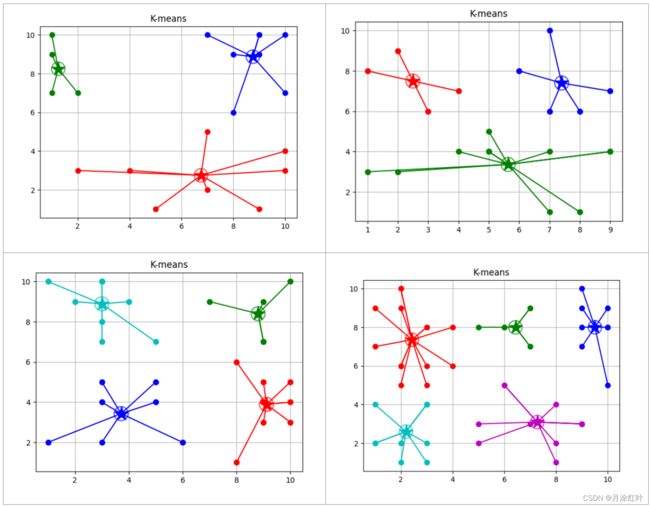
- 四、测试结果
前言
K-Means算法是机器学习中一个非常简单且使用的聚类算法。其只具备一个超参数K,代表着样本的类别数。
假设k=2则表示我们希望将样本分为两类,另外k-means能够自主寻找样本数据的内部结构。
该算法是基于假设:特征空间中相近的两个样本很可能属于同一类别。
因为它所使用的数据不带有标签,所以毫无疑问是一种无监督学习方法。
其具备一下优点
- 可解释性好。
- 实现简单。
- 分类效果不错。
但是也存在一些缺点:
- 准确度不如监督学习。
- 对K值的选择很敏感。
一、算法步骤
- 先定义有多少个簇/类别(cluster),即确定K值。
- 将每个簇心(中心)随机定在样本点上。
- 每个样本关联到最近的簇心上。
- 重新计算每个簇的簇心位置(取每个点坐标的平均值)。
- 更改簇心。
- 不停重复,直到簇心不变。
二、例子
该例子来自于【10分钟算法系列】K均值聚类算法-带例子/K-Means Clustering Algorithm
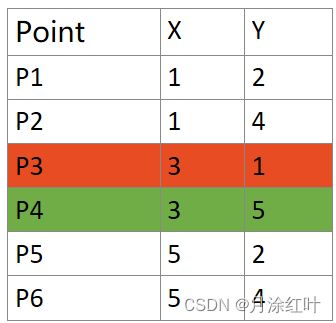
1. K=2 选取P3和P4作物簇心
2.计算每个点到簇心的距离
此处 D ( C n ) 2 D(C_n)^2 D(Cn)2表示样本点到第n个簇心的距离的平方(简化计算)。

其中点 P1, P3, P5是一类, P2, P4, P6是另一类。
3. 更新簇心。
3. 再次计算每个点到簇心的距离。

所有样本所属的簇没有改变,所有簇心不变,循环结束,分类完成。
三、代码实现
1. 导入必要的库
import random
import sys
import numpy as np
import matplotlib.pyplot as plt
2. K-Means实现
class KMeans(object):
def __init__(self, input_data, k):
# data是一个包含所有样本的numpy数组
# data示例,每行是一个坐标
# [[1 2],
# [2 3],
# [3 4]]
self.data = input_data
self.k = k
# 保存聚类中心的索引和类样本的索引
self.centers = []
self.clusters = []
self.capacity = len(input_data)
self.__pick_start_point()
def __pick_start_point(self):
# 随机确定初始簇心
self.centers = []
if self.k < 1 or self.k > self.capacity:
raise Exception("K值错误")
indexes = random.sample(np.arange(0, self.capacity, step=1).tolist(), self.k)
for index in indexes:
self.centers.append(self.data[index])
def __distance(self, i, center):
diff = self.data[i] - center
return np.sum(np.power(diff, 2))**0.5
def __calCenter(self, cluster):
# 计算该簇的中心
cluster = np.array(cluster)
if cluster.shape[0] == 0:
return False
return (cluster.T @ np.ones(cluster.shape[0])) / cluster.shape[0]
def cluster(self):
changed = True
while changed:
self.clusters = []
for i in range(self.k):
self.clusters.append([])
for i in range(self.capacity):
min_distance = sys.maxsize
center = -1
# 寻找簇
for j in range(self.k):
distance = self.__distance(i, self.centers[j])
if min_distance > distance:
min_distance = distance
center = j
# 加入簇
self.clusters[center].append(self.data[i])
newCenters = []
for cluster in self.clusters:
newCenters.append(self.__calCenter(cluster).tolist())
if (np.array(newCenters) == self.centers).all():
changed = False
else:
self.centers = np.array(newCenters)
3. 绘制分类图(二维情况下)
def plotKmeans(cluster):
xdata = []
ydata = []
for Cluster in cluster.clusters:
xsubdata = []
ysubdata = []
for point in Cluster:
xsubdata.append(point[0])
ysubdata.append(point[1])
xdata.append(xsubdata)
ydata.append(ysubdata)
colors = ['r', 'g', 'b', 'c', 'm', 'y', 'k']
for i in range(len(xdata)):
for j in range(len(xdata[i])):
x = np.array([xdata[i][j], cluster.centers[i][0]])
y = np.array([ydata[i][j], cluster.centers[i][1]])
plt.plot(x, y,
color=colors[i], # 全部点设置为红色
marker='o', # 点的形状为圆点
ms=7,
linestyle='-')
plt.plot([cluster.centers[i][0]], [cluster.centers[i][1]],
color=colors[i], # 全部点设置为红色
marker='*', ms=20, # 点的形状为圆点
linestyle='-')
plt.scatter(cluster.centers[i][0], cluster.centers[i][1], s=350, c='none',
alpha=0.7, linewidth=1.5, edgecolor=colors[i])
plt.grid(True)
plt.title("K-means")
plt.show()
4. 运行代码
from KMeans import KMeans, plotKmeans
import random
import numpy as np
if __name__ == '__main__':
points = []
data = []
i = 0
while i < 20:
point = [random.randint(1, 10), random.randint(1, 10)]
# 去掉重复点,否则会导致错误
if point not in points:
points.append(point)
data.append(np.array(point, dtype='float64'))
i += 1
cluster = KMeans(data, 3)
cluster.cluster()
plotKmeans(cluster)