R语言在散点图中添加lm线性回归公式
R语言在散点图中添加lm线性回归公式
-
-
-
- 1. 简单的线性回归
- 2. 使用ggplot2展示
- 3. 提取线性回归p值
-
-
1. 简单的线性回归
函数自带的例子(R 中键入?lm),lm(y ~ x)回归y=kx + b, lm( y ~ x -1 )省略b,不对截距进行估计:
require(graphics)
## Annette Dobson (1990) "An Introduction to Generalized Linear Models".
## Page 9: Plant Weight Data.
ctl <- c(4.17,5.58,5.18,6.11,4.50,4.61,5.17,4.53,5.33,5.14)
trt <- c(4.81,4.17,4.41,3.59,5.87,3.83,6.03,4.89,4.32,4.69)
group <- gl(2, 10, 20, labels = c("Ctl","Trt"))
weight <- c(ctl, trt)
lm.D9 <- lm(weight ~ group)
lm.D90 <- lm(weight ~ group - 1) # omitting intercept
anova(lm.D9)
summary(lm.D90)
opar <- par(mfrow = c(2,2), oma = c(0, 0, 1.1, 0))
plot(lm.D9, las = 1) # Residuals, Fitted, ...
par(opar)
使用R中自带的mtcars数据,可以得到截距和斜率,也可以得到解释率R-square:
require(ggplot2)
library(dplyr) #加载dplyr包
library(ggpmisc) #加载ggpmisc包
library(ggpubr)
require(gridExtra)
model=lm(mtcars$wt ~ mtcars$mpg)
model
## 输出:
Call:
lm(formula = mtcars$wt ~ mtcars$mpg)
Coefficients:
(Intercept) mtcars$mpg
6.047 -0.141
```
```handlebars
summary(model)
## 输出:
Call:
lm(formula = mtcars$wt ~ mtcars$mpg)
Residuals:
Min 1Q Median 3Q Max
-0.652 -0.349 -0.138 0.319 1.368
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6.0473 0.3087 19.59 < 2e-16 ***
mtcars$mpg -0.1409 0.0147 -9.56 1.3e-10 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.494 on 30 degrees of freedom
Multiple R-squared: 0.753, Adjusted R-squared: 0.745
F-statistic: 91.4 on 1 and 30 DF, p-value: 1.29e-10
提取回归R-square值:
通过summary提取:
## 上面的例子
## mtcars例子
model=lm(mtcars$wt ~ mtcars$mpg)
res=summary(model)
str(res)
## 提取各个值:
res$r.squared
res$coefficients
res$adj.r.squared ## df 矫正后的结果
res$coefficients[1,1]
res$coefficients[2,1]
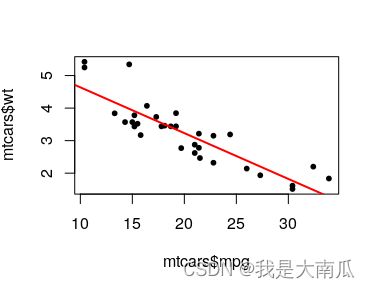
使用默认的plot绘制回归散点:
plot(mtcars$mpg, mtcars$wt, pch=20,cex=2)
abline(model,col="red",lwd=2)
test=mtcars[c("mpg","wt")]
head(test)
colnames(test)=c("x","y")
model = lm(y ~ x, test)
test$predicted = predict(
object = model,
newdata = test)
test$CI = predict(
object = model,
newdata = test,
se.fit = TRUE
)$se.fit * qt(1 - (1-0.95)/2, nrow(test))
test$predicted = predict(
object = model,
newdata = test)
test$CI_u=test$predicted+test$CI
test$CI_l=test$predicted-test$CI
plot(mtcars$mpg, mtcars$wt, pch=20,cex=1) ## have replicated x values
abline(model,col="red",lwd=2)
lines(x=test$x,y=test$CI_u,col="blue")
lines(x=test$x,y=test$CI_l,col="blue")
plot(mtcars$mpg, mtcars$wt, pch=20,cex=1,type="b") ## have replicated x values

实际上面的计算方法没问题,但是数据不合适,因为数据x含有重复值,所以要考虑这个。
2. 使用ggplot2展示
ggplot2例子:
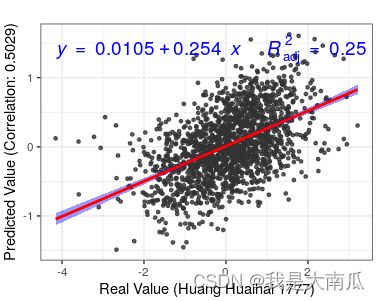
p <- ggplot(df, aes(x=yreal, y=ypred)) +
geom_point(color = "grey20",size = 1, alpha = 0.8)
#回归线
#添加回归曲线
p2 <- p + geom_smooth(formula = y ~ x, color = "red",
fill = "blue", method = "lm",se = T, level=0.95) +
theme_bw() +
stat_poly_eq(
aes(label = paste(..eq.label.., ..adj.rr.label.., sep = '~~~')),
formula = y ~ x, parse = TRUE,color="blue",
size = 5, #公式字体大小
label.x = 0.05, #位置 ,0-1之间的比例
label.y = 0.95) +
labs(title="test",x="Real Value (Huang Huaihai 1777)" , y="Predicted Value (Correlation: 0.5029)")
p2
ggplot版本的手动计算:
require(ggplot2)
library(dplyr) #加载dplyr包
library(ggpmisc) #加载ggpmisc包
library(ggpubr)
require(gridExtra)
ggplot(data=df, aes(x=yreal, y=ypred)) +
geom_smooth(formula = y ~ x, color = "blue",
fill = "grey10", method = "lm") +
geom_point() +
stat_regline_equation(label.x=0.1, label.y=-1.5) +
stat_cor(aes(label=..rr.label..), label.x=0.1, label.y=-2)
test=df
head(test)
colnames(test)=c("x","y")
model = lm(y ~ x, test)
test$predicted = predict(
object = model,
newdata = test)
test$CI = predict(
object = model,
newdata = test,
se.fit = TRUE
)$se.fit * qt(1 - (1-0.95)/2, nrow(test))
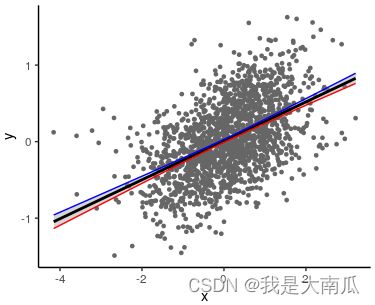
ggplot(test) +
aes(x = x, y = y) +
geom_point(size = 1,colour="grey40") +
geom_smooth(formula =y ~ x,method = "lm", fullrange = TRUE, color = "black") +
geom_line(aes(y = predicted + CI), color = "blue") + # upper
geom_line(aes(y = predicted - CI), color = "red") + # lower
theme_classic()
3. 提取线性回归p值
函数提取 pvalue
fit=lm(df$ypred ~ df$yreal)
fitted=summary(fit)
## get p
lmp <- function (modelobject) {
if (class(modelobject) != "lm") stop("Not an object of class 'lm' ")
f <- summary(modelobject)$fstatistic
p <- pf(f[1],f[2],f[3],lower.tail=F)
attributes(p) <- NULL
return(p)
}
pval=lmp(fit)
一元和多元线性提取一样:
## multiple regression (多元回归)
td=mtcars[c("mpg","wt","drat","disp")]
t=lm(td$wt ~ td$mpg + td$drat + td$disp)
mod_summary=summary(t)
mod_summary$fstatistic
mod_summary$coefficients
##
pf(mod_summary$fstatistic[1], # Applying pf() function
mod_summary$fstatistic[2],
mod_summary$fstatistic[3],
lower.tail = FALSE)
# value
# 2.718e-11
# simple regression(一元回归)
t2=lm(td$wt ~ td$mpg)
mod2_summary=summary(t2)
mod2_summary
pf(mod2_summary$fstatistic[1], # Applying pf() function
mod2_summary$fstatistic[2],
mod2_summary$fstatistic[3],
lower.tail = FALSE)
参考:
https://stackoverflow.com/questions/23519224/extract-r-square-value-with-r-in-linear-models (提取R2)
https://blog.csdn.net/LeaningR/article/details/118971000 (提取R2等)
https://stackoverflow.com/questions/45742987/how-is-level-used-to-generate-the-confidence-interval-in-geom-smooth (添加lm线)
https://zhuanlan.zhihu.com/p/131604431 (知乎)
https://statisticsglobe.com/extract-standard-error-t-and-p-value-from-regression-in-r (提取p值)