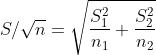R语言数据分析笔记——t检验（含正态性检验和方差齐性检验在SPSS和R语言中的操作&t检验（单样本、双独立样本、配对样本）在Excel、SPSS、R语言中的操作）

前言：本文为个人学习笔记，为各大网站上的教学内容之综合整理，综合整理了①假设分析的基础知识、②正态性检验和方差齐性检验在SPSS和R语言中的操作、③t检验（单样本、双独立样本、配对样本）在Excel、SPSS、R语言中的操作，尽量标明出处。另因能力所限或有纰漏之处，故仅供参考，欢迎交流指正。

基础知识

推荐资料：

B站张文彤  统计分析轻松入门  推荐观看P32~P38

7.1为什么要学习假设检验？_哔哩哔哩_bilibili7.1为什么要学习假设检验？是统计分析轻松入门的第32集视频，该合集共计41集，视频收藏或关注UP主，及时了解更多相关视频内容。https://www.bilibili.com/video/BV1h541147xB?p=32&vd_source=e7e2a58a4620baadd97797801e55b129https://www.bilibili.com/video/BV1h541147xB?p=32&vd_source=e7e2a58a4620baadd97797801e55b129

B站陈祥雨大猫咪老师

PPT 通俗统计学原理入门14 单样本t检验 - 哔哩哔哩大家好。到目前为止，我们已经学习了足够多的统计学基础概念。本节课，我们通过统计学软件中的实际操作，来学习一下单样本t检验的概念和方法，并以此来加深对已经学过的概念的理解。假如是通过关键词搜到本节课的同学，建议从本课程系列的第一节课开始看起。本节课不再对各个概念做过多的解释。我们仍然以英语成绩为例。例如，有一个高中，王老师负责一个高三班级的英语课程，班级内有20位同学。在某次全年级英语考试后，全校的英语平均分为137分，王老师班的平均分为135.8分。https://www.bilibili.com/read/cv16868297?spm_id_from=333.999.0.0https://www.bilibili.com/read/cv16868297?spm_id_from=333.999.0.0PPT 通俗统计学原理入门17 样本独立性 独立样本 配对t检验 - 哔哩哔哩大家好，上一节课中，我们学习了“双样本t检验”和“独立样本t检验”是一回事。独立，independent，不是“单独”，single。所以，独立样本t检验，是两个样本之间的t检验，不能多，也不能少，就是两个。这节课，我们来通俗讲解一下样本之间“相互独立”的含义。我们仍然回到上节课的故事中。一个县城，有两个中学，一中和二中，每个中学都有1000个学生。县教育局想比较一下两个中学的总体英语水平，于是组织了一次统考，一中和二中考同一份试卷。考完之后，由于时间仓促，两个学校各自的总体均分μ1和μ2，还没https://www.bilibili.com/read/cv16969556?spm_id_from=333.999.0.0https://www.bilibili.com/read/cv16969556?spm_id_from=333.999.0.0假设检验可以解决什么问题？

参数估计：从样本到总体

假设检验的意义：对提出的总体假设进行分析判断，以做出决策

如何利用假设检验解决问题？

运用统计知识根据研究设计和资料性质选择正确的分析过程

初步的统计描述：集中趋势、离散趋势、分布特征、异常值及其他

假设检验原理

现有的样本均数和已知总体均数不同，差别可能来源于两个方面：

1.样本来自已知总体，现有差别为抽样误差

2.样本来自其他总体（与已知总体不同），存在本质差异

所有需要用统计学方法判断误差来源，即进行假设检验

假设检验前提

小概率原理：认为小概率事件在一次随机抽样中不会发生

（事实上小概率事件在随机抽样中可能发生，但是概率很小，若正好碰上，则假设检验的结论是错误的。但这种错误是我们为了做出统计决策愿意付出的代价。）

假设检验步骤

1.建立假设

检验假设，记为：

备择假设，记为：

2.确定检验水准

检验水准，指本来成立，却根据样本信息拒绝的可能性大小。即拒绝时最大允许误差的概率，常用0.05。

3.计算统计量和P值

检验统计量的特点

该统计量应当服从某种已知分布（t分布、分布、F分布等等），从而可以计算出P值。

P值

P值，从假设的总体中抽出现有样本（及更极端情况）的概率。 

P值可以客观衡量样本对假设总体偏离程度。

4.得出结论

按照事先确定的界定P值对进行取舍，作出推断结论，引申出实用性结论。  

若P≤

认为出现了小概率事件，拒绝接受。可以认为样本与总体的差异存在本质区别，而非偶然，这种差别有统计学意义。

若P> 

认为出现了常见事件，不拒绝。可以认为样本与总体的差异不存在本质区别，可能存在偶然，两者差别无统计学意义。

Ⅰ型错误和Ⅱ型错误

	拒绝，接受	不拒绝
真实	Ⅰ型错误（）	正确推断（1-）
不真实	正确推断（1-）	Ⅱ型错误（）

检验效能：是真的，实际拒绝的概率=1-

实际问题中往往希望得到拒绝的结论，所以检验效能不应当太低

如何控制两种错误

可以事先认为设定

只能间接控制

1.增大样本量以减小标准误（标准误减小1倍，样本量需增大4倍）

2.放大来减小

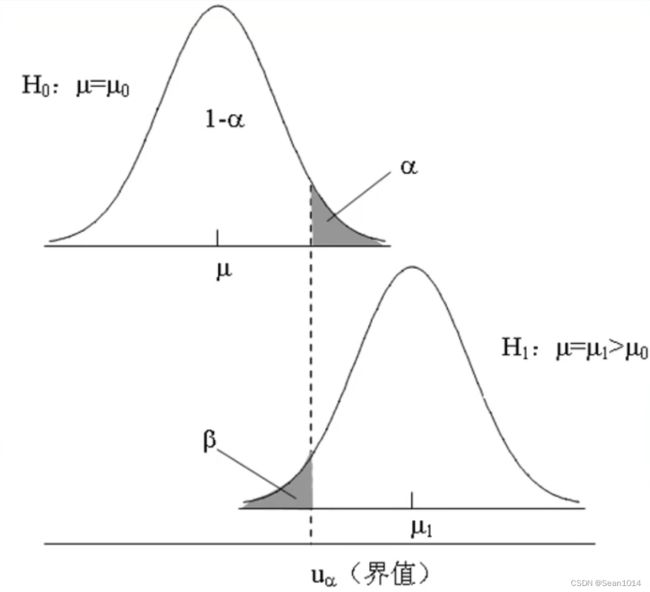Ⅰ型错误和Ⅱ型错误示意图（以单侧t检验为例）

假设检验的结论不能绝对化

保留了犯错误的可能性

样本量导致检验效能问题

1.样本量太小，导致检验效能不足，无法检出可能存在的差异

2.样本量太大，得出有统计学意义的结论，但是这种结论可能没有实际意义

假设检验的单侧和双侧问题

双侧检验：不知道样本所在总体与假定总体的大小关系。得到拒绝结论更困难，结果更稳妥。

单侧检验：根据专业知识确定样本所在总体与假定总体的大小关系。敏感，得到拒绝结论更容易。

统计方法适用条件

独立性：绝大部分方法都要求

正态性：t检验、方差分析常见要求

方差齐性：t检验、方差分析常见要求

正态性和方差齐性检验

正态性检验

SPSS

SPSS第三讲 | 正态分布怎么检验？看这篇文章就够了 - 知乎

SPSS非参数两独立样本检验 - 知乎

方法1：画图法

直方图：【操作】图形-旧对话框-直方图，选择变量，勾选显示正态曲线，确定。观察直方图的分布形状是否为一个倒扣“钟”型的对称形状，如果接近或相似，则可认为数据服从正态分布。

正态Q-Q图：【操作】分析-描述统计-Q-Q图，选择变量，检验分布选择正态，确定。若数据服从正态分布，则数据点应与理论直线基本重合。

正态P-P图：【操作】【操作】分析-描述统计-P-P图，选择变量，检验分布选择正态，确定。若数据服从正态分布，则数据点应与理论直线基本重合。

方法2：计算偏度和峰度

当偏度S≈0时，可认为分布是对称的，服从正态分布（不左不右）；当峰度K≈0时，可认为分布的峰态合适，服从正态分布（不胖不瘦）。

SS和SK均为S系数和K系数的标准误。在=0.05的情况下，若Z的绝对值大于1.96，可认为K系数或S系数显著不等于0，即样本数据非正态。 若Z的绝对值小于1.96，可认为样本数据满足正态分布。

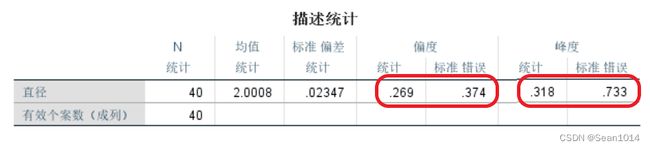
【操作】分析-描述统计-描述，选择变量，选项-勾选平均值、标准偏差、峰度、偏度，继续，确定。

观察描述统计表，

计算偏度系数

计算峰度系数

说明该组样本数据符合正态分布。

方法3：非参数检验法

SPSS

常见的正态性检验有柯尔莫戈洛夫-斯米诺夫检验（K-S检验，适用于大样本数据）和夏皮洛-威尔克检验（S-W检验，适用于小样本数据），当检验结果的P值小于0.05，则认为数据不满足正态性。

例1：当样本量小于50时，采用S-W检验。

【操作】分析-描述统计-探索，因变量和因子列表，图-含检验的正态图，继续，确定。

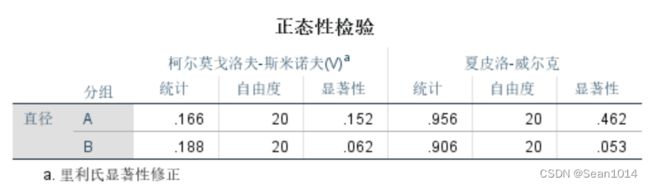
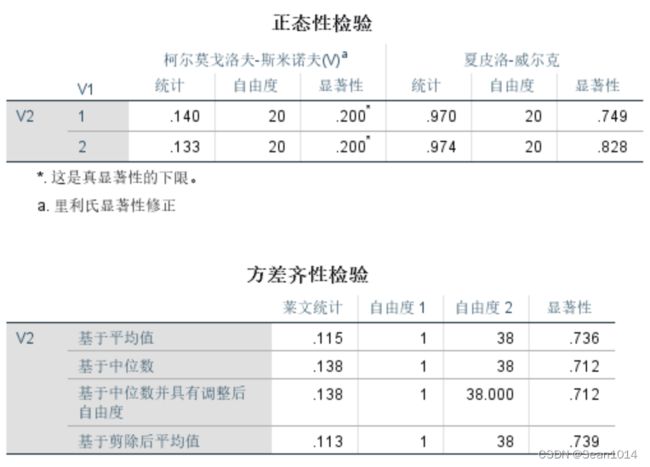
观察正态性检验表，

本例1中，比较A、B两厂所产零件的直径差异，两组样本量均小于50，以S-E检验结果为准，0.462>0.05，0.053>0.05，故认为满足正态性。

例2：当样本量大于等于50时，采用K-S检验。

【操作】分析-描述统计-探索，因变量和因子列表，图-含检验的正态图，继续，确定。

 

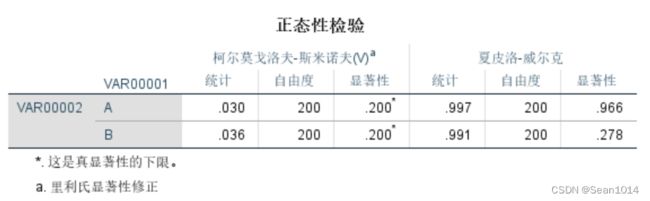
本例2中，比较两组数据差异，两组样本量均大于等于50，以K-S检验结果为准，0.200>0.05，故认为满足正态性。

这个*表示真显著性的下限，具体什么意思我也不太明白，但是>0.05就可以认为满足正态性。

R语言

参考资料：

R语言连续变量正态性检验_奋起的小鹰的博客-CSDN博客_r语言正态性检验

例1：当样本量小于50时，采用S-W检验。

A<-c(1.95,2.01,2.02,1.98,1.97,1.99,2,2.01,2.03,1.98,1.99,1.99,2.01,1.95,1.99,1.98,1.99,2.05,2,1.99)
B<-c(2.03,1.98,1.99,2.05,2.01,2,1.99,1.99,2,2.01,2.03,2.02,1.99,2.05,2,1.99,2,2.01,2.03,1.98)
shapiro.test(A)
shapiro.test(B)

结果如下：

例1结果

对比SPSS的方法结果一致。0.4616>0.05，0.05318>0.05，故认为满足正态性。

例2： 当样本量大于等于50时，采用K-S检验。

C<-c(-1.28,1.57,-0.12,0.22,-0.3,-0.43,-1.17,-0.56,-0.35,-0.04,-0.2,-0.81,-1.81,0.08,1.8,0.96,-0.2,-0.03,-1.7,1.07,-0.73,-0.44,1.35,-0.12,0.55,0.21,0.53,0.25,-0.8,0.63,0.76,-0.79,0.02,-0.13,0.71,-1.04,-0.32,1.32,-1.62,0.75,-0.07,-0.55,-1.23,-0.6,-1.34,0.51,-0.66,-0.45,0.64,-0.08)
D<-c(0.62,0.13,-0.15,0.45,1.72,0.31,-0.93,-1.39,0.05,0.41,0.24,-1.21,2.04,-0.32,1.34,0.06,-0.31,-0.81,0.27,-2.39,0.41,0.57,-0.43,-0.93,1.21,0.14,-1.29,0.07,-0.19,0.08,-0.69,-0.76,0.71,0.84,-1.88,1.43,-1.27,0.39,-0.6,-0.04,-0.22,-1.53,1.73,0.83,-1.57,-0.27,-0.92,0.05,0.45,-0.37)
> ks.test(C,D)

例2结果

对比SPSS的方法P值有微小差别，但结论是一致的，具体原因不明。P值0.5324>0.05，故认为满足正态性。

方差齐性检验

例3：工厂A和工厂B各自生产了一批零件，A工厂抽样20个零件的直径分别为1.95, 2.01, 2.02, 1.98, 1.97, 1.99, 2.00, 2.01, 2.03, 1.98, 1.99, 1.99, 2.01, 1.95, 1.99, 1.98, 1.99, 2.05, 2.00, 1.99，B工厂抽样20个零件的直径分别为2.03, 1.98, 1.99, 2.05, 2.01, 2, 1.99, 1.99, 2, 2.01, 2.03, 2.02, 1.99, 2.05, 2, 1.99, 2, 2.01, 2.03, 1.98，试检验两家工厂的零件是否存在显著差异。

SPSS

SPSS入门教程——方差齐性检验的方法有哪些_nekonekoboom的博客-CSDN博客_方差齐性检验​​​​​​

方法1：Levene（莱文）检验

【操作】分析-描述统计-探索，因变量和因子列表，图-含莱文检验的分布-水平图-未转换，继续，确定。

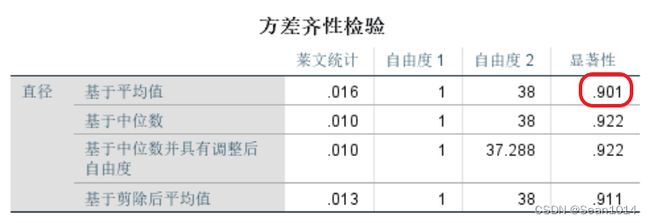
观察方差齐性检验表，

P值0.901>0.05，不拒绝原假设，可认为数据符合方差齐性。

方法2：单因素ANOVA检验

【操作】分析-比较平均值-单因素ANOVA检验，因变量和因子列表，选项-方差齐性检验，继续，确定。

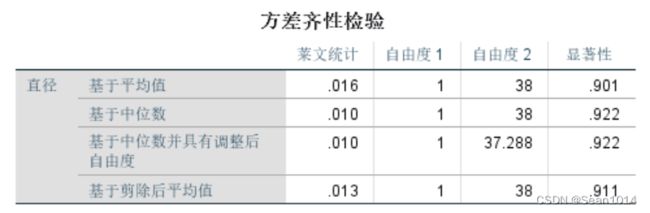与方法1结果相同

P值0.901>0.05，不拒绝原假设，可认为数据符合方差齐性。

R语言

调用car包里的leveneTest函数，第一个参数为数据，第二个参数为分组。

install.packages("car")
library(car)
A<-c(1.95,2.01,2.02,1.98,1.97,1.99,2,2.01,2.03,1.98,1.99,1.99,2.01,1.95,1.99,1.98,1.99,2.05,2,1.99,2.03,1.98,1.99,2.05,2.01,2,1.99,1.99,2,2.01,2.03,2.02,1.99,2.05,2,1.99,2,2.01,2.03,1.98)
B<-rep(c(1,2),each=20)
leveneTest(A,B)

例3结果

这里center=median意思是基于中位数，算出P值为0.9224>0.05（与SPSS结果一样），不拒绝原假设，可认为数据符合方差齐性。

单样本T检验（上机操作）

例1：

工厂生产了一批零件，零件设计的标准直径为2mm，现抽样其中20个零件的直径分别为1.95, 2.01, 2.02, 1.98, 1.97, 1.99, 2.00, 2.01, 2.03, 1.98, 1.99, 1.99, 2.01, 1.95, 1.99, 1.98, 1.99, 2.05, 2.00, 1.99，试检验所得样本的平均数与总体平均数2mm是否存在显著差异。

以下操作省略了检验正态性的步骤。

Excel操作

将数据录入B2~B21列

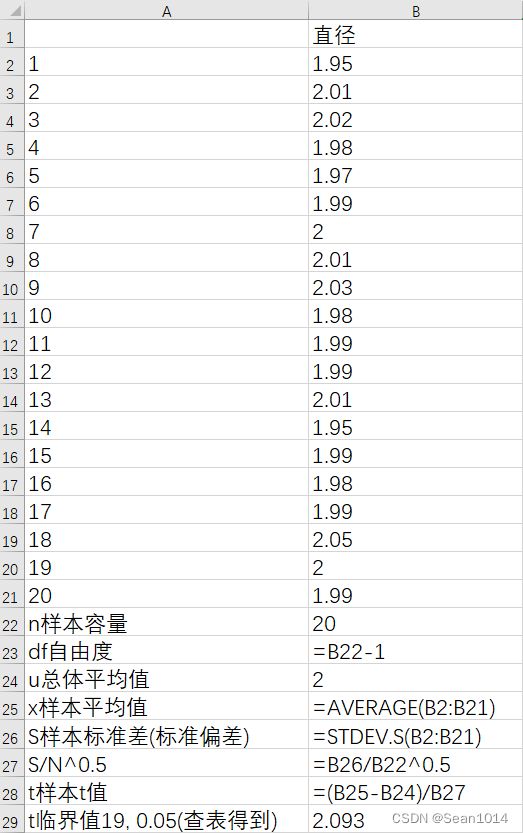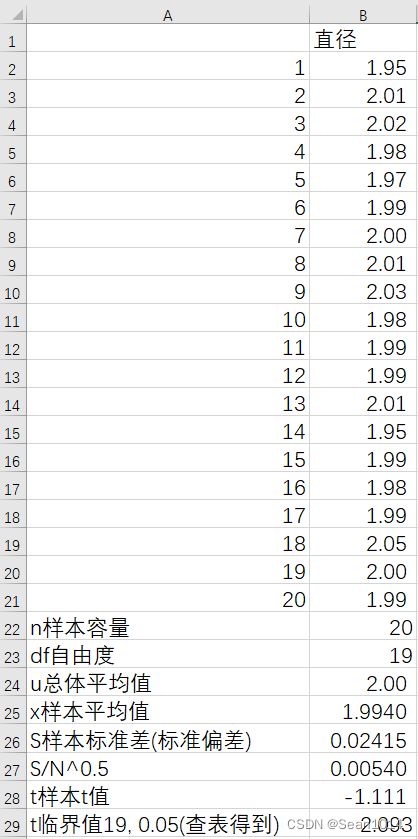显示公式 显示结果

因为是双尾检验，t值绝对值1.111<2.093，说明t值落在了95%置信区间以内。可以认为样本与总体不存在显著差异。 

SPSS操作

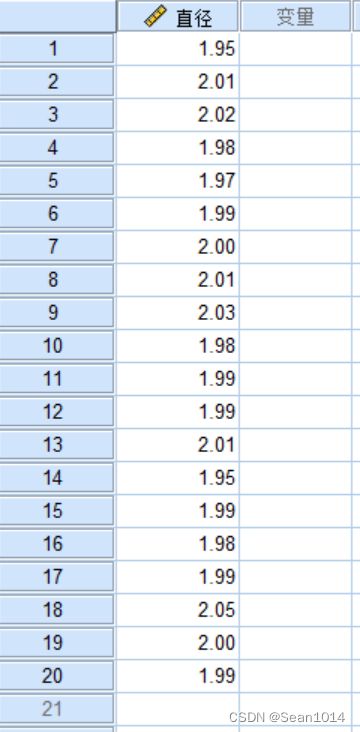录入数据 分析-比较平均值-单样本T检验

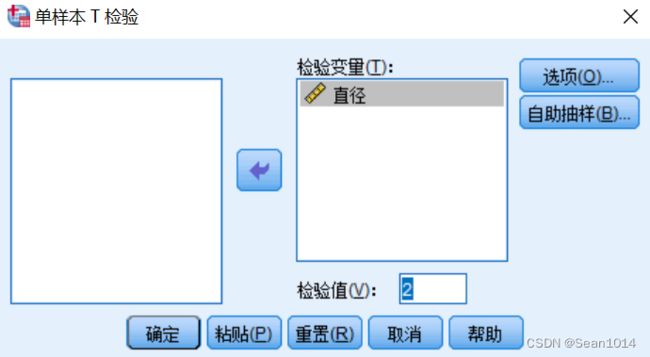检验变量为直径，检验值2 选项-置信区间95%

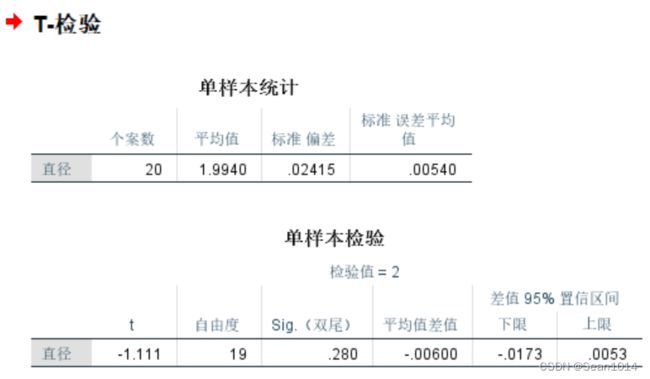对比Excel方法，过程量求出的值一样

这里看Sig.(双尾)，P值0.280>0.05，说明P值落在了95%置信区间以内。可以认为样本与总体不存在显著差异。

R语言操作

注意此处文件名是data1，Sheet1，文件位置在D:/D-WORK/R语言练习/data1.xlsx

library(readxl)
data1<-read_excel('D:/D-WORK/R语言练习/data1.xlsx')
t.test(data1,mu=2,alternative = "two.sided")
#  括号里分别是储存数据的名称、检验值、单尾双尾的参数可选“two.sided”, “less”, “greater”

结果如下：

有3种判断结果的方法

1. 看t值，t=-1.1112，查表可知t临界值19, 0.05为2.093，判断样本与总体不存在显著差异。

2. 看P值，p-value = 0.2804>0.05，判断样本与总体不存在显著差异。

3. 看样本平均值是否落在置信区间以内，1.982698<1.994<2.005302，在区间内，判断样本与总体不存在显著差异。

独立样本T检验（上机操作）

推荐资料：

知乎丁小点

5个步骤，掌握两独立样本T检验 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/104267602

例3：工厂A和工厂B各自生产了一批零件，A工厂抽样20个零件的直径分别为1.95, 2.01, 2.02, 1.98, 1.97, 1.99, 2.00, 2.01, 2.03, 1.98, 1.99, 1.99, 2.01, 1.95, 1.99, 1.98, 1.99, 2.05, 2.00, 1.99，B工厂抽样20个零件的直径分别为2.03, 1.98, 1.99, 2.05, 2.01, 2, 1.99, 1.99, 2, 2.01, 2.03, 2.02, 1.99, 2.05, 2, 1.99, 2, 2.01, 2.03, 1.98，试检验两家工厂的零件是否存在显著差异。

Excel操作

方法1：原始计算法

将数据录入E2~F21列

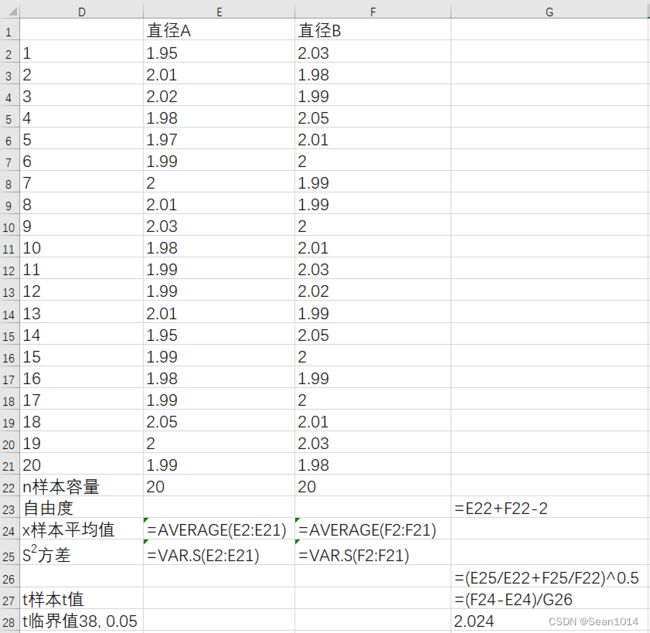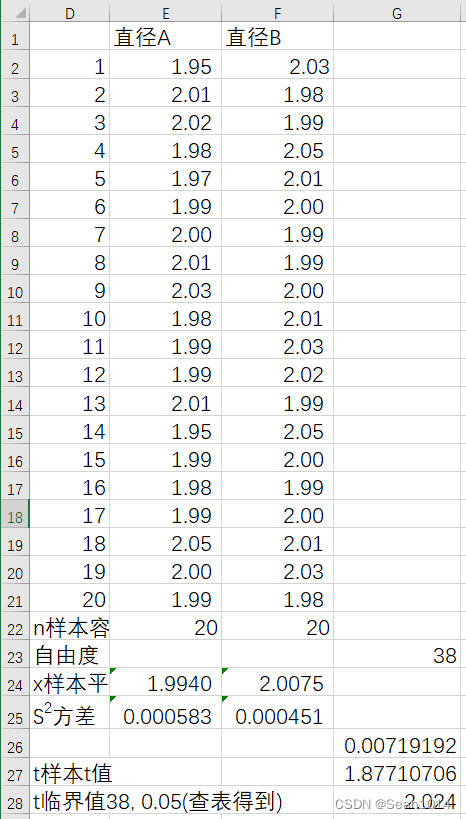显示公式 显示结果

因为是双尾检验，t值绝对值1.877<2.024，说明t值落在了95%置信区间以内。可以认为样本与总体不存在显著差异。 

方法2：数据分析法

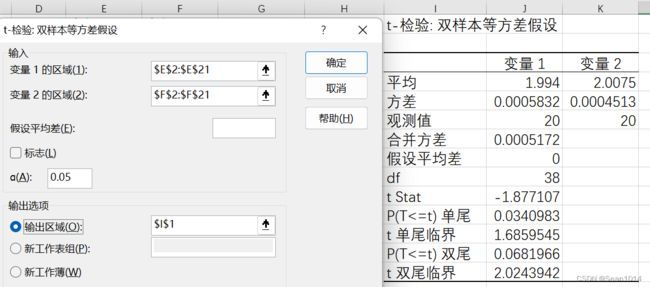
【操作】数据-数据分析（需要在加载项里打开“分析工具库”）-t-检验：双样本等方差假设

选择输入变量的区域，选择输出区域

对比方法1和方法2，过程量求出的值一样。

因为是双尾检验，t值绝对值1.877<2.024，说明t值落在了95%置信区间以内。可以认为样本与总体不存在显著差异。 

SPSS操作

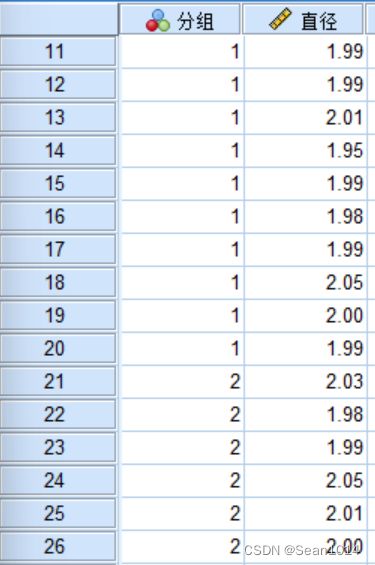分组录入数据 分析-比较平均值-独立样本T检验

定义组 设置

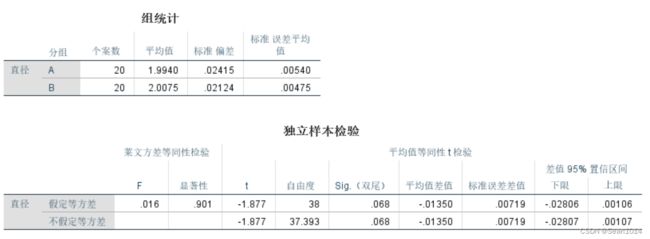结果

这里看Sig.(双尾)，P值0.068>0.05，说明P值落在了95%置信区间以内。可以认为样本与总体不存在显著差异。

R语言操作

A<-c(1.95,2.01,2.02,1.98,1.97,1.99,2,2.01,2.03,1.98,1.99,1.99,2.01,1.95,1.99,1.98,1.99,2.05,2,1.99)
B<-c(2.03,1.98,1.99,2.05,2.01,2,1.99,1.99,2,2.01,2.03,2.02,1.99,2.05,2,1.99,2,2.01,2.03,1.98)
t.test(A,B,alternative= "two.sided")
#  括号里分别是样本1、样本2、单尾双尾的参数可选“two.sided”, “less”, “greater”

结果如下：

有3种判断结果的方法

1. 看t值，t=-1.8771，查表可知t临界值38, 0.05为2.024，判断样本与总体不存在显著差异。

2. 看P值，p-value = 0.06832>0.05，判断样本与总体不存在显著差异。

3. 看平均值之差x-y是否落在置信区间以内，-0.028067047<-0.0135<0.001067047，在区间内，判断样本与总体不存在显著差异。

配对样本T检验（上机操作）

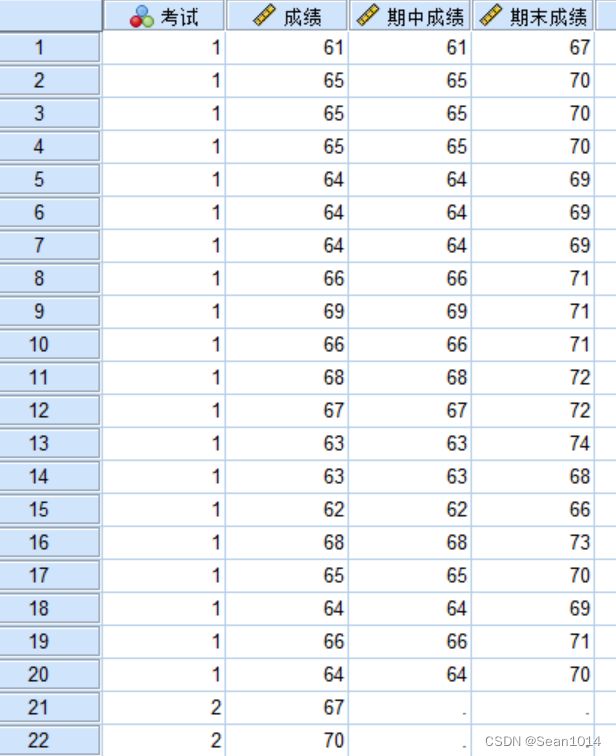
例4：班上有20名同学，期中和期末考试成绩依次分别是65, 65, 65, 65, 64, 64, 64, 66, 66, 66, 67, 67, 63, 63, 62, 68, 65, 64, 66, 65和70, 70, 70, 70, 69, 69, 69, 71, 71, 71, 72, 72, 68, 68, 67, 73, 70, 69, 71, 70。试比较两次考试成绩是否有显著变化？

Excel

将数据录入E2~F21列

方法1：原始计算法

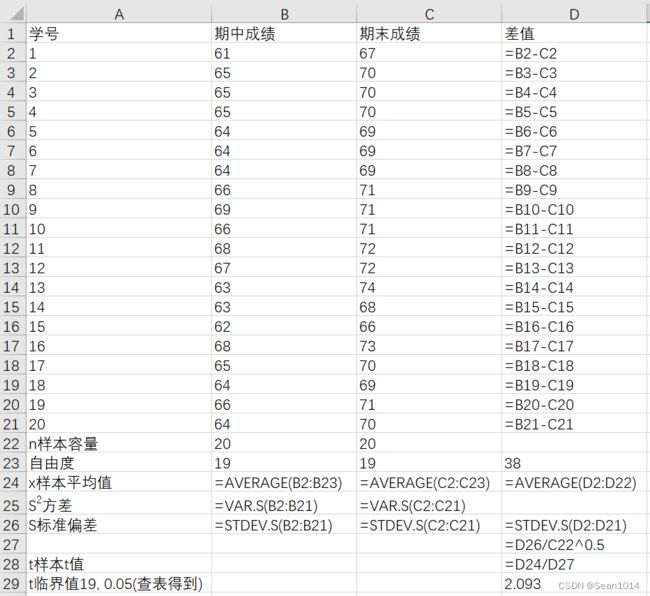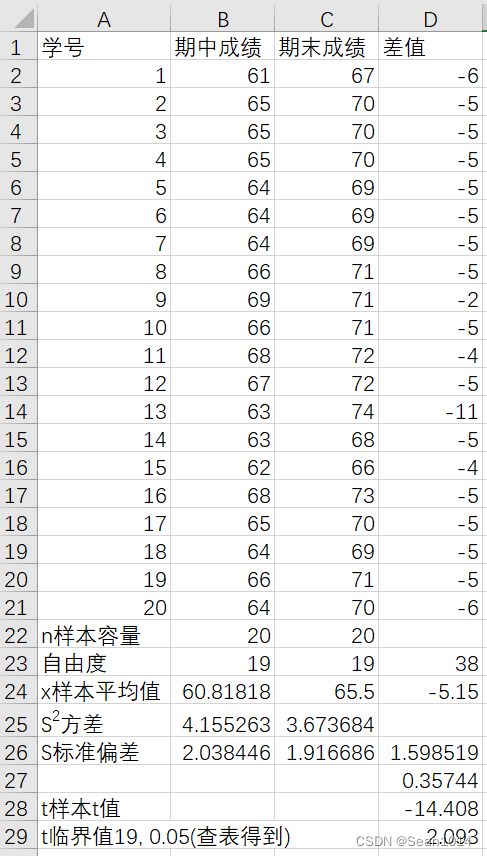显示公式 显示结果

因为是双尾检验，t值绝对值14.408>2.093，说明t值落在了95%置信区间以外。可以认为样本与总体存在显著差异。 

方法2：数据分析法

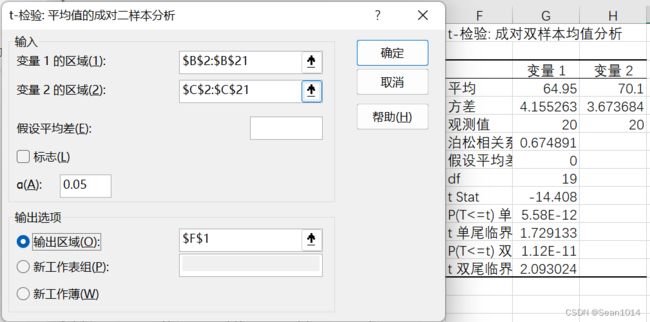
【操作】数据-数据分析（需要在加载项里打开“分析工具库”）-t-检验：平均值的成对二样本分析

选择输入变量的区域，选择输出区域

对比方法1和方法2，过程量求出的值一样。

因为是双尾检验，t值绝对值14.408>2.093，说明t值落在了95%置信区间以外。可以认为样本与总体存在显著差异。

SPSS

第一步：录入数据

  

第二步：分析-描述统计-探索，因变量成绩，因子考试，图-含莱文检验的分布-水平图-未转换，继续，确定。结果显示通过检验。

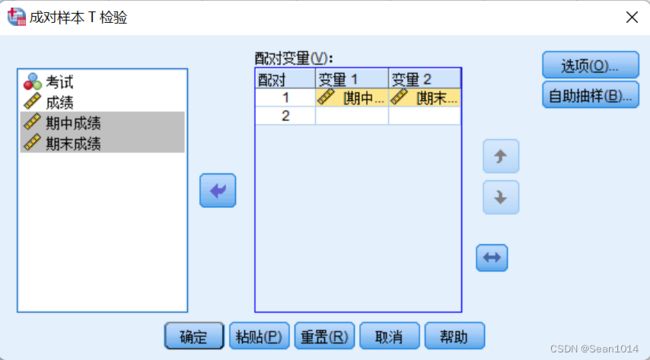
第三步：分析-比较平均值-成对样本T检验

Ctrl选中两次考试成绩，选入配对变量中，确定

 

第四步：查看配对样本检验表

t=-14.408，与用Excel计算的结果一致。

P为0.000<0.05，拒绝H0，接受H1，认为两次成绩差异显著。

R语言

install.packages("dplyr")
library("dplyr")
A<-c(61,65,65,65,64,64,64,66,69,66,68,67,63,63,62,68,65,64,66,64)
B<-c(67,70,70,70,69,69,69,71,71,71,72,72,74,68,66,73,70,69,71,70)
res <- t.test(A,B,paired = TRUE,alternative = "two.sided")

结果如下：

有2种判断结果的方法

1. 看t值，t=-14.408，查表可知t临界值19, 0.05为2.093，判断样本与总体存在显著差异。

2. 看P值，p-value = 1.115e-11<0.05，判断样本与总体存在显著差异。