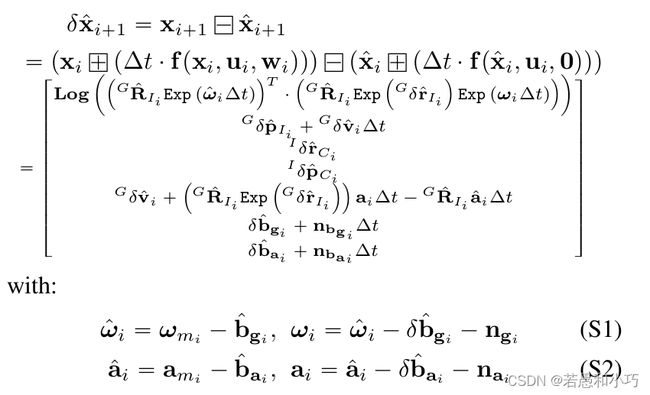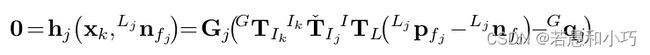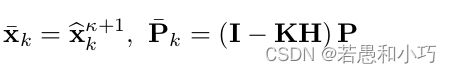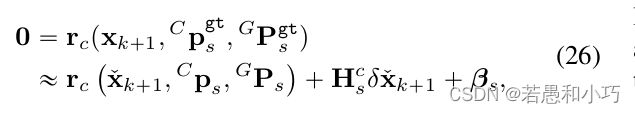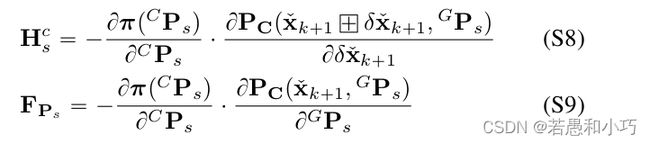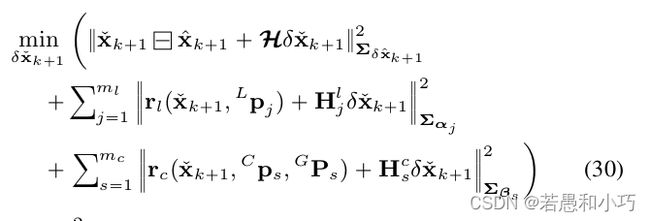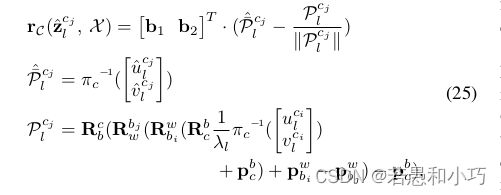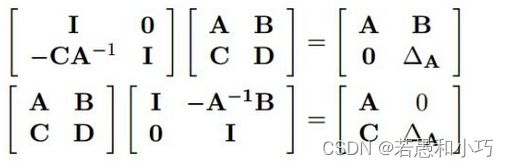R3Live系列学习（四）R2Live源码阅读（2）

（万字长文预警）

这段时间换了部门，有许多要交接的事情要忙，并且设计开发了一个大型的视觉地图养成系统，非常有意思乃至于废寝忘食，所以文章鸽了很久，这一篇克服拖延症，将r2live的阅读写完。

不得不说，我在阅读的过程当中并没有抠太多数学上的细节，没有去深入思考四元数的表述形式，李代数是求导还是扰动，公式之间结果的跳变，或是代码和公式有些地方对不上等等，更注重如何剖析整个工程，站在作者的角度去“逆向开发”，并思考如何将这样的思路应用到自己的学习与工作当中，如果大家在工作中遇到类似的需求，会想到“可以从这个思路上尝试”，或者在从写公式和代码的转化中获取经验和借鉴，那我们的时间就没有浪费。随着时间推移，这样的偏设计和工程的思维方式也在转型，正在和大家一起成长进步。

那么，r2live的状态估计依然是采取ESKF的方式，这部分一直都是大多数人（像我这种蠢人）的痛点。在这里真诚推荐一本“中篇小说”《Quaternion kinematics for the error state KF》，它确实能够成为本系列博客乃至多传感器融合领域的一种预备知识。

适用该工程的激光传感器还是livox雷达，对于lidar特征的提取已经在loam-livox的解读中研究得比较多了，在这里不再赘述，只需要知道它位于r2live/src/fast_lio/feature_extract.cpp中即可，它是一个独立的进程，只做特征提取，发布的话题是角点、面点、全部点。在这个工程里，对lidar特征和imu数据的处理都在estimator的process线程里实现，但是文件放在fast-lio文件夹里，千万不要看岔了。

工程的总驱动在estimator_node.cpp，它包含了r2live的main函数，同时也声明了一些全局变量，它们非常重要：

a、全局变量

Camera_Lidar_queue g_camera_lidar_queue;
MeasureGroup Measures;
StatesGroup g_lio_state;

 它们声明在文件开头，同时也是被fast_lio.hpp所共享的，关键的状态量与观测量用全局变量分享。

b、main函数

if (estimator.m_fast_lio_instance == nullptr)
{
    estimator.m_fast_lio_instance = new Fast_lio();
}
registerPub(nh);

ros::Subscriber sub_imu = nh.subscribe(IMU_TOPIC, 20000, imu_callback, ros::TransportHints().tcpNoDelay());
ros::Subscriber sub_image = nh.subscribe("/feature_tracker/feature", 20000, feature_callback, ros::TransportHints().tcpNoDelay());
ros::Subscriber sub_restart = nh.subscribe("/feature_tracker/restart", 20000, restart_callback, ros::TransportHints().tcpNoDelay());
ros::Subscriber sub_relo_points = nh.subscribe("/pose_graph/match_points", 20000, relocalization_callback, ros::TransportHints().tcpNoDelay());

std::thread measurement_process{process};
ros::spin();

estimator的main函数大致如上，它发布了很多可视化的相关话题（里程计位姿等），收取的话题是imu数据。另外，初始化了Fast_lio类的实例，在这个类里面，它也在收发话题数据，同时也接收了同一来源的imu数据！

了解该工程的同学都能感受到，主函数的运行其实是两个线程来回调用全局变量（状态量），用上一个状态量作为下一次估计的先验，vio与lio交替运行。这样的方式是有效粗暴的，我们分别阅读vio与lio的实现，再将它们串在一起，了解整个过程。

一、FAST-LIO

Fast_lio的实现主要包括callback函数和process线程，与fast-lio的原作一样，这里接收来自feature_extract发布的面点数据，以及imu，接收完之后装入队列中待处理，主要看process函数。

//在循环最后象征性的sleep一下
ros::Rate rate(5000);
bool status = ros::ok();
//将装载面特征的deque指针赋给vio和lio共享的全局变量
g_camera_lidar_queue.m_liar_frame_buf = &lidar_buffer;
while (ros::ok())
{
    if (flg_exit)
        break;
    ros::spinOnce();//一个象征性的spin

    std::this_thread::sleep_for(std::chrono::milliseconds(1));
    //由于我们规定相机数据要先于lidar数据处理，因此当lidar时间戳大于camera时间戳时，将在此等待
    while (g_camera_lidar_queue.if_lidar_can_process() == false)
    {
        // scope_color(ANSI_COLOR_YELLOW_BOLD);
        // cout << "Wait camera queue" << endl;
        std::this_thread::sleep_for(std::chrono::milliseconds(1));
    }
    // while (sync_packages(Measures))
    //使本线程的lio处理与estimator的vio处理互斥
    std::unique_lock lock(m_mutex_lio_process);
    if(1)
    {
        //收取同时段的lidar与imu信息，同时imu要多出一点以便插值
         if(sync_packages(Measures)==0)
         {
              continue;
         }
        //这是个一次性变量，与estimator相耦合，检查estimator的process线程有没有准备好
         if(g_camera_lidar_queue.m_if_lidar_can_start== 0)
         {   
              continue;
         }

    ......

开头这一段是对不同传感器的数据同步以及流程上的同步。由于imu频率高于camera，远高于lidar，因此设定camera先于lidar进行处理，合乎先验与更新的原理。

imu消息已在imu的callback函数中用队列不断装载并做好了时间同步，因此在process函数中拿两帧雷达数据之间的imu数据做去畸变处理，这一项在loam-livox那一章中已经读过。除了去畸变还做了预积分与推断状态转移方程。

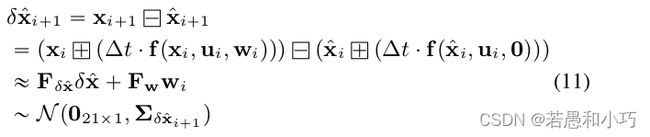
p_imu->Process(Measures, g_lio_state, feats_undistort);

state_inout = imu_preintegration(state_inout, v_imu, 1, end_pose_dt);

 复习一下FAST-LIO的相关公式内容，ESKF误差状态量的递推公式如下：

下一时刻的误差状态为本时刻的误差转移矩阵乘本时刻的误差状态，再加上噪声。具体的公式推导太多了写不过来，可以看下如下所示的r2live附录部分，也可以学习一下高博的简明ESKF推导简明ESKF推导 - 知乎。但整个推导过程不难理解，大家只需要将状态量的变化过程套给误差量的变化过程，同时忽略名义状态变量的噪声影响，因为ESKF的思想是将噪声加在误差量中。

 

获知了误差量的递推方程后再看到ImuProcess::imu_preintegration函数中的对应部分，由于imu积分是ESKF的预测部分，因此上一回合的误差的后验估计经过上面的递推公式后就成为了这一回合的先验，同时更新误差量的协方差矩阵。下面代码里的“平均值”指的是两个回合之间imu首尾数据的均值，再除去上一时刻的bias得到的“纯净值”。一般在ESKF当中，误差值在每次更新以后会被重置，因此只计算误差状态的协方差矩阵。

/* covariance propagation */
    Eigen::Matrix3d acc_avr_skew;
    Eigen::Matrix3d Exp_f = Exp(angvel_avr, dt);
    acc_avr_skew << SKEW_SYM_MATRX(acc_avr);
    // Eigen::Matrix3d Jr_omega_dt = right_jacobian_of_rotion_matrix(angvel_avr*dt);
    Eigen::Matrix3d Jr_omega_dt = Eigen::Matrix3d::Identity();
    F_x.block<3, 3>(0, 0) = Exp_f.transpose();
    // F_x.block<3, 3>(0, 9) = -Eye3d * dt;
    F_x.block<3, 3>(0, 9) = -Jr_omega_dt * dt;
    // F_x.block<3,3>(3,0)  = -R_imu * off_vel_skew * dt;
    F_x.block<3, 3>(3, 3) = Eye3d; // Already the identity.
    F_x.block<3, 3>(3, 6) = Eye3d * dt;
    F_x.block<3, 3>(6, 0) = -R_imu * acc_avr_skew * dt;
    F_x.block<3, 3>(6, 12) = -R_imu * dt;
    F_x.block<3, 3>(6, 15) = Eye3d * dt;

    Eigen::Matrix3d cov_acc_diag, cov_gyr_diag, cov_omega_diag;
    cov_omega_diag = Eigen::Vector3d(COV_OMEGA_NOISE_DIAG, COV_OMEGA_NOISE_DIAG, COV_OMEGA_NOISE_DIAG).asDiagonal();
    cov_acc_diag = Eigen::Vector3d(COV_ACC_NOISE_DIAG, COV_ACC_NOISE_DIAG, COV_ACC_NOISE_DIAG).asDiagonal();
    cov_gyr_diag = Eigen::Vector3d(COV_GYRO_NOISE_DIAG, COV_GYRO_NOISE_DIAG, COV_GYRO_NOISE_DIAG).asDiagonal();
    // cov_w.block<3, 3>(0, 0) = cov_omega_diag * dt * dt;
    cov_w.block<3, 3>(0, 0) = Jr_omega_dt * cov_omega_diag * Jr_omega_dt * dt * dt;
    cov_w.block<3, 3>(3, 3) = R_imu * cov_gyr_diag * R_imu.transpose() * dt * dt;
    cov_w.block<3, 3>(6, 6) = cov_acc_diag * dt * dt;
    cov_w.block<3, 3>(9, 9).diagonal() = Eigen::Vector3d(COV_BIAS_GYRO_NOISE_DIAG, COV_BIAS_GYRO_NOISE_DIAG, COV_BIAS_GYRO_NOISE_DIAG) * dt * dt; // bias gyro covariance
    cov_w.block<3, 3>(12, 12).diagonal() = Eigen::Vector3d(COV_BIAS_ACC_NOISE_DIAG, COV_BIAS_ACC_NOISE_DIAG, COV_BIAS_ACC_NOISE_DIAG) * dt * dt;  // bias acc covariance

    state_inout.cov = F_x * state_inout.cov * F_x.transpose() + cov_w;

    R_imu = R_imu * Exp_f;
    acc_imu = R_imu * acc_avr - state_inout.gravity;
    pos_imu = pos_imu + vel_imu * dt + 0.5 * acc_imu * dt * dt;
    vel_imu = vel_imu + acc_imu * dt;
    angvel_last = angvel_avr;
    acc_s_last = acc_imu;

继续看process函数，接下来是求点到面icp的过程，这一段和fast-lio以及livox系列的点云处理比较相似，用pca主成分分析进行平面提取，再将面点相互匹配，为的是建立观测关系，这一段也不再赘述。

lasermap_fov_segment();

/*** downsample the features of new frame ***/
downSizeFilterSurf.setInputCloud(feats_undistort);
downSizeFilterSurf.filter(*feats_down);

随后是IEKF的实现，先给出一个迭代周期的大致流程：

1.计算平面的参数方程ax+by+cz+d=0

2.将计算得到的平面与上一帧的平面点互相匹配得到认为是同一个平面，即位姿变换的观测量

3.以imu积分为先验作EKF更新

4.更新协方差，得到误差的最优估计以及真正的状态向量

在这里的状态向量都是误差，也就是当误差变化收敛后再得到真正的状态量。状态空间是误差量：
  

接下来结合代码看一下预测和更新过程。

我们按本帧的对应点面数建立观测方程：

观测方程对误差量的雅克比矩阵H是求解增益K的必要分子，而观测量（点面距离）对误差状态的偏导数可以按链式法则转换为观测量对名义状态的偏导数乘名义状态对误差状态的偏导数。

Eigen::MatrixXd Hsub(laserCloudSelNum, 6);
Eigen::VectorXd meas_vec(laserCloudSelNum);
Hsub.setZero();

// omp_set_num_threads(4);
// #pragma omp parallel for
for (int i = 0; i < laserCloudSelNum; i++)
{
    const PointType &laser_p = laserCloudOri->points[i];
    Eigen::Vector3d point_this(laser_p.x, laser_p.y, laser_p.z);
    point_this += Lidar_offset_to_IMU;
    Eigen::Matrix3d point_crossmat;
    point_crossmat << SKEW_SYM_MATRX(point_this);

    /*** get the normal vector of closest surface/corner ***/
    const PointType &norm_p = coeffSel->points[i];
    Eigen::Vector3d norm_vec(norm_p.x, norm_p.y, norm_p.z);

    /*** calculate the Measuremnt Jacobian matrix H ***/
    Eigen::Vector3d A(point_crossmat * g_lio_state.rot_end.transpose() * norm_vec);
    Hsub.row(i) << VEC_FROM_ARRAY(A), norm_p.x, norm_p.y, norm_p.z;

    /*** Measuremnt: distance to the closest surface/corner ***/
    meas_vec(i) = -norm_p.intensity;
}

上面的一段可以看做是求取观测雅克比矩阵H和观测量z的过程，注释也写的比较明白，而接下来的一段是在求解增益矩阵K之后，再得到误差量的后验，进而计算其变化量，当变化量小于阈值时判断其收敛。

Eigen::Vector3d rot_add, t_add, v_add, bg_add, ba_add, g_add;
Eigen::Matrix solution;
Eigen::MatrixXd K(DIM_OF_STATES, laserCloudSelNum);

/*** Iterative Kalman Filter Update ***/
if (!flg_EKF_inited)
{
    cout << ANSI_COLOR_RED_BOLD << "Run EKF init" << ANSI_COLOR_RESET << endl;
    /*** only run in initialization period ***/
    Eigen::MatrixXd H_init(Eigen::Matrix::Zero());
    Eigen::MatrixXd z_init(Eigen::Matrix::Zero());
    H_init.block<3, 3>(0, 0) = Eigen::Matrix3d::Identity();
    H_init.block<3, 3>(3, 3) = Eigen::Matrix3d::Identity();
    H_init.block<3, 3>(6, 15) = Eigen::Matrix3d::Identity();
    z_init.block<3, 1>(0, 0) = -Log(g_lio_state.rot_end);
    z_init.block<3, 1>(0, 0) = -g_lio_state.pos_end;

    auto H_init_T = H_init.transpose();
    auto &&K_init = g_lio_state.cov * H_init_T * (H_init * g_lio_state.cov * H_init_T + 0.0001 * Eigen::Matrix::Identity()).inverse();
    solution = K_init * z_init;

    solution.block<9, 1>(0, 0).setZero();
    g_lio_state += solution;
    g_lio_state.cov = (Eigen::MatrixXd::Identity(DIM_OF_STATES, DIM_OF_STATES) - K_init * H_init) * g_lio_state.cov;
}
else
{
    // cout << ANSI_COLOR_RED_BOLD << "Run EKF uph" << ANSI_COLOR_RESET << endl;
    auto &&Hsub_T = Hsub.transpose();
    H_T_H.block<6, 6>(0, 0) = Hsub_T * Hsub;
    Eigen::Matrix &&K_1 =
        (H_T_H + (g_lio_state.cov / LASER_POINT_COV).inverse()).inverse();
    K = K_1.block(0, 0) * Hsub_T;

    // solution = K * meas_vec;
    // g_lio_state += solution;

    auto vec = state_propagat - g_lio_state;
    solution = K * (meas_vec - Hsub * vec.block<6, 1>(0, 0));
    g_lio_state = state_propagat + solution;
    // cout << ANSI_COLOR_RED_BOLD << "Run EKF uph, vec = " << vec.head<9>().transpose() << ANSI_COLOR_RESET << endl;

    rot_add = solution.block<3, 1>(0, 0);
    t_add = solution.block<3, 1>(3, 0);

    flg_EKF_converged = false;

    if (((rot_add.norm() * 57.3 - deltaR) < 0.01) && ((t_add.norm() * 100 - deltaT) < 0.015))
    {
        flg_EKF_converged = true;
    }

    deltaR = rot_add.norm() * 57.3;
    deltaT = t_add.norm() * 100;
}
euler_cur = RotMtoEuler(g_lio_state.rot_end);

 

 当IESKF结束退出的时候更新后验的协方差矩阵，其实最重要的还是这个协方差矩阵，它决定了下一时刻的误差量迭代！

if (rematch_num >= 2 || (iterCount == NUM_MAX_ITERATIONS - 1)) // Fast lio ori version.
{
    if (flg_EKF_inited)
    {
        /*** Covariance Update ***/
        G.block(0, 0) = K * Hsub;
        g_lio_state.cov = (I_STATE - G) * g_lio_state.cov;
        total_distance += (g_lio_state.pos_end - position_last).norm();
        position_last = g_lio_state.pos_end;

        // std::cout << "position: " << g_lio_state.pos_end.transpose() << " total distance: " << total_distance << std::endl;
    }
    solve_time += omp_get_wtime() - solve_start;
    break;
}

  在完成本次状态估计后，将新的帧中的一些点云加入到kd树中，更新下一帧在地图中查找的依据。

ikdtree.Add_Points(feats_down_updated->points, true);

抛开状态量先验的来源不谈，整个过程其实和FAST-LIO大体相同，通过若干次迭代（其中重新构造观测点和面的对应关系）逼近结果。

二、estimator

estimator_node.cpp主要是VIO的实现，看到process函数。在函数开始的部分对fast-lio与本线程做了数据与处理的同步与互斥，这更清晰地说明了两者的接力关系：

if (estimator.m_fast_lio_instance != nullptr)
{
    g_camera_lidar_queue.m_camera_imu_td = estimator.td;
    g_camera_lidar_queue.m_last_visual_time = img_msg->header.stamp.toSec();

    //相同地，我们规定相机数据要先于雷达数据处理，因此若有雷达数据未处理或没有等到下一帧图像则等待
    while (g_camera_lidar_queue.if_camera_can_process() == false)
    {
         std::this_thread::sleep_for(std::chrono::milliseconds(1));
    }

    //锁住fast-lio使两边的处理互斥
    lock_lio(estimator);
    t_s.tic();
    double camera_LiDAR_tim_diff = img_msg->header.stamp.toSec() + g_camera_lidar_queue.m_camera_imu_td - g_lio_state.last_update_time;
    //将fast-lio处理完毕的imu状态在本函数内继续处理
    *p_imu = *(estimator.m_fast_lio_instance->m_imu_process);
}

因此在imu数据插值并预积分到对齐图像帧的时间戳之后， 开始正式计算vio。下一段是异常处理，针对lio与vio状态差距过大的情况，也就是发散了，或者遇到了剧烈运动，将重启vio系统，直接将VIO的滑动窗口内的状态量掰向LIO，使其强行对齐。

if (imu_queue.size())
{
    if (g_lio_state.last_update_time == 0)
    {
        g_lio_state.last_update_time = imu_queue.front()->header.stamp.toSec();
    }
    /// 
    double start_dt = g_lio_state.last_update_time - imu_queue.front()->header.stamp.toSec();
    double end_dt = cam_update_tim - imu_queue.back()->header.stamp.toSec();
    esikf_update_valid = true;
    if (g_camera_lidar_queue.m_if_have_lidar_data && (estimator.solver_flag == Estimator::SolverFlag::NON_LINEAR))
    {
        *p_imu = *(estimator.m_fast_lio_instance->m_imu_process);
        state_aft_integration = p_imu->imu_preintegration(g_lio_state, imu_queue, 0, cam_update_tim - imu_queue.back()->header.stamp.toSec());
        estimator.m_lio_state_prediction_vec[WINDOW_SIZE] = state_aft_integration;
        
        /// 
        diff_vins_lio_q = eigen_q(estimator.Rs[WINDOW_SIZE].transpose() * state_aft_integration.rot_end);
        diff_vins_lio_t = state_aft_integration.pos_end - estimator.Ps[WINDOW_SIZE];
        if (diff_vins_lio_t.norm() > 1.0)
        {
            // ROS_INFO("VIO subsystem restart ");
            /// 
            estimator.refine_vio_system(diff_vins_lio_q, diff_vins_lio_t);
            diff_vins_lio_q.setIdentity();
            diff_vins_lio_t.setZero();
        }
        if ((start_dt > -0.02) &&
            (fabs(end_dt) < 0.02))
        {
            g_lio_state = state_aft_integration;
            g_lio_state.last_update_time = cam_update_tim;
        }
        else
        {
            // esikf_update_valid = false;
            ...
        }
    }
}

在feature节点的特征点信息都将会用作判断关键帧与边缘化策略，这个在各种滑窗法都相似。

//预处理，通过视差判断是否为关键帧，是采取何种边缘化的方法，即新帧与上一帧视差大则边缘化最老帧，视差小就边缘化上一帧，狠合理
estimator.processImage(image, img_msg->header);

 随后重点来了，如何理解r2live论文中的式26~30？同样是ESKF的思想，式26说明对于真值而言，观测量、状态量和路标点的残差为0，因此在零点附近对误差（△x）做一阶泰勒展开，展开点为当前估计的状态量。其中Cps指的是特征点像素坐标，GPs指的是特征点的世界坐标系下的坐标。

式27~29的含义就是观测量对误差量的雅克比矩阵，以及高阶项（噪声量）的协方差矩阵与转移公式。

r2live论文的附录E中解释了观测量对误差状态的雅克比矩阵的求法，与FAST-LIO中一样是采取链式求导：

 论文中解释说， 整个r2live的误差函数包括了系统先验、雷达的观测量、相机的观测量，它们共同组成了系统的误差。而式30的第三项就是视觉项的误差，在我看来，在一个周期内，整个误差函数的更新是先计算一、三项，再用最优估计量去计算第二项。这样的做法综合考虑了传感器的不同特性和代码的耦合性。

 

对应求解公式30的主要部分就在接下来这段，在construct_camera_measure函数中，重新构建了残差函数与观测量，以及观测量对误差量的雅克比矩阵，从而进行迭代，求解方法和上一节大致相同。

/// 按imu先验的位姿，将一个点的所有观测一起加入三角化的计算，相当于得到了新加入特征点的先验
estimator.f_manager.triangulate(estimator.Ps, estimator.tic, estimator.ric);

double deltaR = 0, deltaT = 0;
int flg_EKF_converged = 0;
Eigen::Matrix solution;
Eigen::Vector3d rot_add, t_add, v_add, bg_add, ba_add, g_add;

std::vector pts_i, pts_j;
std::vector> reppro_err_vec;
std::vector, Eigen::aligned_allocator>> J_mat_vec;
Eigen::Matrix Hsub;
Eigen::Matrix meas_vec;
int win_idx = WINDOW_SIZE;

Eigen::Matrix K;
Eigen::Matrix K_1;
for (int iter_time = 0; iter_time < 2; iter_time++)
{
    /// 每次迭代开始，上一次vio结束优化后的位姿，都作为初值
    Eigen::Quaterniond q_pose_last = Eigen::Quaterniond(state_aft_integration.rot_end * diff_vins_lio_q.inverse());
    Eigen::Vector3d t_pose_last = state_aft_integration.pos_end - diff_vins_lio_t;
    estimator.m_para_Pose[win_idx][0] = t_pose_last(0);
    estimator.m_para_Pose[win_idx][1] = t_pose_last(1);
    estimator.m_para_Pose[win_idx][2] = t_pose_last(2);
    estimator.m_para_Pose[win_idx][3] = q_pose_last.x();
    estimator.m_para_Pose[win_idx][4] = q_pose_last.y();
    estimator.m_para_Pose[win_idx][5] = q_pose_last.z();
    estimator.m_para_Pose[win_idx][6] = q_pose_last.w();
    // estimator.f_manager.removeFailures();

    /// 重新计算在一个窗口内，一个特征点在最新的观测帧与在窗口中最老的一帧，这两帧对应的imu位姿，将这两帧做重投影误差建立残差关系
    construct_camera_measure(win_idx, estimator, reppro_err_vec, J_mat_vec);
    cout << "reppro_err_vec : " << reppro_err_vec.size() << "\n";
    if (reppro_err_vec.size() < minmum_number_of_camera_res)
    {
        cout << "Size of reppro_err_vec: " << reppro_err_vec.size() << endl;
        break;
    }
    
    // TODO: Add camera residual here
    Hsub.resize(reppro_err_vec.size() * 2, 6);
    meas_vec.resize(reppro_err_vec.size() * 2, 1);
    K.resize(DIM_OF_STATES, reppro_err_vec.size());
    int features_correspondences = reppro_err_vec.size();
    
    for (int residual_idx = 0; residual_idx < reppro_err_vec.size(); residual_idx++)
    {
        meas_vec.block(residual_idx * 2, 0, 2, 1) = -1 * reppro_err_vec[residual_idx];
        // J_mat_vec[residual_idx].block(0,0,2,3) = J_mat_vec[residual_idx].block(0,0,2,3) * extrinsic_vins_lio_q.toRotationMatrix().transpose();
        Hsub.block(residual_idx * 2, 0, 2, 6) = J_mat_vec[residual_idx];
    }

    K_1.setZero();
    auto Hsub_T = Hsub.transpose();

    H_T_H.setZero();
    H_T_H.block<6, 6>(0, 0) = Hsub_T * Hsub;
    K_1 = (H_T_H + (state_aft_integration.cov * CAM_MEASUREMENT_COV).inverse()).inverse();
    K = K_1.block(0, 0) * Hsub_T;
    auto vec = state_prediction - state_aft_integration;
    solution = K * (meas_vec - Hsub * vec.block<6, 1>(0, 0) );

    mean_reprojection_error = abs(meas_vec.mean());

    if (std::isnan(solution.sum()))
    {
        break;
    }

    state_aft_integration = state_prediction + solution;
    solution = state_aft_integration - state_prediction;

    rot_add = (solution).block<3, 1>(0, 0);
    t_add = solution.block<3, 1>(3, 0);
    flg_EKF_converged = false;
    if (((rot_add.norm() * 57.3 - deltaR) < 0.01) && ((t_add.norm()  - deltaT) < 0.015))
    {
        flg_EKF_converged = true;
    }
    deltaR = rot_add.norm() * 57.3;
    deltaT = t_add.norm() ;
}

但在算完之后，lio的状态量告一段落，将最新的状态量赋给vio最新的一帧，接下来又开始计算vio的滑动窗口内所有的状态量，用最新的ESKF的后验去更新滑窗，似乎这个滑窗是独立于lio的状态，只是为ESKF提供合理的观测量，这是非常机智的做法，但更像是作者的权宜之计。

g_lio_state = state_before_esikf;
/// 需要重新三角化
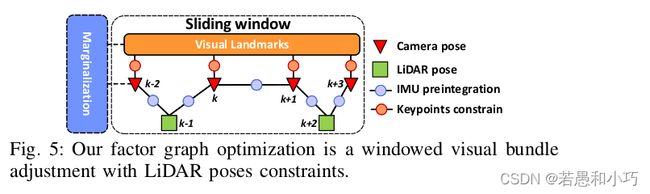
/// 对整个滑动窗口内的目标状态进行优化，加入优化的因子有：窗口内的imu预积分、每个点在每一个观测帧的重投影、窗口内每一帧的lio位姿            
estimator.solve_image_pose(img_msg->header);

 solve_image_pose函数就是论文第五部分（factor pose graph）的实现，维护滑动窗口的实现继承了vins-mono：

 在线初始化直接采用了vins系列的方法，先使用sfm算法对连续的一段时间的图像做位姿估计，然后采用imu积分与视觉位姿估计对齐的方式，得到粗略的尺度与重力方向，再精配准估计得到重力方向、bias、相机imu的外参与时间差，具体方法在此不再赘述。 初始化完毕后的视觉里程计向前递增的位姿计算，完全放入了optimization_LM函数。

void Estimator::solveOdometry()
{
    if (frame_count < WINDOW_SIZE)
        return;
    if (solver_flag == NON_LINEAR)
    {
        TicToc t_tri;
        f_manager.triangulate(Ps, tic, ric);
        ROS_DEBUG("triangulation costs %f", t_tri.toc());
        // ANCHOR - using optimization
        optimization_LM();
    }
}

 optimization_LM函数由于比较长，就不po整个代码段了。它在优化位姿的过程中使用了不同的因子（factor），其中包括vio中经典的imu预积分的因子，重投影因子，边缘化因子，另外还包括激光雷达的先验因子，我们一项一项地看：

①预积分因子

IMUFactor *imu_factor = new IMUFactor(pre_integrations[j]);
IMU_factor_res imu_factor_res;
imu_factor_res.add_keyframe_to_keyframe_factor(this, imu_factor, i, j);
imu_factor_res_vec.push_back(imu_factor_res);

简单po一下vins的公式，这个公式指代的是两个图像时刻内的状态量与预积分的残差，相对应的雅克比矩阵代码在factor文件夹下imu_factor.h，各自的位置对应写得很清楚，就不详细注释了，只要对着公式和代码就能看懂。

②特征点因子

ProjectionTdFactor *f_td = new ProjectionTdFactor(pts_i, pts_j, it_per_id.feature_per_frame[0].velocity, it_per_frame.velocity,
                                                              it_per_id.feature_per_frame[0].cur_td, it_per_frame.cur_td,
                                                              it_per_id.feature_per_frame[0].uv.y(), it_per_frame.uv.y());
Keypoint_projection_factor key_pt_projection_factor;
key_pt_projection_factor.add_projection_factor(this, f_td, imu_i, imu_j, feature_index);
projection_factor_res_vec.push_back(key_pt_projection_factor);

重投影误差的公式也非常熟悉了，我也照抄了vins的公式。重投影误差对状态量的偏导数求解位于projection_td_factor.cpp，在这里考虑了相机曝光时间和相机imu时间差，以及相机imu的外参，将尤其是前两项，需要考虑到前端的光流跟踪的特征点速度，这也是处心积虑保存速度的原因。

③lidar先验因子

LiDAR_prior_factor_15 *lidar_prior_factor = new LiDAR_prior_factor_15(&m_lio_state_prediction_vec[i]);
L_prior_factor l_prior_factor;
l_prior_factor.add_lidar_prior_factor(this, lidar_prior_factor, i);
lidar_prior_factor_vec.push_back(l_prior_factor);

在estimator_node.cpp里看到参与优化的状态量是每次lio优化完毕后的状态量再叠加预积分的量：

estimator.m_lio_state_prediction_vec[WINDOW_SIZE] = state_aft_integration;

 但是在残差和雅克比矩阵计算的时候，它只对窗口内的帧在预积分前的状态求了偏导数，残差的信息矩阵是直接采用了FAST-LIO计算后的协方差矩阵，那么预积分量只是补齐使得其它因子拥有同样的状态量Pi和Qi，并没有别的特别含义。因此加入lidar先验因子的目的还是使VIO进一步的贴合LIO轨迹，但看上去应该会有更好的解决方式。

  ④边缘化因子

在优化过程中也加入了边缘化因子，既然滑动窗口中未包括的帧要被剔除，但仍希望保留这些被踢出的帧对滑窗内的观测约束，那就要用这些观测约束构造一个先验加入优化，而基于FEJ（First Estimate Jacobians）原理，这个先验的雅克比不随迭代变化，因此在Evaluate函数中单独领出来求解。具体的残差与雅克比矩阵的计算在Marginalization_factor结构体的Evaluate_mine函数中，可以看到边缘化因子的雅克比矩阵是直接调用了上一次边缘化操作后的结果。

for (int i = 1; i < WINDOW_SIZE; i++)
{
    temp_t = Eigen::Vector3d(g_estimator->m_para_Pose[i][0], g_estimator->m_para_Pose[i][1], g_estimator->m_para_Pose[i][2]);
    temp_Q = Eigen::Quaterniond(g_estimator->m_para_Pose[i][6], g_estimator->m_para_Pose[i][3], g_estimator->m_para_Pose[i][4], g_estimator->m_para_Pose[i][5]).normalized();
    diff_x.block(pos, 0, 3, 1) = temp_t - Eigen::Vector3d(m_vio_margin_ptr->m_Ps[i + 1]);
    diff_x.block(pos + 3, 0, 3, 1) = Eigen::Vector3d(Sophus::SO3d(m_vio_margin_ptr->m_Rs[i + 1].transpose() * temp_Q.toRotationMatrix()).log());
    jacobian_matrix.block(0, i * 15, margin_residual_size, 6) = m_vio_margin_ptr->m_linearized_jacobians.block(0, pos, margin_residual_size, 6);
    pos += 6;
}

顺便也看看与经典VIO一脉相承的，滑动窗口法的边缘化操作，边缘化实现起来很直接，一方面是看被边缘的帧的情况将其它帧的数据补充到空位中，这个过程有点像冒泡排序；另一方面是将被边缘帧的残差带入下一轮的滑窗当中，保留一定的影响。

void Estimator::slideWindow()
{
    TicToc t_margin;
    if (marginalization_flag == MARGIN_OLD)
    {
        double t_0 = Headers[0].stamp.toSec();
        back_R0 = Rs[0];
        back_P0 = Ps[0];
        if (frame_count == WINDOW_SIZE)
        {
            for (int i = 0; i < WINDOW_SIZE; i++)
            {
                Rs[i].swap(Rs[i + 1]);

                std::swap(pre_integrations[i], pre_integrations[i + 1]);

                dt_buf[i].swap(dt_buf[i + 1]);
                linear_acceleration_buf[i].swap(linear_acceleration_buf[i + 1]);
                angular_velocity_buf[i].swap(angular_velocity_buf[i + 1]);

                Headers[i] = Headers[i + 1];
                Ps[i].swap(Ps[i + 1]);
                Vs[i].swap(Vs[i + 1]);
                Bas[i].swap(Bas[i + 1]);
                Bgs[i].swap(Bgs[i + 1]);
                std::swap( m_lio_state_prediction_vec[i] ,  m_lio_state_prediction_vec[i + 1] ) ;
            }
            Headers[WINDOW_SIZE] = Headers[WINDOW_SIZE - 1];
            Ps[WINDOW_SIZE] = Ps[WINDOW_SIZE - 1];
            Vs[WINDOW_SIZE] = Vs[WINDOW_SIZE - 1];
            Rs[WINDOW_SIZE] = Rs[WINDOW_SIZE - 1];
            Bas[WINDOW_SIZE] = Bas[WINDOW_SIZE - 1];
            Bgs[WINDOW_SIZE] = Bgs[WINDOW_SIZE - 1];
            m_lio_state_prediction_vec[WINDOW_SIZE] = m_lio_state_prediction_vec[WINDOW_SIZE-1];

            delete pre_integrations[WINDOW_SIZE];
            pre_integrations[WINDOW_SIZE] = new IntegrationBase{acc_0, gyr_0, Bas[WINDOW_SIZE], Bgs[WINDOW_SIZE]};

            dt_buf[WINDOW_SIZE].clear();
            linear_acceleration_buf[WINDOW_SIZE].clear();
            angular_velocity_buf[WINDOW_SIZE].clear();

            if (true || solver_flag == INITIAL)
            {
                map::iterator it_0;
                it_0 = m_all_image_frame.find(t_0);
                delete it_0->second.pre_integration;
                it_0->second.pre_integration = nullptr;
 
                for (map::iterator it = m_all_image_frame.begin(); it != it_0; ++it)
                {
                    if (it->second.pre_integration)
                        delete it->second.pre_integration;
                    it->second.pre_integration = NULL;
                }

                m_all_image_frame.erase(m_all_image_frame.begin(), it_0);
                m_all_image_frame.erase(t_0);

            }
            slideWindowOld();
        }
    }
    else
    {
        if (frame_count == WINDOW_SIZE)
        {
            for (unsigned int i = 0; i < dt_buf[frame_count].size(); i++)
            {
                double tmp_dt = dt_buf[frame_count][i];
                Vector3d tmp_linear_acceleration = linear_acceleration_buf[frame_count][i];
                Vector3d tmp_angular_velocity = angular_velocity_buf[frame_count][i];

                pre_integrations[frame_count - 1]->push_back(tmp_dt, tmp_linear_acceleration, tmp_angular_velocity);

                dt_buf[frame_count - 1].push_back(tmp_dt);
                linear_acceleration_buf[frame_count - 1].push_back(tmp_linear_acceleration);
                angular_velocity_buf[frame_count - 1].push_back(tmp_angular_velocity);
            }

            Headers[frame_count - 1] = Headers[frame_count];
            Ps[frame_count - 1] = Ps[frame_count];
            Vs[frame_count - 1] = Vs[frame_count];
            Rs[frame_count - 1] = Rs[frame_count];
            Bas[frame_count - 1] = Bas[frame_count];
            Bgs[frame_count - 1] = Bgs[frame_count];
            m_lio_state_prediction_vec[frame_count - 1] = m_lio_state_prediction_vec[frame_count];

            delete pre_integrations[WINDOW_SIZE];
            pre_integrations[WINDOW_SIZE] = new IntegrationBase{acc_0, gyr_0, Bas[WINDOW_SIZE], Bgs[WINDOW_SIZE]};

            dt_buf[WINDOW_SIZE].clear();
            linear_acceleration_buf[WINDOW_SIZE].clear();
            angular_velocity_buf[WINDOW_SIZE].clear();

            slideWindowNew();
        }
    }
}

边缘化操作的核心代码在vio_marginalization.hpp的marginalize函数。信息矩阵A需要边缘化下标为m的帧，采用的是舒尔补的方法：

 使得Ax=b的上半部分被消去，从而得到新的信息矩阵，而边缘化的帧带来的先验，它在求雅克比矩阵时将会被固定住，不随迭代变化而改变线性化的点，这就是FEJ的由来。

Eigen::MatrixXd Amm_inv, Amm;
Eigen::MatrixXd A, b;
// Amm = res_hessian.block( 0, 0, m, m );
Amm = 0.5 * (res_hessian.block(0, 0, m, m) + res_hessian.block(0, 0, m, m).transpose());
// Amm_inv = Amm.fullPivHouseholderQr().solve(Imm);
// Amm_inv = Amm.colPivHouseholderQr().solve(Imm);
Amm_inv = Amm.ldlt().solve( Eigen::MatrixXd::Identity( m, m ) );

Eigen::SparseMatrix< double > bmm = res_residual.segment( 0, m ).sparseView();
Eigen::SparseMatrix< double > Amr = res_hessian.block( 0, m, m, n ).sparseView();
Eigen::SparseMatrix< double > Arm = res_hessian.block( m, 0, n, m ).sparseView();
Eigen::SparseMatrix< double > Arr = res_hessian.block( m, m, n, n ).sparseView();
Eigen::SparseMatrix< double > brr = res_residual.segment( m, n ).sparseView();
// t_thread_summing.tic();
// Eigen::SparseMatrix Arm_Amm_inv = Arm * (Amm_inv.sparseView());
Eigen::SparseMatrix< double > Amm_inv_spm = Amm_inv.sparseView();
Eigen::SparseMatrix< double > Arm_Amm_inv = ( Arm ) *Amm_inv_spm;

A = ( Arr - Arm_Amm_inv * Amr ).toDense();
b = ( brr - Arm_Amm_inv * bmm ).toDense();
m_linearized_jacobians = A.llt().matrixL().transpose();

 综上所述，几个因子都得到了残差相对于状态量的雅克比矩阵，接下来是求状态量，用的是LM法，它相对于高斯牛顿法多了一个信赖区间，当然我们在这里也可以将它当做黑盒，知道最后通过迭代求得了这一轮的新状态量。这些因子都继承的是ceres::SizedCostFunction，最终却没有用ceres去优化，可能只是单纯想用LM法求解吧。

Eigen::SparseMatrix residual_sparse, jacobian_sparse, hessian_sparse;
LM_trust_region_strategy lm_trust_region;
for (int iter_count = 0; iter_count < NUM_ITERATIONS + g_extra_iterations; iter_count++)
{
    t_build_cost += timer_tictoc.toc();
    timer_tictoc.tic();
    Evaluate(this, imu_factor_res_vec, projection_factor_res_vec, lidar_prior_factor_vec, margin_factor, feature_index, jacobian_sparse, residual_sparse);
    Eigen::VectorXd delta_vector;
    //delta_vector = solve_LM(jacobian_sparse, residual_sparse);
    delta_vector = lm_trust_region.compute_step(jacobian_sparse, residual_sparse, (WINDOW_SIZE + 1) * 15 + 6 + 1).toDense();
    update_delta_vector(this, delta_vector);
    t_LM_cost += timer_tictoc.toc();
}

看到最后可以发现，r2live的产出终究还是雷达惯导里程计计算之后生成的点云，而不同的里程计模块计算得到的轨迹也是相对独立的，起到“点缀的作用”，或者说是兜底的作用。

可以得知，比较起FAST-LIO的计算精度，r2live提升程度不大，能感觉到视觉约束对精度影响的边界效应（毕竟在好的场景下FAST-LIO已经蛮准了）。但在激光里程计退化的情况下，视觉能够提供良好的补偿，进一步提升了鲁棒性。可以认为，r2live是偏工程化的作品，它生成的点云实际上还是用于后期定位而非观赏，但这绝不是否认它的价值，事物都是螺旋上升迭代发展的，这个工程庞大的代码量在开发调试的过程中肯定充斥着坎坷，光看完它就费了我很多业余时间，可见作者团队的深厚实力与积淀。

再举个不恰当的栗子，SFM算法生成的点云如果作为观赏或MVS算法的种子点，它需要小心地不断滤去错误点同时恢复BA优化后被误删的约束，以保证种子点的多样性和纯洁性，但若只是想用来做视觉定位，则完全可以更粗鲁地对待它。如果多传感器融合的方式像r2live这样定好，我们完全可以改造它，向里面加入更多的传感器信息对地图的精度精益求精，但在外行看来，这两幅地图可能并没有太大的差别，这就牵扯到带纹理与不带纹理的地图在业务上或者说在产品层次上的竞争力差别了，毕竟甲方肯定希望购买的产品特性越多越强还便宜，如果一张地图能够用来观赏或其他用途，那它就绝不会只拿来做定位。

另一方面，如果有一种像素级别的约束可以进一步提升精度，而无需精确标定曝光，计算消耗也能接受的话，它肯定会是一种建图方法上新的启发。

下一篇我将学习r3live，以及带纹理点云的生成原理，绝对不鸽太久~