Self-Attention 原理与代码实现

1.Self-Attention 结构

        在计算的时候需要用到矩阵Q(查询),K(键值),V(值)。在实际中，Self-Attention 接收的是输入(单词的表示向量x组成的矩阵X) 或者上一个 Encoder block 的输出。而Q,K,V正是通过 Self-Attention 的输入进行线性变换得到的。

2. Q, K, V 的计算

        Self-Attention 的输入用矩阵X进行表示，使用线性变阵矩阵、、经过计算得到、、 计算如下图所示，注意 X, Q, K, V 的每一行都表示一个单词。

3.Self-Attention 的计算

3.1 计算公式

        得到矩阵 Q, K, V之后就可以计算 Self-Attention 的值了，计算的公式如下：

3.2 计算相关系数 

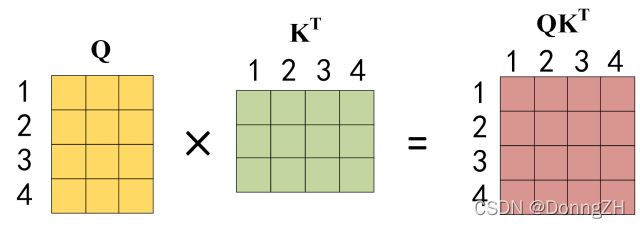
        公式中计算矩阵Q和K每一行向量的内积，为了防止内积过大，因此除以的平方根。*后，得到的矩阵行列数都为 ， 为句子单词数，这个矩阵可以表示单词之间的 attention 强度。

        得到 之后，使用Softmax对矩阵的每一行都进行归一化，计算当前单词相对于其他单词的相关系数（attention值）。

3.3 相关系数相乘

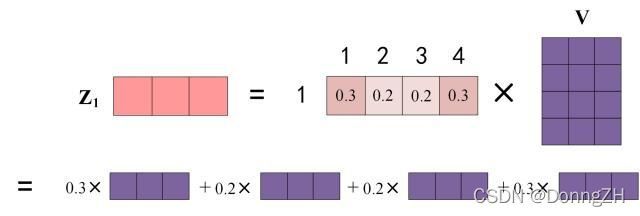
        图中 Softmax 矩阵的第 1 行表示单词 1 与其他所有单词的 attention 系数，最终单词 1 的输出等于所有单词的值根据 attention 系数相乘后加在一起得到，如下图所示：

3.4 self-attention的输出        

        得到 Softmax 矩阵之后可以和V相乘，得到最终的输出Z。

 4.self-attention的代码实现

from math import sqrt

import torch
import torch.nn as nn

class SelfAttention(nn.Module):
    def __init__(self, dim_q, dim_k, dim_v):
        super(SelfAttention, self).__init__()
        self.dim_q = dim_q
        self.dim_k = dim_k
        self.dim_v = dim_v

        #定义线性变换函数
        self.linear_q = nn.Linear(dim_q, dim_k, bias=False)
        self.linear_k = nn.Linear(dim_q, dim_k, bias=False)
        self.linear_v = nn.Linear(dim_q, dim_v, bias=False)
        self._norm_fact = 1 / sqrt(dim_k)

    def forward(self, x):
        # x: batch, n, dim_q
        #根据文本获得相应的维度

        batch, n, dim_q = x.shape
        assert dim_q == self.dim_q

        q = self.linear_q(x)  # batch, n, dim_k
        k = self.linear_k(x)  # batch, n, dim_k
        v = self.linear_v(x)  # batch, n, dim_v
        #q*k的转置 并*开根号后的dk
        dist = torch.bmm(q, k.transpose(1, 2)) * self._norm_fact  # batch, n, n
        #归一化获得attention的相关系数
        dist = torch.softmax(dist, dim=-1)  # batch, n, n
        #attention系数和v相乘，获得最终的得分
        att = torch.bmm(dist, v)
        return att

图reference:Transformer模型详解（图解最完整版） - 知乎 (zhihu.com)