神经网络与深度学习（七）循环神经网络（3）LSTM的记忆能力实验

---

使用LSTM模型重新进行数字求和实验，验证LSTM模型的长程依赖能力。

6.3 LSTM的记忆能力实验

  长短期记忆网络（Long Short-Term Memory Network，LSTM）是一种可以有效缓解长程依赖问题的循环神经网络．LSTM 的特点是引入了一个新的内部状态（Internal State）$c\in {\mathbb{R}}^D$ 和门控机制（Gating Mechanism）．不同时刻的内部状态以近似线性的方式进行传递，从而缓解梯度消失或梯度爆炸问题．同时门控机制进行信息筛选，可以有效地增加记忆能力．例如，输入门可以让网络忽略无关紧要的输入信息，遗忘门可以使得网络保留有用的历史信息．在上一节的数字求和任务中，如果模型能够记住前两个非零数字，同时忽略掉一些不重要的干扰信息，那么即时序列很长，模型也有效地进行预测.
  LSTM 模型在第 $t$ 步时，循环单元的内部结构如下图所示。

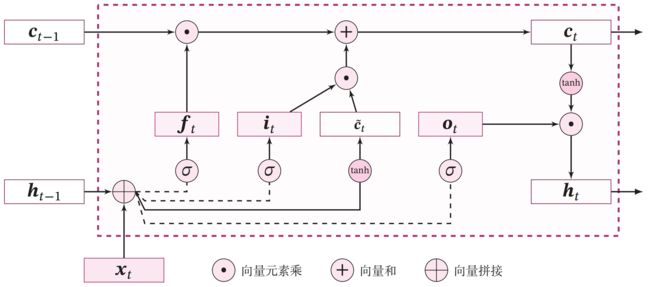
提醒：为了和代码的实现保存一致性，这里使用形状为 (样本数量 × 序列长度 × 特征维度) 的张量来表示一组样本.

  假设一组输入序列为$X\in {\mathbb{R}}^{B\times L\times M}$，其中$B$为批大小，$L$为序列长度，$M$为输入特征维度，LSTM从从左到右依次扫描序列，并通过循环单元计算更新每一时刻的状态内部状态$C_t\in {\mathbb{R}}^{B\times D}$和输出状态$H_t\in {\mathbb{R}}^{B\times D}$。

具体计算分为三步：

（1）计算三个“门”

 在时刻$t$，LSTM的循环单元将当前时刻的输入$X_t\in {\mathbb{R}}^{B\times M}$与上一时刻的输出状态$H_{t-1}\in {\mathbb{R}}^{B\times D}$，计算一组输入门$I_t$、遗忘门$F_t$和输出门$O_t$，其计算公式为
$$I_t=\sigma (X_t{W}_i+H_{t-1}{U}_i+b_i)\in {\mathbb{R}}^{B\times D},$$$$F_t=\sigma (X_t{W}_f+H_{t-1}{U}_f+b_f)\in {\mathbb{R}}^{B\times D},$$$$O_t=\sigma (X_t{W}_o+H_{t-1}{U}_o+b_o)\in {\mathbb{R}}^{B\times D},$$  其中$W_{\ast }\in {\mathbb{R}}^{M\times D},U_{\ast }\in {\mathbb{R}}^{D\times D},b_{\ast }\in {\mathbb{R}}^D$为可学习的参数，$\sigma$表示Logistic函数，将“门”的取值控制在$(0,1)$区间。这里的“门”都是$B$个样本组成的矩阵，每一行为一个样本的“门”向量。

（2）计算内部状态

 首先计算候选内部状态：$$C_t=tanh(X_t{W}_c+H_{t-1}{U}_c+b_c)\in {\mathbb{R}}^{B\times D},$$ 其中$W_c\in {\mathbb{R}}^{M\times D},U_c\in {\mathbb{R}}^{D\times D},b_c\in {\mathbb{R}}^D$为可学习的参数。

 使用遗忘门和输入门，计算时刻tt的内部状态：$$C_t=F_t\odot C_{t-1}+I_t\odot C_t,$$ 其中$\odot$为逐元素积。
3）计算输出状态
 当前LSTM单元状态（候选状态）的计算公式为:
 LSTM单元状态向量$C_t$和$H_t$的计算公式为:
$$C_t=F_t\odot C_{t-1}+I_t\odot C_t，$$$$H_t=O_t\odot tanh(C_t).$$ LSTM循环单元结构的输入是$t-1$时刻内部状态向量$C_{t-1}\in {\mathbb{R}}^{B\times D}$和隐状态向量$H_{t-1}\in {\mathbb{R}}^{B\times D}$，输出是当前时刻tt的状态向量$C_t\in {\mathbb{R}}^{B\times D}$和隐状态向量$H_t\in {\mathbb{R}}^{B\times D}$。通过LSTM循环单元，整个网络可以建立较长距离的时序依赖关系。
 通过学习这些门的设置，LSTM可以选择性地忽略或者强化当前的记忆或是输入信息，帮助网络更好地学习长句子的语义信息。
 在本节中，我们使用LSTM模型重新进行数字求和实验，验证LSTM模型的长程依赖能力。

6.3.1 模型构建

  在本实验中，我们将使用第6.1.2.4节中定义Model_RNN4SeqClass模型，并构建 LSTM 算子．只需要实例化 LSTM 算，并传入Model_RNN4SeqClass模型，就可以用 LSTM 进行数字求和实验。

6.3.1.1 LSTM层

  LSTM层的代码与SRN层结构相似，只是在SRN层的基础上增加了内部状态、输入门、遗忘门和输出门的定义和计算。这里LSTM层的输出也依然为序列的最后一个位置的隐状态向量。代码实现如下：

import torch
import torch.nn as nn
import torch.nn.functional as F
 
 
class LSTM(nn.Module):
    def __init__(self, input_size, hidden_size, Wi_attr=None, Wf_attr=None, Wo_attr=None, Wc_attr=None,
                 Ui_attr=None, Uf_attr=None, Uo_attr=None, Uc_attr=None, bi_attr=None, bf_attr=None,
                 bo_attr=None, bc_attr=None):
        super(LSTM, self).__init__()
        self.input_size = input_size
        self.hidden_size = hidden_size
        W_i = torch.randn([input_size, hidden_size])
        W_f = torch.randn([input_size, hidden_size])
        W_o = torch.randn([input_size, hidden_size])
        W_c = torch.randn([input_size, hidden_size])
        U_i = torch.randn([hidden_size, hidden_size])
        U_f = torch.randn([hidden_size, hidden_size])
        U_o = torch.randn([hidden_size, hidden_size])
        U_c = torch.randn([hidden_size, hidden_size])
        b_i = torch.randn([1, hidden_size])
        b_f = torch.randn([1, hidden_size])
        b_o = torch.randn([1, hidden_size])
        b_c = torch.randn([1, hidden_size])
        self.W_i = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(W_i, dtype=torch.float32), gain=1.0))
        # 初始化模型参数
        self.W_f = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(W_f, dtype=torch.float32), gain=1.0))
        self.W_o = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(W_o, dtype=torch.float32), gain=1.0))
        self.W_c = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(W_c, dtype=torch.float32), gain=1.0))
        self.U_i = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(U_i, dtype=torch.float32), gain=1.0))
        self.U_f = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(U_f, dtype=torch.float32), gain=1.0))
        self.U_o = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(U_o, dtype=torch.float32), gain=1.0))
        self.U_c = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(U_c, dtype=torch.float32), gain=1.0))
        self.b_i = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(b_i, dtype=torch.float32), gain=1.0))
        self.b_f = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(b_f, dtype=torch.float32), gain=1.0))
        self.b_o = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(b_o, dtype=torch.float32), gain=1.0))
        self.b_c = torch.nn.Parameter(torch.nn.init.xavier_uniform_(torch.as_tensor(b_c, dtype=torch.float32), gain=1.0))
 
    # 初始化状态向量和隐状态向量
    def init_state(self, batch_size):
        hidden_state = torch.zeros([batch_size, self.hidden_size])
        cell_state = torch.zeros([batch_size, self.hidden_size])
        return hidden_state, cell_state
 
    # 定义前向计算
    def forward(self, inputs, states=None):
        # inputs: 输入数据，其shape为batch_size x seq_len x input_size
        batch_size, seq_len, input_size = inputs.shape
 
        # 初始化起始的单元状态和隐状态向量，其shape为batch_size x hidden_size
        if states is None:
            states = self.init_state(batch_size)
        hidden_state, cell_state = states
 
        # 执行LSTM计算，包括：输入门、遗忘门和输出门、候选内部状态、内部状态和隐状态向量
        for step in range(seq_len):
            # 获取当前时刻的输入数据step_input: 其shape为batch_size x input_size
            step_input = inputs[:, step, :]
            # 计算输入门, 遗忘门和输出门, 其shape为：batch_size x hidden_size
            I_gate = F.sigmoid(torch.matmul(step_input, self.W_i) + torch.matmul(hidden_state, self.U_i) + self.b_i)
            F_gate = F.sigmoid(torch.matmul(step_input, self.W_f) + torch.matmul(hidden_state, self.U_f) + self.b_f)
            O_gate = F.sigmoid(torch.matmul(step_input, self.W_o) + torch.matmul(hidden_state, self.U_o) + self.b_o)
            # 计算候选状态向量, 其shape为：batch_size x hidden_size
            C_tilde = F.tanh(torch.matmul(step_input, self.W_c) + torch.matmul(hidden_state, self.U_c) + self.b_c)
            # 计算单元状态向量, 其shape为：batch_size x hidden_size
            cell_state = F_gate * cell_state + I_gate * C_tilde
            # 计算隐状态向量，其shape为：batch_size x hidden_size
            hidden_state = O_gate * F.tanh(cell_state)
 
        return hidden_state
    
    
Wi_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.2], [0.1, 0.2]]))
Wf_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.2], [0.1, 0.2]]))
Wo_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.2], [0.1, 0.2]]))
Wc_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.2], [0.1, 0.2]]))
Ui_attr = torch.nn.Parameter(torch.tensor([[0.0, 0.1], [0.1, 0.0]]))
Uf_attr = torch.nn.Parameter(torch.tensor([[0.0, 0.1], [0.1, 0.0]]))
Uo_attr = torch.nn.Parameter(torch.tensor([[0.0, 0.1], [0.1, 0.0]]))
Uc_attr = torch.nn.Parameter(torch.tensor([[0.0, 0.1], [0.1, 0.0]]))
bi_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.1]]))
bf_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.1]]))
bo_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.1]]))
bc_attr = torch.nn.Parameter(torch.tensor([[0.1, 0.1]]))
 
lstm = LSTM(2, 2, Wi_attr=Wi_attr, Wf_attr=Wf_attr, Wo_attr=Wo_attr, Wc_attr=Wc_attr,
                 Ui_attr=Ui_attr, Uf_attr=Uf_attr, Uo_attr=Uo_attr, Uc_attr=Uc_attr,
                 bi_attr=bi_attr, bf_attr=bf_attr, bo_attr=bo_attr, bc_attr=bc_attr)
 
inputs = torch.tensor([[[1, 0]]], dtype=torch.float32)
hidden_state = lstm(inputs)
print(hidden_state)

 运行结果如下：

  在飞桨框架已经内置了LSTM的API paddle.nn.LSTM，其与自己实现的SRN不同点在于其实现时采用了两个偏置，同时矩阵相乘时参数在输入数据前面，如下公式所示：

  这里我们可以将自己实现的SRN和torch框架内置的SRN返回的结果进行打印展示，实现代码如下。

batch_size, seq_len, input_size = 8, 20, 32
inputs = torch.randn([batch_size, seq_len, input_size])
 
# 设置模型的hidden_size
hidden_size = 32
torch_lstm = nn.LSTM(input_size, hidden_size)
self_lstm = LSTM(input_size, hidden_size)
 
self_hidden_state = self_lstm(inputs)
torch_outputs, (torch_hidden_state, torch_cell_state) = torch_lstm(inputs)
 
print("self_lstm hidden_state: ", self_hidden_state.shape)
print("torch_lstm outpus:", torch_outputs.shape)
print("torch_lstm hidden_state:", torch_hidden_state.shape)
print("torch_lstm cell_state:", torch_cell_state.shape)

 运行结果如下：

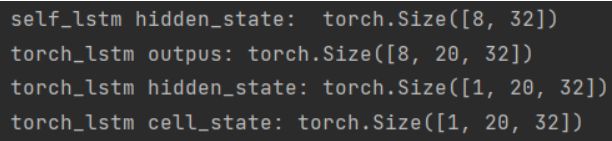
  在进行实验时，首先定义输入数据inputs，然后将该数据分别传入torch内置的LSTM与自己实现的LSTM模型中，最后通过对比两者的隐状态输出向量。代码实现如下：

import torch
torch.manual_seed(0)
 
# 这里创建一个随机数组作为测试数据，数据shape为batch_size x seq_len x input_size
batch_size, seq_len, input_size, hidden_size = 2, 5, 10, 10
inputs = torch.randn([batch_size, seq_len, input_size])
 
# 设置模型的hidden_size
# bih_attr = torch.nn.Parameter(torch.tensor(torch.zeros([4*hidden_size, ])))
torch_lstm = nn.LSTM(input_size, hidden_size, bias=True)
 
# 获取torch_lstm中的参数，并设置相应的paramAttr,用于初始化lstm
print(torch_lstm.weight_ih_l0.T.shape)
chunked_W = torch.split(torch_lstm.weight_ih_l0.T, 4, dim=-1)
chunked_U = torch.split(torch_lstm.weight_hh_l0.T, 4, dim=-1)
chunked_b = torch.split(torch_lstm.bias_hh_l0.T, 4, dim=-1)
 
Wi_attr = torch.nn.Parameter(torch.tensor(chunked_W[0].clone().detach().requires_grad_(True)))
Wf_attr = torch.nn.Parameter(torch.tensor(chunked_W[1].clone().detach().requires_grad_(True)))
Wc_attr = torch.nn.Parameter(torch.tensor(chunked_W[2].clone().detach().requires_grad_(True)))
Wo_attr = torch.nn.Parameter(torch.tensor(chunked_W[3].clone().detach().requires_grad_(True)))
Ui_attr = torch.nn.Parameter(torch.tensor(chunked_U[0].clone().detach().requires_grad_(True)))
Uf_attr = torch.nn.Parameter(torch.tensor(chunked_U[1].clone().detach().requires_grad_(True)))
Uc_attr = torch.nn.Parameter(torch.tensor(chunked_U[2].clone().detach().requires_grad_(True)))
Uo_attr = torch.nn.Parameter(torch.tensor(chunked_U[3].clone().detach().requires_grad_(True)))
bi_attr = torch.nn.Parameter(torch.tensor(chunked_b[0].clone().detach().requires_grad_(True)))
bf_attr = torch.nn.Parameter(torch.tensor(chunked_b[1].clone().detach().requires_grad_(True)))
bc_attr = torch.nn.Parameter(torch.tensor(chunked_b[2].clone().detach().requires_grad_(True)))
bo_attr = torch.nn.Parameter(torch.tensor(chunked_b[3].clone().detach().requires_grad_(True)))
self_lstm = LSTM(input_size, hidden_size, Wi_attr=Wi_attr, Wf_attr=Wf_attr, Wo_attr=Wo_attr, Wc_attr=Wc_attr,
                 Ui_attr=Ui_attr, Uf_attr=Uf_attr, Uo_attr=Uo_attr, Uc_attr=Uc_attr,
                 bi_attr=bi_attr, bf_attr=bf_attr, bo_attr=bo_attr, bc_attr=bc_attr)
 
# 进行前向计算，获取隐状态向量，并打印展示
self_hidden_state = self_lstm(inputs)
torch_outputs, (torch_hidden_state, _) = torch_lstm(inputs)
print("torch SRN:\n", torch_hidden_state.detach().numpy().squeeze(0))
print("self SRN:\n", self_hidden_state.detach().numpy())

 运行结果如下：

torch.Size([10, 40])
torch SRN:
 [[ 0.05112648  0.0069804  -0.03931074  0.08884123  0.1154766  -0.13408035
   0.16033086  0.00135597 -0.063761   -0.2974773 ]
 [ 0.11241535  0.07274596  0.36305282 -0.06277131  0.01287347 -0.15761302
   0.22385652  0.01972566 -0.35233897 -0.20609131]
 [ 0.13069034 -0.03020173 -0.06369952  0.13535677  0.34181935 -0.11440603
   0.10832833  0.04234035  0.08991402 -0.15160468]
 [ 0.0727646   0.15715013  0.06807105  0.07414021  0.3629469  -0.06236503
  -0.11784356  0.00420525 -0.1500205   0.08434851]
 [ 0.07962178  0.01809997 -0.02799227 -0.0978313  -0.08596172 -0.13848482
   0.06129254  0.15295173 -0.14451738 -0.11927365]]
self SRN:
 [[ 0.25522318 -0.26233613  0.579096    0.21594535 -0.04982951 -0.2876913
   0.04644723 -0.10902733  0.10669092  0.4416803 ]
 [ 0.1569139  -0.07310869 -0.01197558  0.04463004 -0.15551823 -0.04395698
   0.08646112 -0.24415644 -0.34958637  0.22522162]]

  可以看到，两者的输出基本是一致的。另外，还可以进行对比两者在运算速度方面的差异。代码实现如下：

import time
 
# 这里创建一个随机数组作为测试数据，数据shape为batch_size x seq_len x input_size
batch_size, seq_len, input_size = 8, 20, 32
inputs = torch.randn([batch_size, seq_len, input_size])
 
# 设置模型的hidden_size
hidden_size = 32
self_lstm = LSTM(input_size, hidden_size)
torch_lstm = nn.LSTM(input_size, hidden_size)
 
# 计算自己实现的SRN运算速度
model_time = 0
for i in range(100):
    strat_time = time.time()
    hidden_state = self_lstm(inputs)
    # 预热10次运算，不计入最终速度统计
    if i < 10:
        continue
    end_time = time.time()
    model_time += (end_time - strat_time)
avg_model_time = model_time / 90
print('self_lstm speed:', avg_model_time, 's')
 
# 计算torch内置的SRN运算速度
model_time = 0
for i in range(100):
    strat_time = time.time()
    outputs, (hidden_state, cell_state) = torch_lstm(inputs)
    # 预热10次运算，不计入最终速度统计
    if i < 10:
        continue
    end_time = time.time()
    model_time += (end_time - strat_time)
avg_model_time = model_time / 90
print('torch_lstm speed:', avg_model_time, 's')

 运行结果如下：

 可以看到，torch框架内置的LSTM运行效率远远高于自己实现的LSTM。

6.3.1.2 模型汇总

  在本节实验中，我们将使用6.1.2.4的Model_RNN4SeqClass作为预测模型，不同在于在实例化时将传入实例化的LSTM层。

6.3.2 模型训练

6.3.2.1 训练指定长度的数字预测模型

  本节将基于RunnerV3类进行训练，首先定义模型训练的超参数，并保证和简单循环网络的超参数一致. 然后定义一个train函数，其可以通过指定长度的数据集，并进行训练. 在train函数中，首先加载长度为length的数据，然后实例化各项组件并创建对应的Runner，然后训练该Runner。同时在本节将使用4.5.4节定义的准确度（Accuracy）作为评估指标，代码实现如下：

# 基于RNN实现数字预测的模型
class Model_RNN4SeqClass(nn.Module):
    def __init__(self, model, num_digits, input_size, hidden_size, num_classes):
        super(Model_RNN4SeqClass, self).__init__()
        # 传入实例化的RNN层，例如SRN
        self.rnn_model = model
        # 词典大小
        self.num_digits = num_digits
        # 嵌入向量的维度
        self.input_size = input_size
        # 定义Embedding层
        self.embedding = Embedding(num_digits, input_size)
        # 定义线性层
        self.linear = nn.Linear(hidden_size, num_classes)
 
    def forward(self, inputs):
        # 将数字序列映射为相应向量
        inputs_emb = self.embedding(inputs)
        # 调用RNN模型
        hidden_state = self.rnn_model(inputs_emb)
        # 使用最后一个时刻的状态进行数字预测
        logits = self.linear(hidden_state)
        return logits

6.3.2.2 多组训练

  接下来，分别进行数据长度为10, 15, 20, 25, 30, 35的数字预测模型训练实验，训练后的runner保存至runners字典中。

# LSTM训练
lstm_runners = {}
lengths = [10, 15, 20, 25, 30, 35]
for length in lengths:
    runner = train(length)
    lstm_runners[length] = runner

 运行结果如下：

6.3.2.3 损失曲线展示

  分别画出基于LSTM的各个长度的数字预测模型训练过程中，在训练集和验证集上的损失曲线，代码实现如下：

# # 画出训练过程中的损失图
for length in lengths:
    runner = lstm_runners[length]
    fig_name = f"D:/datasets/images/6.11_{length}.pdf"
    plot_training_loss(runner, fig_name, sample_step=100)

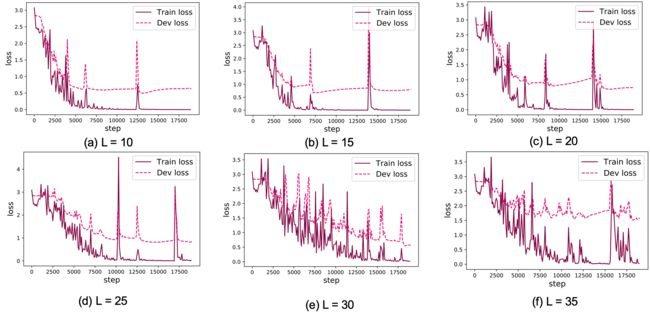
  下图展示了LSTM模型在不同长度数据集上进行训练后的损失变化，同SRN模型一样，随着序列长度的增加，训练集上的损失逐渐不稳定，验证集上的损失整体趋向于变大，这说明当序列长度增加时，保持长期依赖的能力同样在逐渐变弱. 同图6.5相比，LSTM模型在序列长度增加时，收敛情况比SRN模型更好。

6.3.3 模型评价

6.3.3.1 在测试集上进行模型评价

  使用测试数据对在训练过程中保存的最好模型进行评价，观察模型在测试集上的准确率. 同时获取模型在训练过程中在验证集上最好的准确率，实现代码如下:

#lstm
lstm_dev_scores = []
lstm_test_scores = []
for length in lengths:
    print(f"Evaluate LSTM with data length {length}.")
    runner = lstm_runners[length]
    # 加载训练过程中效果最好的模型
    model_path = os.path.join(save_dir, f"best_lstm_model_{length}.pdparams")
    runner.load_model(model_path)
 
    # 加载长度为length的数据
    data_path = f"D:/datasets/{length}"
    train_examples, dev_examples, test_examples = load_data(data_path)
    test_set = DigitSumDataset(test_examples)
    test_loader = DataLoader(test_set, batch_size=batch_size)
 
    # 使用测试集评价模型，获取测试集上的预测准确率
    score, _ = runner.evaluate(test_loader)
    lstm_test_scores.append(score)
    lstm_dev_scores.append(max(runner.dev_scores))
 
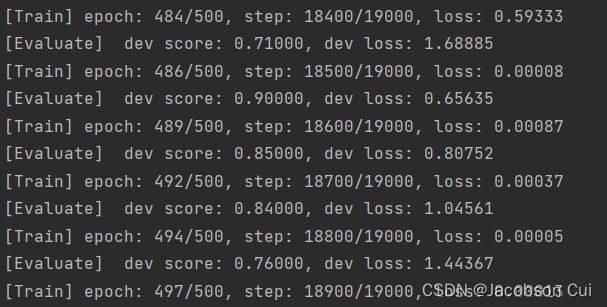
for length, dev_score, test_score in zip(lengths, lstm_dev_scores, lstm_test_scores):
    print(f"[LSTM] length:{length}, dev_score: {dev_score}, test_score: {test_score: .5f}")
 
#训练SRN模型
srn_runners = {}
lengths = [10, 15, 20, 25, 30, 35]
for length in lengths:
    runner = train(length)
    srn_runners[length] = runner
srn_dev_scores = []
srn_test_scores = []
for length in lengths:
    print(f"Evaluate SRN with data length {length}.")
    runner = srn_runners[length]
    # 加载训练过程中效果最好的模型
    model_path = os.path.join(save_dir, f"best_srn_model_{length}.pdparams")
    runner.load_model(model_path)
 
    # 加载长度为length的数据
    data_path = f"D:/datasets/{length}"
    train_examples, dev_examples, test_examples = load_data(data_path)
    test_set = DigitSumDataset(test_examples)
    test_loader = torch.utils.data.DataLoader(test_set, batch_size=batch_size)
 
    # 使用测试集评价模型，获取测试集上的预测准确率
    score, _ = runner.evaluate(test_loader)
    srn_test_scores.append(score)
    srn_dev_scores.append(max(runner.dev_scores))
 
for length, dev_score, test_score in zip(lengths, srn_dev_scores, srn_test_scores):
    print(f"[SRN] length:{length}, dev_score: {dev_score}, test_score: {test_score: .5f}")
 

6.3.3.2 模型在不同长度的数据集上的准确率变化图

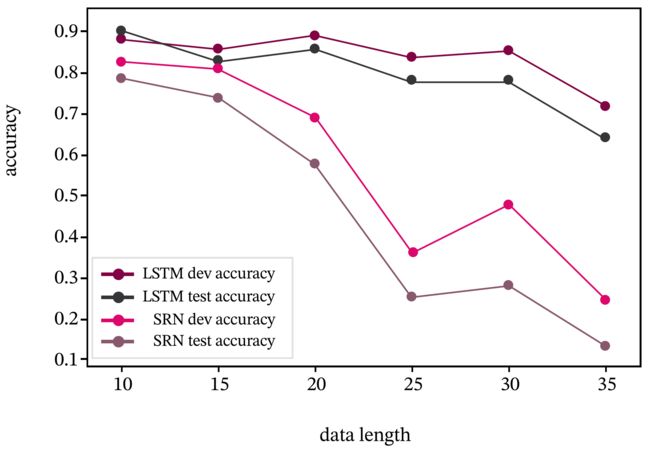
  接下来，将SRN和LSTM在不同长度的验证集和测试集数据上的准确率绘制成图片，以方面观察。

#绘制全部图
import matplotlib.pyplot as plt
 
plt.plot(lengths, lstm_dev_scores, '-o', color='#e8609b',  label="LSTM Dev Accuracy")
plt.plot(lengths, lstm_test_scores,'-o', color='#000000', label="LSTM Test Accuracy")
 
#绘制坐标轴和图例
plt.ylabel("accuracy", fontsize='large')
plt.xlabel("sequence length", fontsize='large')
plt.legend(loc='lower left', fontsize='x-large')
 
fig_name = "D:/datasets/images/6.12.pdf"
plt.savefig(fig_name)
plt.show()

  下图展示了LSTM模型与SRN模型在不同长度数据集上的准确度对比。随着数据集长度的增加，LSTM模型在验证集和测试集上的准确率整体也趋向于降低；同时LSTM模型的准确率显著高于SRN模型，表明LSTM模型保持长期依赖的能力要优于SRN模型.

6.3.3.3 LSTM模型门状态和单元状态的变化

  LSTM模型通过门控机制控制信息的单元状态的更新，这里可以观察当LSTM在处理一条数字序列的时候，相应门和单元状态是如何变化的。首先需要对以上LSTM模型实现代码中，定义相应列表进行存储这些门和单元状态在每个时刻的向量。

import torch.nn.functional as F
 
 
 
# 实例化模型
model = LSTM(input_size, hidden_size)
model = Model_RNN4SeqClass(model, num_digits, input_size, hidden_size, num_classes)
# 指定优化器
lr = 0.001
optimizer = torch.optim.Adam(model.parameters(),lr)
# 定义评价指标
metric = Accuracy()
# 定义损失函数
loss_fn = torch.nn.CrossEntropyLoss()
# 基于以上组件，重新实例化Runner
runner = RunnerV3(model, optimizer, loss_fn, metric)
 
length = 10
# 加载训练过程中效果最好的模型
model_path = os.path.join(save_dir, f"best_lstm_model_{length}.pdparams")
runner.load_model(model_path)
 
import seaborn as sns
 
def plot_tensor(inputs, tensor,  save_path, vmin=0, vmax=1):
    import matplotlib.pyplot as plt
    tensor = np.stack(tensor, axis=0)
    tensor = np.squeeze(tensor, 1).T
 
    plt.figure(figsize=(16,6))
    # vmin, vmax定义了色彩图的上下界
    ax = sns.heatmap(tensor, vmin=vmin, vmax=vmax)
    ax.set_xticklabels(inputs)
    ax.figure.savefig(save_path)
 
 
# 定义模型输入
inputs = [6, 7, 0, 0, 1, 0, 0, 0, 0, 0]
X = torch.tensor(inputs.copy())
X = X.unsqueeze(0)
# 进行模型预测，并获取相应的预测结果
logits = runner.predict(X)
predict_label = torch.argmax(logits, dim=-1)
print(f"predict result: {predict_label.numpy()[0]}")
# 输入门
Is= runner.model.rnn_model.Is
plot_tensor(inputs, Is, save_path="D:/datasets/images/6.13_I.pdf")
# 遗忘门
Fs = runner.model.rnn_model.Fs
plot_tensor(inputs, Fs, save_path="D:/datasets/images/6.13_F.pdf")
# 输出门
Os = runner.model.rnn_model.Os
plot_tensor(inputs, Os, save_path="D:/datasets/images/6.13_O.pdf")
# 单元状态
Cs = runner.model.rnn_model.Cs
plot_tensor(inputs, Cs, save_path="D:/datasets/images/6.13_C.pdf", vmin=-5, vmax=5)

 运行结果如图：

  上图中横坐标为输入数字，纵坐标为相应门或单元状态向量的维度，颜色的深浅代表数值的大小。
  输入门我们可以看到当输入不同的数字时，我们保持了输入相对一致的大小。
  遗忘门我们可以看到，相对于输入，一部分维度开始变浅，说明我们对这部分维度进行了遗忘。
  输出门和单元状态我们可以看到在某些维度上数值变小，某些维度上数值变大，表明输出门对于某些信息进行保留，对于某些信息进行遗忘，从而得到了该种形式的输出。

【思考题2】LSTM与SRN在不同长度数据集上的准确度对比，谈谈看法。

  通过实验结果我们可以发现,SRN在长度为20左右的时候出现了问题，准确率大幅度下降。而LSTM准确率依旧维持在一个稳定的范围内，所以说LSTM比SRN更聪明一点，能够记住自己想要的东西。

【思考题3】分析LSTM中单元状态和门数值的变化图，并用自己的话解释该图。

  色阶图中，颜色的深浅代表着数值的大小，，输入门大小为0时，颜色差不多相近大小近似一致，表明对于0元素进行过滤，过滤掉不需要的信息，遗忘门为1的地方，数值变小，表示对不需要的信息进行遗忘，随着序列的输入，输出门和单元状态在某些维度上数值变小，在某些维度上数值变大，表示输出们对输出的信息进行选择，输出重要的信息。

全面总结RNN

参考

https://blog.csdn.net/weixin_53651790/article/details/128091975?spm=1001.2014.3001.5502
NNDL 实验6（上）
https://blog.csdn.net/qq_38975453/article/details/126800091?spm=1001.2014.3001.5502