matlab数学建模-神经网络感知器函数
感知器学习规则为调整权重和偏值,使得平局误差性能最小。
绘制样本点函数
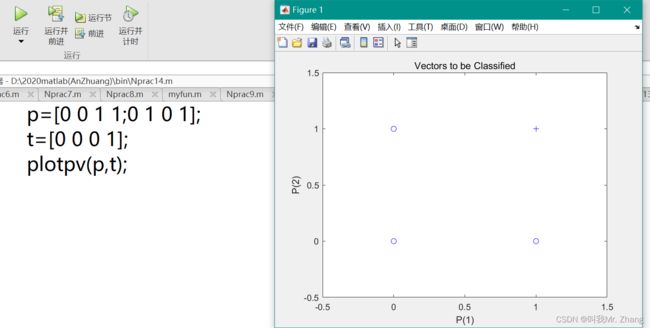
p=[0 0 1 1;0 1 0 1];
t=[0 0 0 1];
plotpv(p,t);绘制分类线函数
plotp(W,B);
W是权重 B是向量感知器学习函数
[dW,dS]=learnp(P,T,E)
dW,dS 分别是误差权值变换矩阵
P输入向量 T目标向量 E误差向量平均绝对误差性能函数mae
clear all
clc
net=perceptron;
net=configure(net,0,0);
p=[-10 -5 0 5 10];
t=[0 0 1 1 1];
y=net(p);
e=t-y;
perf=mae(e)误差平方和性能函数
clear all
clc
%系统自带的一个矩阵
[x,t]=simplefit_dataset;
net=fitnet(10);
%fitnet 拟合神经网络
net.performFcn='sse';
net=train(net,x,t);
y=net(x);
perf=sse(net,t,y);
最大稳定学习速率函数
P=[1 2 -12 3;3 7 2 8];
lr=maxlinlr(P,'bias');网络学习函数
线性神经网络设计函数
clear all
clc
P={38 7 2 3 2 9};
Pi={2 3};
T={3 3.2 8 9 29 89};
net=newlind(P,T,Pi);
Y=sim(net,P,Pi);
均方误差性能函数
%BP神经网络函数
[x,t]=simplefit_dataset;
net=feedforwardnet(10);
net.performFcn='mse';
net.performParam.regularization=0.01;
net=train(net,x,t);
y=net(x);
perf=perform(net,t,y);
perf=mse(net,x,t,'regularization',0.01);
绘制误差曲面图函数
p=[-2 -3 -34];
t=[1 2 4];
wv=-4:0.4:4;
bv=wv;
ES=errsurf(p,t,wv,bv,'logsig');
plotes(wv,bv,ES,[60 30]);
%误差曲面绘制权值和偏值的位置
W=-3;
B=1;
E=sumsqr(t-sumuff(p,W,B,'logsig'));
plotep(W,B,e);
计算向量之间距离函数
%dist计算 矩阵和输入向量之间的距离
W=rand(4,3);
P=rand(3,1);
Z=dist(WzP);
径向基传递函数
%dist计算 矩阵和输入向量之间的距离
W=rand(4,3);
P=rand(3,1);
Z=dist(WzP);
建立径向神经网络函数newrb
clear all
clc
%输入
X=0:0.1:2;
%目标值
T=cos(X*pi);
%%画出采样点
figure(1);
plot(X,T,'+');
title('待逼近的函数采样点');
xlabel('输入值');
ylabel('目标值');
%%建立网络
n=-4:0.1:4;
a1=radbas(n);
a2=radbas(n-1.5);
a3=radbas(n+2);
a=a1+1*a2+1.5*a3;
figure(2);
plot(n,a1,n,a2,n,a3,n,a,'x');
title('径向函数加权和');
xlabel('输入');
ylabel('输出');
%仿真
net=newrb(X,T,1,2);
X1=0:0.01:2;
y=sim(net,X1);
figure(3);
plot(X1,y,X,T,'+');
title('仿真结果');
xlabel('输入');
ylabel('网络输出及目标输出');