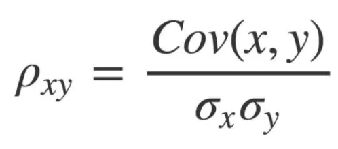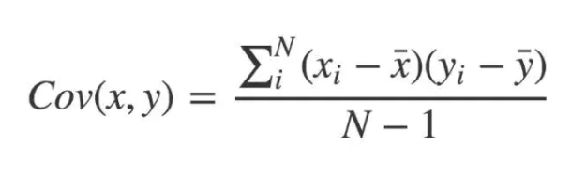大数据基础与应用课程作业2：数据探索

一、作业题目

22题至35题，其中27题不用做。

作业使用数据集是adult数据集，链接：
adult数据集
密码：6666

二、题目解答

1.观察数据

第22题：观察数据，查看哪些特征是分类变量，哪些是连续的数字变量。

（1）实验代码

# 读取数据
adult<-read.csv("datasets/Clem3Training",stringsAsFactors=TRUE)
# 查看数据概况
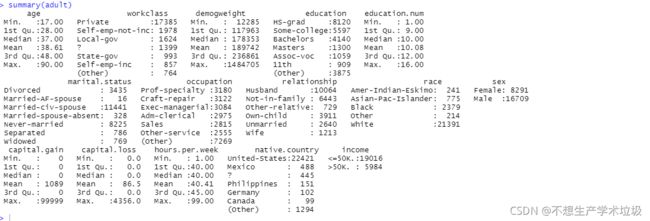
summary(adult)

（2）原理介绍

无

（3）实验结果

下图是summary()函数的结果：

（4）结果解释

由上面截图可以看到，分类变量有：
workclass，education，marital.status，occupation，relationship，race，sex，native.country，income
连续的数值变量有：
age，demogweight，education.num，capital.gain，capital.loss，hours.per.week

2.查看数据前十行

第23题：对数据集的前十个记录构建一个表，对数据进行体会

（1）实验代码

table_new<-head(adult,10)

（2）原理介绍

无

（3）实验结果

新建的表table_new的数据如下图所示：

（4）结果解释

初步观察数据，该数据集包含十五个特征，分别是：
这些特征可以参考一下这篇博客：
zure机器学习入门（三）创建Azure机器学习实验

特征名称	特征意义
age	年龄
workclass	工作类型，应该指为谁工作，如State-gov为州政府工作，Private为个人工作，Self-emp-not-inc为无限责任公司，或者理解为工作性质
demogweight	统计学权重，应该还有个名字叫Fnlwgt，表示在一个州内，dataset的一个观测代表的人数。
education	受教育程度
education.num	受教育年限
marital.status	婚育状况，已婚、未婚、离异什么的
occupation	职业，Adm-clerical行政文员
relationship	在家庭中的关系，如husband
race	种族，如白人white
sex	性别
capital.gain	资本盈利，估计是投资收入
capital.loss	资本损失，估计是投资赔的钱
hours.per.week	每周工作时间
native.county	国籍，如Cuba古巴
income	年收入

3.调查具有相关性的变量

第24题，要调查里面的变量是否具有相关性。
对观察变量的相关性计算只涉及连续变量，因此分类变量不参与相关性计算

（1）实验代码

# 计算相关系数
cor(cbind(adult$age,adult$demogweight, adult$education.num,adult$capital.gain,adult$capital.loss,hours.per.week))

（2）原理介绍

相关系数的计算：

其中协方差的计算公式为：

（3）实验结果

程序计算得到的相关系数矩阵如下图所示：

（4）结果解释

由上面的相关系数矩阵可以看到，这些数值变量之间的相关系数都很低，大多数都不超过0.1，只有受教育时长和投资盈利，受教育时常和每周工作时间有较弱的相关性，但仅为0.12-0.15左右，因此可以认为各数值变量之间不具有相关性。

4.对分类变量构建条形图

第25题：要求对每一个分类变量，都构建条形图，这个条形图中要体现出目标变量的堆叠，也即比例，如果必要的话可以进行规范化。回答下面的问题：

1. 讨论每个分类变量与目标变量的关系。
2. 你认为哪个分类变量会在之后的分类模型中做出巨大的贡献？

（1）实验代码

这里只给出income和workclass的代码，其他类似

# income 和 workclass的条形图
    # 绝对值条形图
income_workclass=table(adult$income,adult$workclass)
barplot(income_workclass)
    # 添加图例
legend("topright",c("<=50K", ">50K"),
               col = c("black","gray"),pch=15)
# 归一化后的条形图
income_workclass_ratio=round(prop.table(income_workclass,margin=2),4)*100
barplot(income_workclass_ratio)
    #  添加图例
legend("top",c("<=50K", ">50K"),
       col = c("black","gray"),pch=15)

（2）原理介绍

无

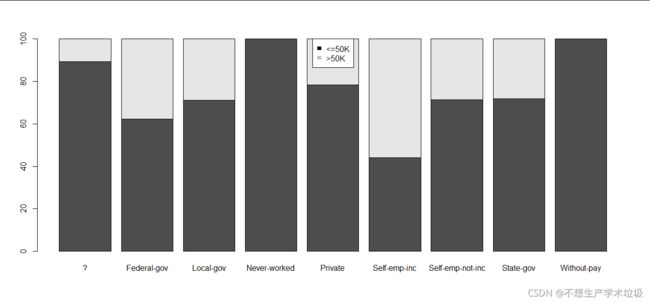
（3）实验结果

(a)income和workclass的条形图：

(b)income和education的条形图：

(c)income和marital.status的条形图：

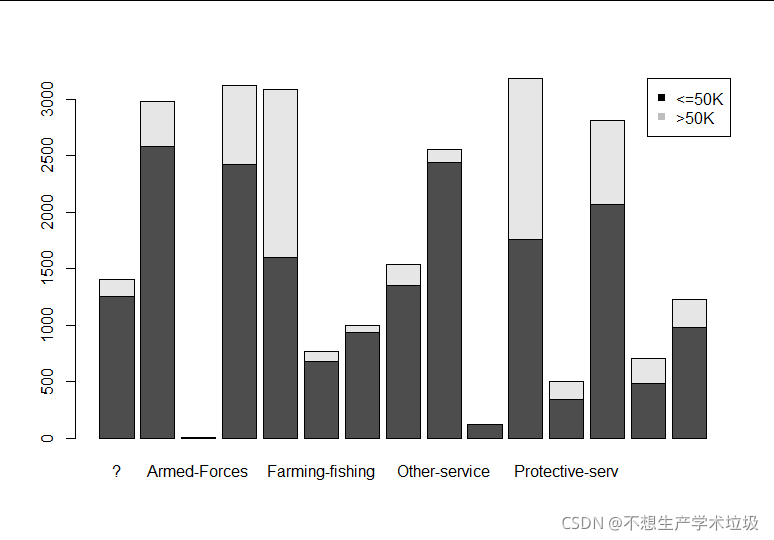
(d)income和occupation的条形图：

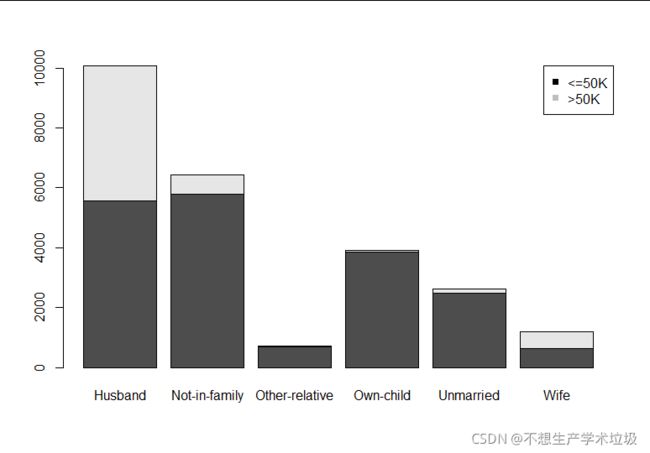
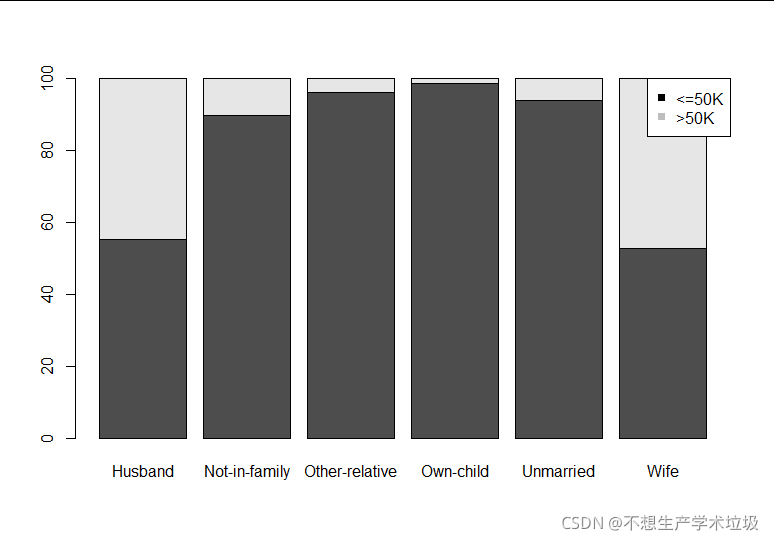
(e)income和relationship的条形图：


(f)income和race的条形图：

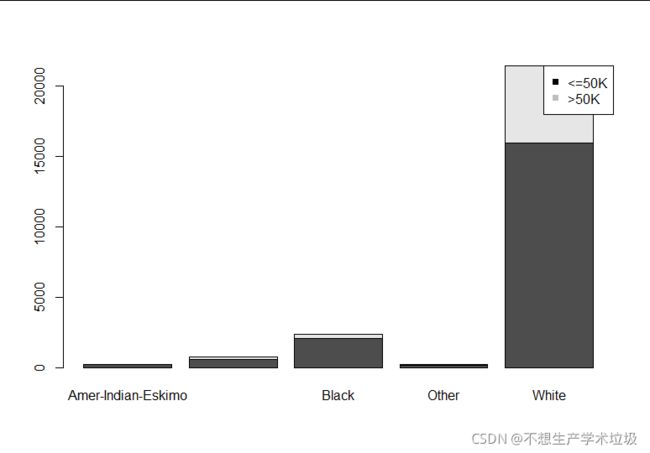
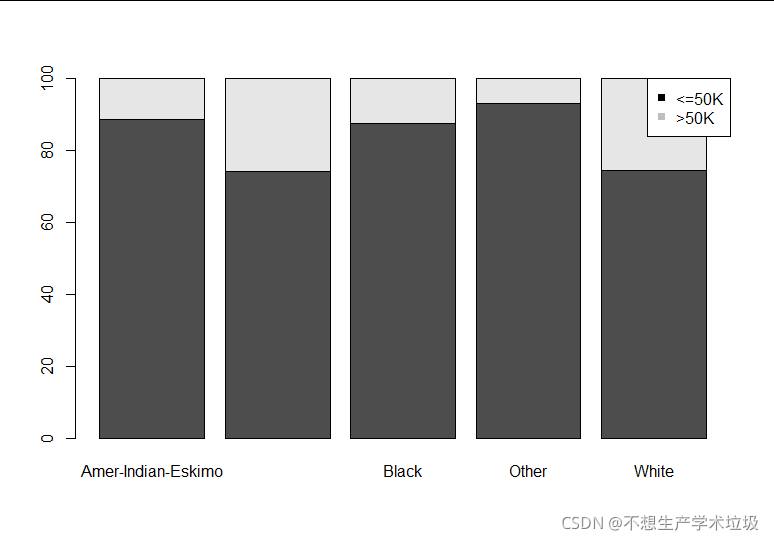
(g)income和sex的条形图：

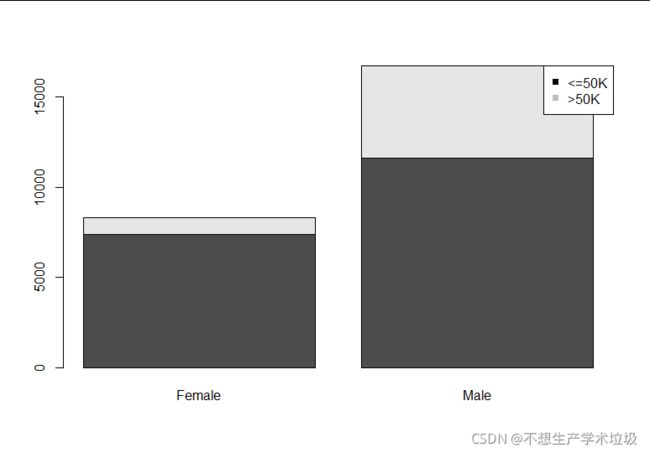
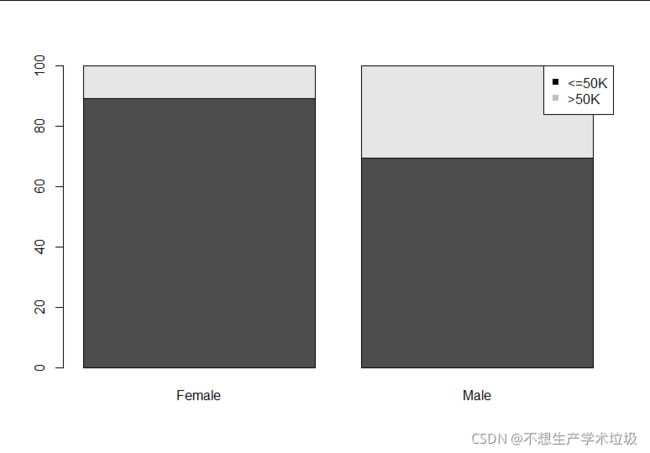
(h)income和native.country的条形图：

（4）结果解释

(a)income和workclass
不同的工作性质，导致收入的两个取值在不同的工作性质中有不同的比例。干义工的人收入都在50k以下

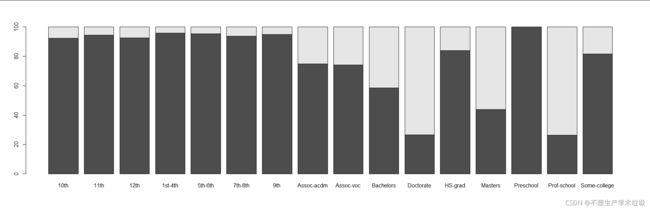
(b)income和education
在受教育水平较低的时候，两个目标变量的取值比例差不太多，但随着受教育水平的增高，一方面高收入的比例变大，另一方面在高教育经历中，其目标变量的比例会剧烈变化。

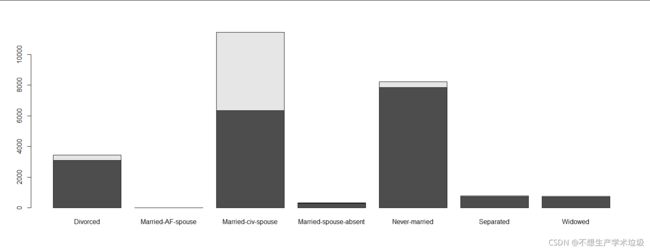
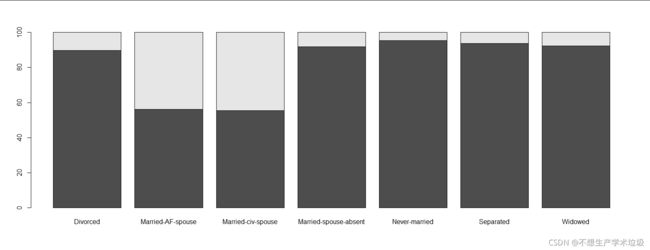
(c)income和marital.status
可以看到在家庭美满的情况下，高收入比例要远高于其他群体，可以推测家庭幸福美满有助于提高收入水平。

(d)income和occupation
不同职位，不同收入的比例不同，这可以理解。

(e)income和relationship
可以从结果看到，还没有孩子的husband和wife高收入的比例很高，说明他们没有养育孩子的情况下会更加投入到事业中。

(f)income和race
不同人种各种收入比例有一点不太均衡，但是差距在可允许的范围内。

(g)income和sex
男性高收入的比例明显大于女性。

(h)income和native.country
来自不同国家的人高低收入比例不同，这或许和经商的头脑以及文化有关。

经过以上分析，在分类变量中，除了race变量，其他变量都将会在后面的分类模型中做出巨大的贡献。

5.观察分类变量之间的关系

第26题：对每一对分类变量，构建一个交叉表，讨论其中非常显著的结论。

（1）实验代码

以workclass和education为例，其他类似：

# 绝对值
workclass_education=table(adult$workclass,adult$education)
workclass_education

（2）原理介绍

无

（3）实验结果

(a) workclass和education
(b) workclass和marital.status

(c) workclass和occupation

(d) workclass和relationship
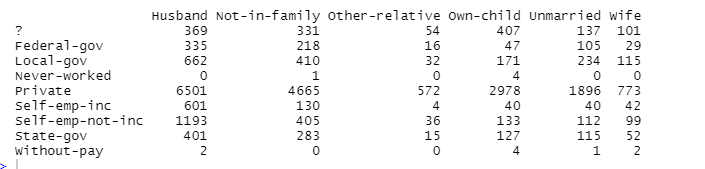(e) workclass和race
(f) workclass和sex

（4）结果解释

(a) workclass和education
从事不同workclass的人受教育水平不同

(b) workclass和marital.status
从事不同workclass的人的婚育情况分布差不多，例外在于“withou-pay”的人们，以从未结婚的人居多。

(c) workclass和occupation
大多数workclass场景下都有各种各样的occupation

(d) workclass和relationship
从事不同行业的人的家庭身份比例不同，

(e) workclass和race
可以看到不同行业中，白人所占的比例是最多的。

(f) workclass和sex
所列的行业中，男性所占的比例很大。

6.检查异常值

第28题：检查数据集中的异常之处，我们应该如何处理他们？
在数据中，很明显的异常就是有很多缺失值，而缺失值的表现形式为“？”，而不会被R读取时认定为NA，因此要做的就是识别出“？”并将值替换为NA，对待NA值可以采用取均值、随机抽样等方法填补数据。

7.数值型数据的统计特征

第29题：对每个数值型数据计算mean, median, minimum, maximum, and standard deviation
使用summary()可以得到mean、median、minium、maximum，标准差可以用sd()函数计算。
前者前面有图，不再赘述。

（1）实验代码

# 得到均值等特征
summary(adult)
sd(adult$age)

（2）实验结果

实验结果：
标准差：
age:13.68777
demogweight:105294.7
education.num:2.557035
capital.gain:7486.621
capital.loss:401.2536
hours.per.week:12.29927

8.对数值型数据构建直方图

第30题：为每一个数值型变量构建一个直方图histogram，然后将目标变量在直方图上进行堆叠，如果有必要，就进行标准化。并回答如下问题：

1. 讨论每个数值型变量和目标变量的关系
2. 在之后的数据挖掘分类模型中，你认为哪个数值型变量将会对结果做出巨大贡献？

（1）实验代码

以income和age的关系为例：
由于age的范围一般为0-100，故以20为单位进行分桶，将连续的数值型变量转化成较少的离散值

adult$age_round=floor(adult$age/20)
head(adult$age_round,5)
ggplot() +
 geom_bar(data = adult,
          aes(x = factor(age_round),
              fill = factor(income)),
          position = "fill") +
 scale_x_discrete("年龄age") +
 scale_y_continuous("百分比") +
 guides(fill=guide_legend(title="income")) +
 scale_fill_manual(values=c("blue", "red"))

（2）原理介绍

无

（3）实验结果

(a)income在不同age段的分布


(b)income在不同demogweiht段的分布
demogweiht分布在12285 - 1484705 之间，故以10w为一个桶（横坐标懒得改了）

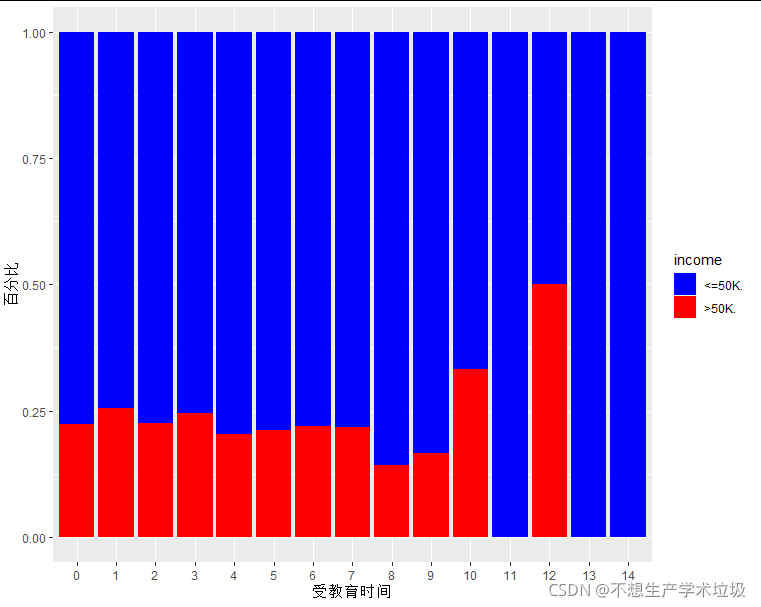
(c)income在不同education.num段的分布
以5年为一个桶：
(d)income在不同captal.gain段的分布
captal.gain在0-10k之间分布，故以1k为一个桶
（横坐标的名字忘了改了）

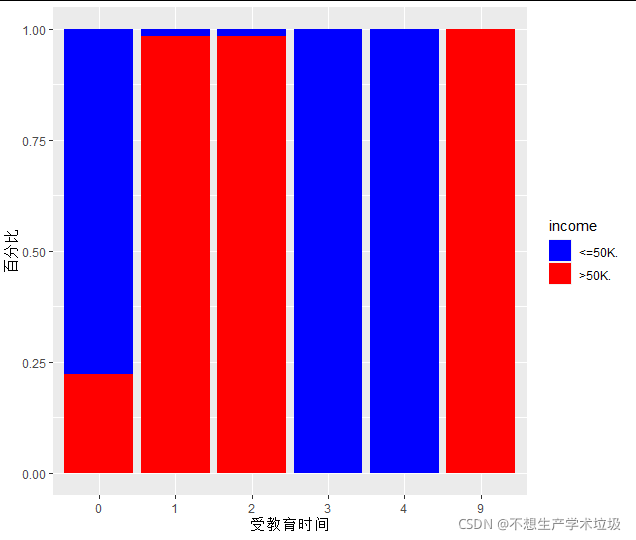
(e)income在不同captal.loss段的分布
loss分布在0-5000之间，以1000为一个桶
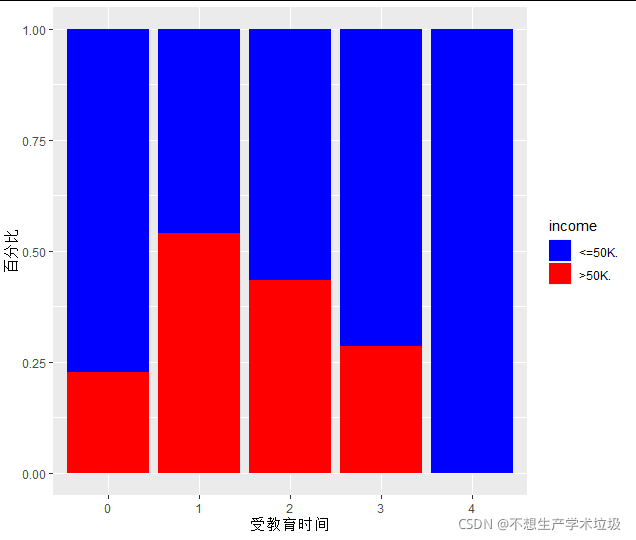(f)income在不同hours.per.week段的分布
hours.per.week范围是0-100，故以10为桶：

（4）结果解释：

(a)income在不同age段的分布
中年人的高收入比例更高

(b)income在不同demogweiht段的分布
无

(c)income在不同education.num段的分布
随着受教育时间的增长，高收入的比例明显增加

(d)income在不同captal.gain段的分布
income和投资盈利似乎没有必然的联系，高投资盈利似乎会导致更高的收入

(e)income在不同captal.loss段的分布
投资损失越大，一般收入越低。

(f)income在不同hours.per.week段的分布
大的工作时间一般比小的工作时间高收入的比例要高。

综上，在后面的分类模型中，很有可能对结果做出巨大贡献的数字型变量是：age，education.num，hours.per.week

9.探索数值型变量之间的关系

第31题：对每一对数值型变量，画出散点图，发现有什么显著之处？

（1）实验代码

以capital.gain和captital.loss为例的代码：

plot(adult$capital.gain,adult$capital.loss,
     xlim = c(0, 100000),
     ylim = c(0, 5000),
     xlab = "capital.gain",ylab = "capital.loss",
     col = ifelse(adult$income=="<=50K.","red","blue"))
legend("topright",c("<=50K", ">50K"),
       col = c("red","blue"),pch = 1,               #pch：数据点的形状
       title = "adult")

（2）原理介绍

无

（3）实验结果

由于demogweight没什么意义，故不研究它
(a)age和education.num散点图
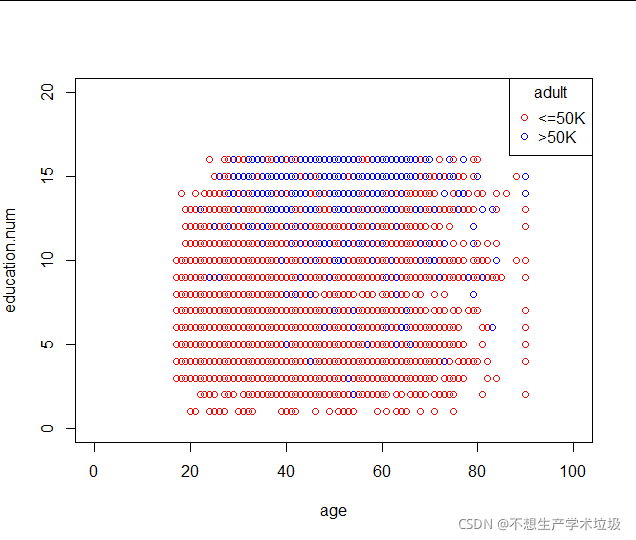(b)age和capital.gain散点图

(c)age和capital.loss散点图
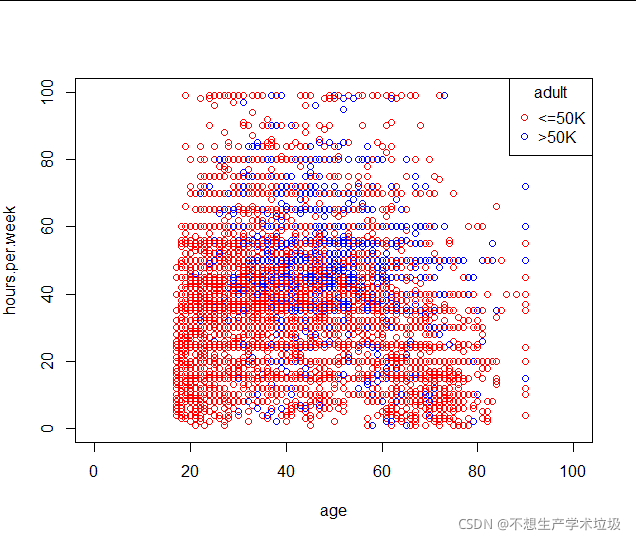
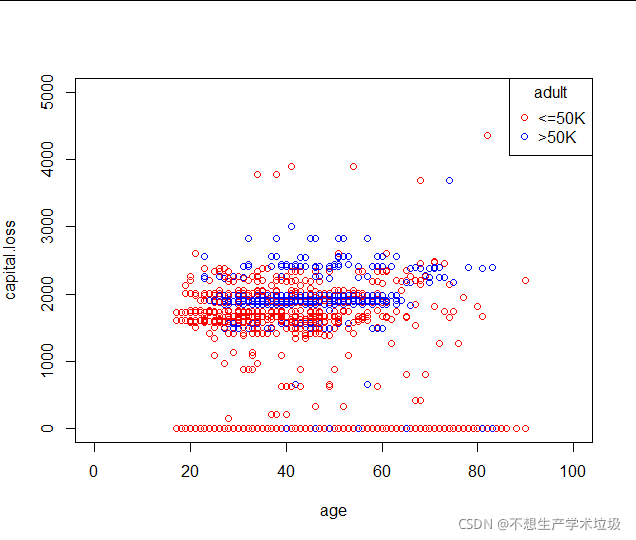(d)age和hours.per.week散点图

(e)education.num和capital.gain散点图

(f)education.num和capital.loss散点图
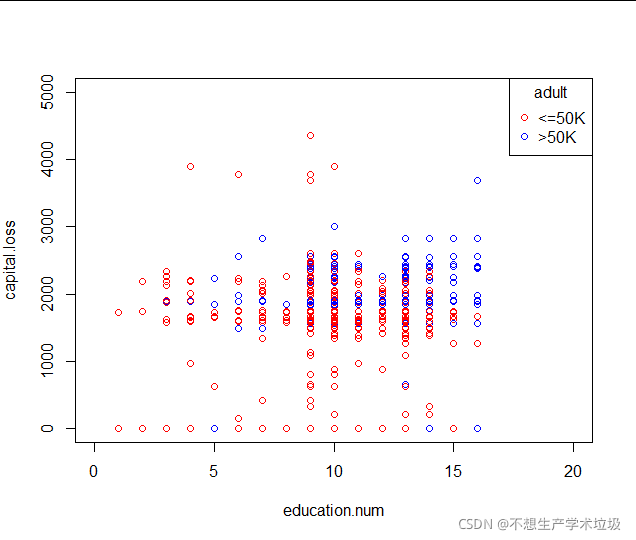(g)education.num和hours.per.week散点图

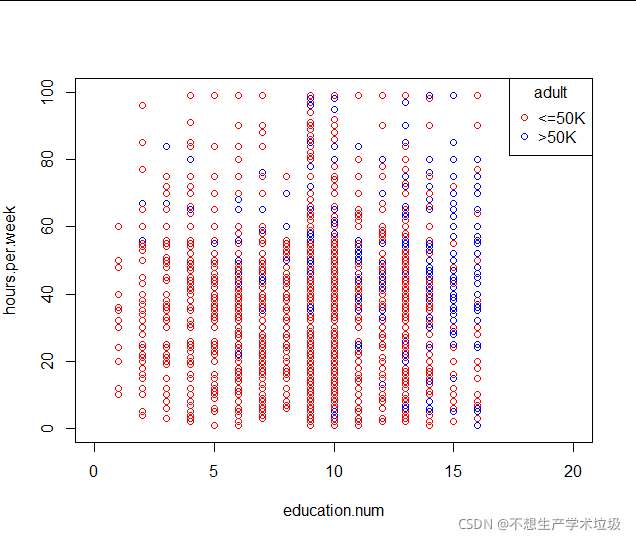
(h)capital.gain和captal.loss散点图

(i)capital.gain和hours.per.week散点图

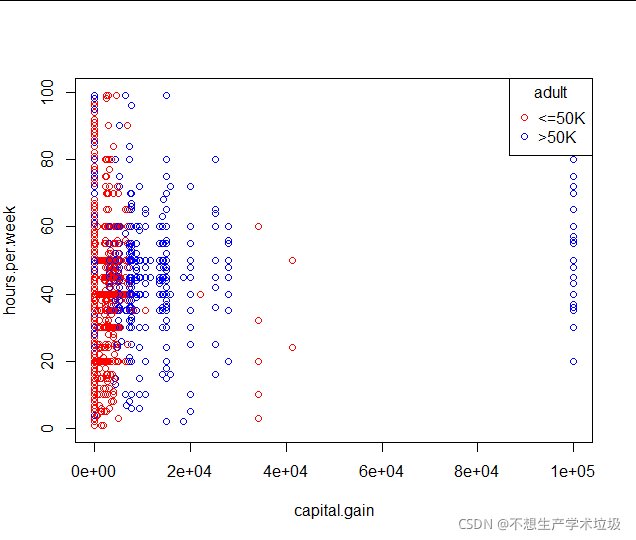(j)capital.loss和hours.per.week散点图

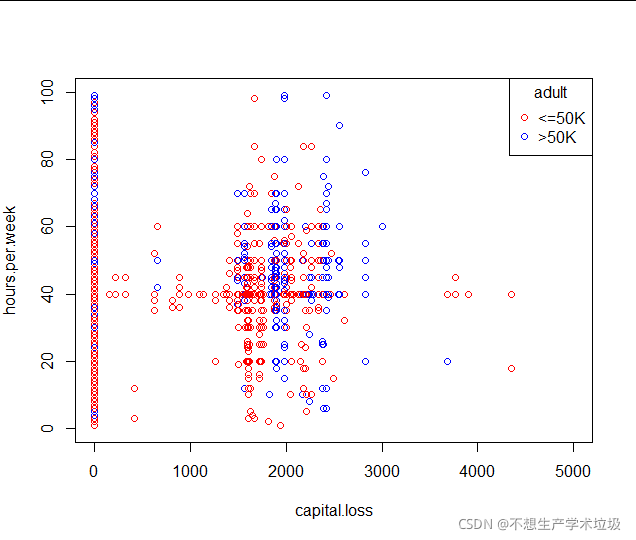
（4）结果解释

(a)age和education.num散点图
一般来说，受教育时间越长收入越高，一般与年龄关系不大，不过可以看出会存在一部分中年人虽然受教育时间短但是收入却很高，说明教育程度不是导致一个人收入高的必然因素。

(b)age和capital.gain散点图
投资收益高，其收入越高，与年龄关系不大

(c)age和capital.loss散点图
投资损失很大时，倾向于收入低，但是损失不大时，与收入似乎没有必然的关系，年龄不影响这样的分布

(d)age和hours.per.week散点图
高收入和每周工作时间没有太大的必然关系，反而在中青年群体中分布较多

(e)education.num和capital.gain散点图
投资收益低更倾向于低收入，当投资收益不低时，受教育时间越长，高收入比例越高。

(f)education.num和capital.loss散点图
对于受教育时间短的人来说，投资损失会对收入造成很大影响，而对于受教育时间长的人来说影响不大。

(g)education.num和hours.per.week散点图
这个结论很有趣：在受教育时间短的情况下，每周工作时间越长，收入会越高，但是在受教育时间足够长后，收入就与每周工作时间没有太大的关系了。

(h)capital.gain和captal.loss散点图
可以看到两者是互斥的关系，如果投资盈利，一定不会损失。此外，投资的情况一般和收入没有必然的联系。

(i)capital.gain和hours.per.week散点图
投资收益较少时，提高工作时间会小幅度提高收入，但是当投资收益提高时，高收入比例会迅速提高。

(j)capital.loss和hours.per.week散点图
投资损失不会必然造成低收入，没有太多的规律

10.挑选数据集的子集

第32题：基于目前的探索，在数据集中选出那些接下来值得进一步探索的子集
基于以上的探索结果，可以探索教育程度、从事职业和每周工作时间进行探索，因为之前已经发现，在教育程度很高的情况下，获取高收入其实和每周工作时间没有太大的关系了，那么我们可以探索什么样的工作性质、职位能够提供这种需要高的教育程度、对工作时间不需要很多的职位。

11.对数值变量进行分箱

第33题：对一个数值变量进行分箱，要求这样：分箱使得不同类之间的差别最小化

（1）实验代码

k_means <- kmeans(adult$demogweight, 3)
adult$demog_cluster = k_means$cluster
plot(adult$demogweight,col=adult$demog_cluster)

（2）原理介绍

下图分别为等宽、等频、K-means聚类的示意图

（3）实验结果

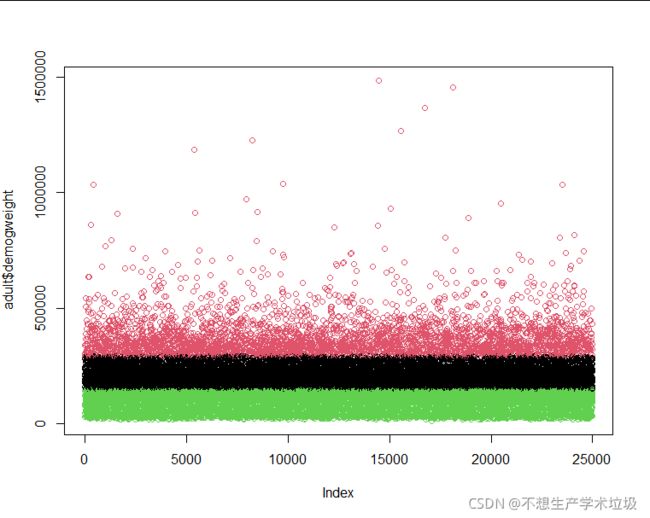
（4）结果解释

横坐标是一个record的行号，纵坐标是其demogweight的值，聚类结果用不同颜色来表示，可以看到取值近似的点他们被分到了同一个类。

12.使用另外两种分箱方法进行分箱

（1）实验代码

# 等宽 equal width分箱
demog_width<- discretize(adult$demogweight,"equalwidth",3)
plot(adult$demogweight,col=demog_width$X+1)

# 等数量equal number of records分箱
demog_number<- discretize(adult$demogweight,"equalfreq",3)
plot(adult$demogweight,col=demog_number$X+1)

（2）原理介绍

无

（3）实验结果

等宽度分箱：
等频度分箱：

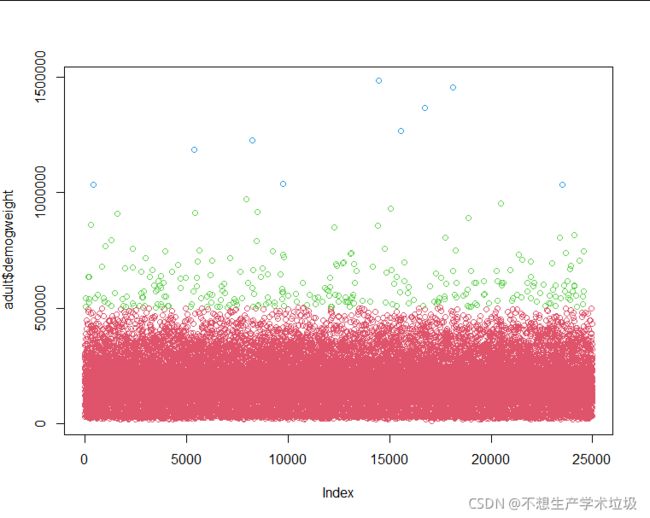
（4）结果解释

等宽度分箱时，如果在不同箱内数据的分布不同，那么就会出现一些箱过于庞大，一些又过于小，也即尽管保证了分箱的数值区间的均匀，但是不能保证每个箱内样本数量均匀。
等频度分箱时，也会受到数据分布的影响，如果在某一区间分布的点过多，那么这个区间就会趋向于包含不同频度的划分范围，即尽管保证了每个箱内样本数量均匀，但不能保证分箱的数值区间的均匀
因此比较而言，感觉用K-means进行分箱比较好。

13.总结数据探索阶段的收获

题35
通常的数据中观测变量分为分类变量和连续变量。在数据探索阶段，分类变量往往能对于目标变量能有更为直观的影响体现，如工资的收入和受教育 的学历、婚姻关系、性别以及种族有关，工资也与职位、从事哪种性值的工作有关，而跟工作者的国籍没有太大的关系。
连续性数字变量往往取值较多，但是能表达出连续的数字变化对于目标变量的影响，如随着受教育时间的增多，高收入人群所占的比例在逐渐升高。