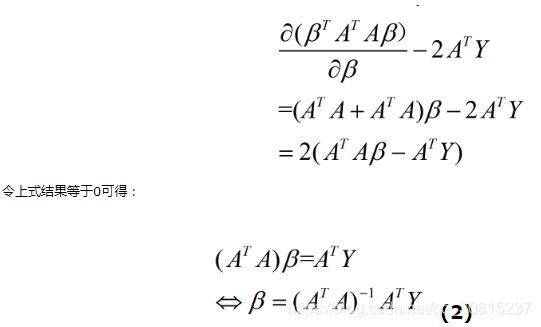RANSAC与圆柱拟合

RANSAC是“RANdom SAmple Consensus（随机抽样一致）”的缩写。它可以从一组包含“局外点”的观测数据集中，通过迭代方式估计数学模型的参数。它是一种不确定的算法——它有一定的概率得出一个合理的结果；为了提高概率必须提高迭代次数。该算法最早由Fischler和Bolles于1981年提出。
    RANSAC的基本假设是：
（1）数据由“局内点”组成，例如：数据的分布可以用一些模型参数来解释；
（2）“局外点”是不能适应该模型的数据；
（3）除此之外的数据属于噪声。 局外点产生的原因有：噪声的极值；错误的测量方法；对数据的错误假设。

    RANSAC也做了以下假设：给定一组（通常很小的）局内点，存在一个可以估计模型参数的过程；而该模型能够解释或者适用于局内点。

一、RANSAC理论介绍

普通最小二乘是保守派：在现有数据下，如何实现最优。是从一个整体误差最小的角度去考虑，尽量谁也不得罪。

RANSAC是改革派：首先假设数据具有某种特性（目的），为了达到目的，适当割舍一些现有的数据。

给出最小二乘拟合（红线）、RANSAC（绿线）对于一阶直线、二阶曲线的拟合对比：

                                           

可以看到RANSAC可以很好的拟合。RANSAC可以理解为一种采样的方式，所以对于多项式拟合、混合高斯模型（GMM）等理论上都是适用的。

      一个简单的例子如下：简单的最小二乘法不能找到适应于局内点的直线，原因是最小二乘法尽量去适应包括局外点在内的所有点。相反，RANSAC能得出一个仅仅用局内点计算出模型，并且概率还足够高。但是，RANSAC并不能保证结果一定正确，为了保证算法有足够高的合理概率，我们必须小心的选择算法的参数。

二、概述

  RANSAC算法的输入是一组观测数据，一个可以解释或者适应于观测数据的参数化模型，一些可信的参数。

RANSAC通过反复选择数据中的一组随机子集来达成目标。被选取的子集被假设为局内点，并用下述方法进行验证：
    1.有一个模型适应于假设的局内点，即所有的未知参数都能从假设的局内点计算得出。
    2.用1中得到的模型去测试所有的其它数据，如果某个点适用于估计的模型，认为它也是局内点。
    3.如果有足够多的点被归类为假设的局内点，那么估计的模型就足够合理。
    4.然后，用所有假设的局内点去重新估计模型，因为它仅仅被初始的假设局内点估计过。
    5.最后，通过估计局内点与模型的错误率来评估模型。
这个过程被重复执行固定的次数，每次产生的模型要么因为局内点太少而被舍弃，要么因为比现有的模型更好而被选用。

三、算法

输入：
data —— 一组观测数据
model —— 适应于数据的模型
n —— 适用于模型的最少数据个数
k —— 算法的迭代次数
t —— 用于决定数据是否适应于模型的阀值
d —— 判定模型是否适用于数据集的数据数目
输出：
best_model —— 跟数据最匹配的模型参数（如果没有找到好的模型，返回null）
best_consensus_set —— 估计出模型的数据点
best_error —— 跟数据相关的估计出的模型错误

iterations = 0
best_model = null
best_consensus_set = null
best_error = 无穷大
while ( iterations < k )
    maybe_inliers = 从数据集中随机选择n个点
    maybe_model = 适合于maybe_inliers的模型参数
    consensus_set局内点 = maybe_inliers

    for ( 每个数据集中不属于maybe_inliers的点 ）
        if ( 如果点适合于maybe_model，且错误小于t ）
            将点添加到consensus_set局内点
    if （ consensus_set中的元素数目大于d ）
        已经找到了好的模型，现在测试该模型到底有多好
        better_model = 用所有consensus_set拟合得到模型参数
        this_error = better_model计算该模型的拟合误差（就是cost，一般直接采用每个点的误差相加求和作为总cost）改进它就会变成MSAC
        if ( this_error < best_error )
            我们发现了比以前好的模型，保存该模型直到更好的模型出现
            best_model =  better_model
            best_consensus_set = consensus_set
            best_error =  this_error
    增加迭代次数
返回 best_model, best_consensus_set, best_error

from：https://www.cnblogs.com/xrwang/archive/2011/03/09/ransac-1.html

四、RANSAC简化版流程实例：

第一步：假定模型（如直线方程），并随机抽取Nums个（以2个为例）样本点，对模型进行拟合：

                                            

第二步：由于不是严格线性，数据点都有一定波动，假设容差范围为：sigma，找出距离拟合曲线容差范围内的点，并统计点的个数：

                                                      

第三步：重新随机选取Nums个点，重复第一步~第二步的操作，直到结束迭代：

                                                    

第四步：每一次拟合后，容差范围内都有对应的数据点数，找出数据点个数最多的情况，就是最终的拟合结果：

                                 

其实RANSAC忽略了几个问题：

• 每一次随机样本数Nums的选取：如二次曲线最少需要3个点确定，一般来说，Nums少一些易得出较优结果；
• 抽样迭代次数Iter的选取：即重复多少次抽取，就认为是符合要求从而停止运算？太多计算量大，太少性能可能不够理想；
• 容差Sigma的选取：sigma取大取小，对最终结果影响较大；

RANSAC的作用有点类似：将数据一切两段，一部分是自己人，一部分是敌人，自己人留下商量事，敌人赶出去。RANSAC开的是家庭会议，不像最小二乘总是开全体会议。

from：https://www.cnblogs.com/xingshansi/p/6763668.html

五、优点与缺点

    RANSAC的优点是它能鲁棒的估计模型参数。例如，它能从包含大量局外点的数据集中估计出高精度的参数。RANSAC的缺点是它计算参数的迭代次数没有上限；如果设置迭代次数的上限，得到的结果可能不是最优的结果，甚至可能得到错误的结果。RANSAC只有一定的概率得到可信的模型，概率与迭代次数成正比。RANSAC的另一个缺点是它要求设置跟问题相关的阀值。
    RANSAC只能从特定的数据集中估计出一个模型，如果存在两个（或多个）模型，RANSAC不能找到别的模型。

六、改进RANSAC——MSAC

     RANSAC与MSAC唯一的区别在于cost的计算方式。RANSAC对于阈值（Tolerance）选取过于敏感，这个值过大了算法就无效了，过小的话算法会变得很不稳定。而MSAC可以做到部分补偿这些负面影响。

RANSAC的cost算法伪代码：

count = 局内点个数 
cost = 0
For (n=0; n

   对于每个局内点，计算它与拟合模型的误差，误差小于Tolerance，将误差值视为cost；误差大于Tolerance，则将“1”设为cost；将所有局内点的cost相加作为总cost。

MSAC的cost算法伪代码：

count = 局内点个数
cost = 0
For (n=0; n

    对于每个局内点，计算它与拟合模型的误差，误差小于Tolerance，将误差值视为cost；误差大于Tolerance，则将Tolerance设为cost；将所有局内点的cost相加作为总cost。

from：https://blog.csdn.net/weixin_44558898/article/details/88986497

在MATLAB中：

 % Evaluate model with truncated loss评估具有截断损失
 dis = evalFunc(modelParams, allPoints);
 dis(dis > threshold) = threshold;
 accDis = sum(dis);

补充：三维RANSAC

matlab2018中的ransac源码:

% Load and plot a set of noisy 2D points.
%  load 'pointsForLineFitting.mat';
%  plot(points(:,1), points(:,2), '*');
%  hold on
%
%  % Fit a line using linear least squares.
%  modelLeastSquares = polyfit(points(:,1), points(:,2), 1);
%  x = [min(points(:,1)), max(points(:,1))];
%  y = modelLeastSquares(1)*x + modelLeastSquares(2);
%  plot(x, y, 'r-');
%
%  % Fit a line to the points using M-estimator SAmple Consensus algorithm.
%  sampleSize = 2;
%  maxDistance = 2;
%  fitLineFcn  = @(points) polyfit(points(:,1), points(:,2), 1);
%  evalLineFcn = ...
%     @(model, points) sum((points(:, 2) - polyval(model, points(:,1))).^2, 2);
%     
%  [modelRANSAC, inlierIdx] = RANSAC(points, fitLineFcn, evalLineFcn, ...
%     sampleSize, maxDistance);
%
%  % Re-fit a line to the inliers.
%  modelInliers = polyfit(points(inlierIdx,1), points(inlierIdx,2), 1);
%
%  % Display the line.
%  inlierPts = points(inlierIdx, :);
%  x = [min(inlierPts(:,1)); max(inlierPts(:,1))];
%  y = modelInliers(1)*x + modelInliers(2);
%  plot(x, y, 'g-');
%  legend('Noisy Points', 'Least Squares Fit', 'Robust Fit');
%  hold off

1、空间直线：已知两个点即可确定一条直线：

     点向式：(x-x0）/u =（y-y0）/v=(z-z0) /w ，过点（x0,y0,z0） ,且有方向向量（u,v,w)。

     设空间一点为P(x0,y0,z0)，在直线上找一点Q(x1,y1,z1)，直线的方向向量为:S=(l,m,n)，则d=|PQ叉乘S|/|S|，

理由:|PQ叉乘S|为一平行四边形的面积,|S|为其一边.故=|PQ叉乘S|/|S|为平行四边形的高.即为点到直线的距离。

2、空间平面：三个不在一条直线上的点确定一个平面

Ax+By+Cz+D=0，即ax+by+cz+1=0

四个未知数求出三个就够啦,这三个未知数都可以用第四个未知数来表示,假设第四个未知数是D.则求出来的三个未知数一般是：A=a*D;B=b*D;C=c*D;（D不等于0），最终有a*Dx+b*Dy+cDz+D=0,等式两边同除以D,得平面方程ax+by+cz+1=0；

将已知三个点的坐标分别用P1(x1,y1,z1)，P2(x2,y2,z2)，P3(x3,y3,z3)表示。

设通过P1，P2，P3三点的平面方程为：Ax + By + Cz + D = 0。将P1(x1,y1,z1)点数值代入方程Ax + By + Cz + D = 0。

即可得到：Ax1 + By 1+ Cz1 + D = 0。化简得D = -(A * x1 + B * y1 + C * z1)。

则可以根据P1(x1,y1,z1)，P2(x2,y2,z2)，P3(x3,y3,z3)三点坐标分别求得A、B、C的值，如下：

A = (y3 - y1)*(z3 - z1) - (z2 -z1)*(y2 - y1);

B = (x3 - x1)*(z2 - z1) - (x2 - x1)*(z3 - z1);

C = (x2 - x1)*(y3 - y1) - (x3 - x1)*(y2 - y1);

又D = -(A * x1 + B * y1 + C * z1)，所以可以求得D的值。

利用RANSAC拟合平面：

clc;clear all;close all;

%%%三维平面拟合
%%%生成随机数据
%内点
mu=[0 0 0];  %均值
S=[2 0 4;0 4 0;4 0 8];  %协方差
data1=mvnrnd(mu,S,300);   %产生200个高斯分布数据
%外点
mu=[2 2 2];
S=[8 1 4;1 8 2;4 2 8];  %协方差
data2=mvnrnd(mu,S,100);     %产生100个噪声数据
%合并数据
data=[data1',data2'];
iter = 1000; 

%%% 绘制数据点
 figure;plot3(data(1,:),data(2,:),data(3,:),'o');hold on; % 显示数据点
 number = size(data,2); % 总点数
 bestParameter1=0; bestParameter2=0; bestParameter3=0; % 最佳匹配的参数
 sigma = 1;
 pretotal=0;     %符合拟合模型的数据的个数

for i=1:iter
 %%% 随机选择三个点
     idx = randperm(number,3); 
     sample = data(:,idx); 

     %%%拟合直线方程 z=ax+by+c
     plane = zeros(1,3);
     x = sample(:, 1);
     y = sample(:, 2);
     z = sample(:, 3);

     a = ((z(1)-z(2))*(y(1)-y(3)) - (z(1)-z(3))*(y(1)-y(2)))/((x(1)-x(2))*(y(1)-y(3)) - (x(1)-x(3))*(y(1)-y(2)));
     b = ((z(1) - z(3)) - a * (x(1) - x(3)))/(y(1)-y(3));
     c = z(1) - a * x(1) - b * y(1);
     plane = [a b -1 c]

     mask=abs(plane*[data; ones(1,size(data,2))]);    %求每个数据到拟合平面的距离
     total=sum(maskpretotal            %找到符合拟合平面数据最多的拟合平面
         pretotal=total;
         bestplane=plane;          %找到最好的拟合平面
    end  
 end
 %显示符合最佳拟合的数据
mask=abs(bestplane*[data; ones(1,size(data,2))])

在编程中，我们知道三个空间点之后，可以用 [uu, dd, vv] = svd(A); plane = vv(:,end); plane = plane ./ plane(end); plane = plane';来快速求解法向量，确定一个空间平面。

from：https://blog.csdn.net/u010128736/article/details/53422070 

3、MATLAB中的圆柱拟合：初始模型参数表示为[x，y，z，dx，dy，dz，r]。其中（x，y，z）是圆柱中心轴上的一个点，（dx，dy，dz）指定轴的方向，r是半径。

• 第一步：每次随机选两个点P0,P1，这两个点在拟合圆柱的表面上。用于拟合中心轴和半径：

输入是2*6的矩阵，每行代表一个样本，每行的前3列代表x,y,z,后三行代表该点的法向量。

function model = fitCylinder(points)
p1 = points(1,1:3);
n1 = points(1,4:6);
p2 = points(2,1:3);
n2 = points(2,4:6);
w = p1 + n1 - p2;

a = n1 * n1';%模
b = n1 * n2';%点乘
c = n2 * n2';%模
d = n1 * w';
e = n2 * w';
D = a * c - b * b;
if abs(D) < 1e-5
    s = 0;
    if b > c
        t = d / b;
    else
        t = e / c;
    end
else
    s = (b * e - c * d) / D;
    t = (a * e - b * d) / D;
end

% P0 is a point on the axis
p0 = p1 + n1 + s * n1;
% dp is a normalized vector for the direction of the axis
dp = p2 + t * n2 - p0;%（p2 + t * n2） - p0
dp = dp / norm(dp);

p1p0 = p1 - p0;
p2p1 = dp;
c = [p1p0(2)*p2p1(3) - p1p0(3)*p2p1(2), ...
     p1p0(3)*p2p1(1) - p1p0(1)*p2p1(3), ...
     p1p0(1)*p2p1(2) - p1p0(2)*p2p1(1)];%就是p1p0,p2p1两向量的叉乘，a*b*cos,模表示两向量围成的平行四边形的面积
% p2p1 is a unit vector, so the denominator is not needed ，p2p1是单位向量，模为1，
r = sqrt(sum(c.*c, 2));%即c的模（面积）就是高，也就是半径

model = [p0, dp, r];

• 第二步：根据模型参数，然后求全体点云中的每个点P0到中心轴的距离。

function dis = evalCylinder(model, points)
p1p0 = [points(:,1)-model(1), points(:,2)-model(2), points(:,3)-model(3)];
p2p1 = model(4:6);
c = [p1p0(:,2)*p2p1(3) - p1p0(:,3)*p2p1(2), ...
     p1p0(:,3)*p2p1(1) - p1p0(:,1)*p2p1(3), ...
     p1p0(:,1)*p2p1(2) - p1p0(:,2)*p2p1(1)];
% p2p1 is a unit vector, so the denominator is not needed
D = sum(c.*c, 2);
dis = abs(sqrt(D) - model(7));#求得是误差error

• 第三步：计算损失，通过总损失来衡量模型的拟合好坏

        % Evaluate model with truncated loss评估具有截断损失
        dis = evalFunc(modelParams, allPoints);
        dis(dis > threshold) = threshold;
        accDis = sum(dis);

实例：

                             

points=[1,1,0,1,0,0;1,2,0,1,0,0]
p1 = points(1,1:3);
n1 = points(1,4:6);
p2 = points(2,1:3);
n2 = points(2,4:6);
w = p1 + n1 - p2;

a = n1 * n1';%模
b = n1 * n2';%点乘，标量
c = n2 * n2';%模
d = n1 * w';
e = n2 * w';
D = a * c - b * b;
if abs(D) < 1e-5
    s = 0;
    if b > c
        t = d / b;
    else
        t = e / c;
    end
else
    s = (b * e - c * d) / D;
    t = (a * e - b * d) / D;
end

% P0 is a point on the axis
p0 = p1 + n1 + s * n1;
% dp is a normalized vector for the direction of the axis
dp = p2 + t * n2 - p0;%（p2 + t * n2） - p0
dp = dp / norm(dp);

p1p0 = p1 - p0;
p2p1 = dp;
c = [p1p0(2)*p2p1(3) - p1p0(3)*p2p1(2), ...
     p1p0(3)*p2p1(1) - p1p0(1)*p2p1(3), ...
     p1p0(1)*p2p1(2) - p1p0(2)*p2p1(1)];%就是p1p0,p2p1两向量的叉乘，a*b*sin,模表示两向量围成的平行四边形的面积
% p2p1 is a unit vector, so the denominator is not needed ，p2p1是单位向量，模为1，
r = sqrt(sum(c.*c, 2));%求c的模（表示两向量围成的平行四边形的面积）因为这里p2p1是单位向量，所以面积就是高，也就是半径

model = [p0, dp, r];

不行，还是看不懂MATLAB到底是怎么拟合圆柱了，求助！！！会的请留言给我，谢谢

圆柱拟合：

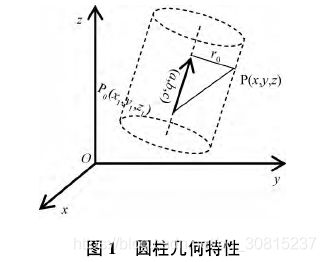
      由圆柱面的几何特性可得，圆柱面上的点到其轴线的距离恒等于半径 r0，其中，P 为圆柱面上任意一点，P0( x0，y0，z0) 为圆柱轴线上一点， ( a，b，c) 为圆柱轴线向量，r0为圆柱底圆半径。圆柱面上任意一点到其轴线的距离为半径 r0，即:

                                     

求出这七个参数，就可以唯一确定一个圆柱。
 

                                            

     圆柱拟合步骤主要包括两步: 一是确定柱面模型参数初始值; 二是建立误差方程式求解参数值。本文算法结合主成分分析法与线性最小二乘法，确定圆 柱 轴 线 向 量 ( a，b，c) 、圆 柱 轴 线 上 一 点( x1，y1，z1) 、圆柱底圆半径 r 这七个柱面模型参数初始值，再建立改进误差方程式，求解参数。

本文柱面拟合方法详细步骤如下:

1、确定柱面模型参数初始值。

     搜寻圆柱面上任意一点的若干邻近点，将这些点拟合成平面，得到的平面法向量单位化即该点的单位法向量。对圆柱面上每个点处理，得到每个点的单位法向量。将每个点的单位法向量看成点，将这些点拟合成平面，得到平面法向量，即圆柱轴线向量初始值 a0、b0、c0，该步骤使用了主成分分析法进行求解。（这一步和matlab源码很相似，matlab使用两个点，及它们的法向量来拟合圆柱。） 得到轴线后，对圆柱进行坐标转换，使圆柱轴线向量 ( a0，b0，c0) 变 换 为 平 行 Z 轴 的 向 量 ，这样圆柱面上的点的（x,y）坐标就是一个平面圆形，用他们拟合圆心，即( x1，y1，z1)和半径r.

2、建立误差方程。

                                      

将误差方程写成矩阵形式，要让V最小，接近0：

                                                  

from：https://www.cnblogs.com/wangkundentisy/p/7505487.html 

用最小二乘法求解， Ax=0的最小二乘解，即为求解的最小特征值对应的特征向量。这是一个循环的迭代过程，每一次迭代过程中代入的初值都等于上一次的初值加上求出的 X 的改正值，当 X 的数值小到满足要求的精度时退出迭代。

                                                     

代码：

for (int i = 0; i < size; i++) {
float x = cloud_in->points[i].x;
float y = cloud_in->points[i].y;
float z = cloud_in->points[i].z;
 
f0 = pow(x - x0, 2) + pow(y - y0, 2) + pow(z - z0, 2) - pow((a0*(x - x0) + b0 * (y - y0) + c0 * (z - z0)), 2) - r0 * r0;
L(i, 0) = -f0;
B(i, 0) = (a0 * (a0*(x - x0) + b0 * (y - y0) + c0 * (z - z0)) - (x - x0)) * 2;
B(i, 1) = (b0 * (a0*(x - x0) + b0 * (y - y0) + c0 * (z - z0)) - (y - y0)) * 2;
B(i, 2) = (c0 * (a0*(x - x0) + b0 * (y - y0) + c0 * (z - z0)) - (z - z0)) * 2;
B(i, 3) = -(a0*(x - x0) + b0 * (y - y0) + c0 * (z - z0))*(x - x0) * 2;
B(i, 4) = -(a0*(x - x0) + b0 * (y - y0) + c0 * (z - z0))*(y - y0) * 2;
B(i, 5) = -(a0*(x - x0) + b0 * (y - y0) + c0 * (z - z0))*(z - z0) * 2;
B(i, 6) = -2*r0;
}

X = B.colPivHouseholderQr().solve(L);，求解 L=BX，用最小二乘法求解X。

 PCL实现：

        PCL库自带的圆柱模型拟合，由于在查找最佳圆柱面的过程中会过滤很多点，因此考虑利用最小二乘的模型来拟合最接近实际点云的一个圆柱面，code如下：

#include "pch.h"
#include 
#include
#include
#include
#include
#include
#include
#include
#include
 
 
// use ransanc to fit cylinder
int fitCylinder(pcl::PointCloud::Ptr cloud_in, pcl::PointCloud::Ptr &cloud_out) {
	// Create segmentation object for cylinder segmentation and set all the parameters
	pcl::ModelCoefficients::Ptr coeffients_cylinder(new pcl::ModelCoefficients);
	pcl::PointIndices::Ptr inliers_cylinder(new pcl::PointIndices);
 
	//  Normals
	pcl::search::Search::Ptr tree = boost::shared_ptr>(new pcl::search::KdTree);
	pcl::PointCloud::Ptr normalsFilter(new pcl::PointCloud);
	pcl::NormalEstimation normalEstimator;
	normalEstimator.setSearchMethod(tree);
	normalEstimator.setInputCloud(cloud_in);
	normalEstimator.setKSearch(30);
	normalEstimator.compute(*normalsFilter);
	
	pcl::SACSegmentationFromNormals seg;
	seg.setOptimizeCoefficients(true);
	seg.setModelType(pcl::SACMODEL_CYLINDER);
	seg.setMethodType(pcl::SAC_RANSAC);
	//seg.setNormalDistanceWeight(0.1);
	seg.setNormalDistanceWeight(0.2);		// for coarse data
	seg.setMaxIterations(1000);
	seg.setDistanceThreshold(0.3);
	seg.setRadiusLimits(0, 6);				// radius is within 8 centimeters
	seg.setInputCloud(cloud_in);
	seg.setInputNormals(normalsFilter);
 
	// Perform segment
	seg.segment(*inliers_cylinder, *coeffients_cylinder);
	std::cerr << "Cylinder coefficient: " << *coeffients_cylinder << std::endl;
	
	// Ouput extracted cylinder
	pcl::ExtractIndices extract;
	extract.setInputCloud(cloud_in);
	extract.setIndices(inliers_cylinder);
	extract.filter(*cloud_out);
	pcl::PCDWriter wr;
	wr.write("Extract_Cylinder.pcd", *cloud_out);
 
	float sum_D = 0.0;
	float sum_Ave = 0.0;
	float x0 = coeffients_cylinder->values[0];
	float y0 = coeffients_cylinder->values[1];
	float z0 = coeffients_cylinder->values[2];
	float l = coeffients_cylinder->values[3];
	float m= coeffients_cylinder->values[4];
	float n = coeffients_cylinder->values[5];
	float r0 = coeffients_cylinder->values[6];
	for (int i = 0; i < cloud_out->points.size(); i++) {
		float x = cloud_out->points[i].x;
		float y = cloud_out->points[i].y;
		float z = cloud_out->points[i].z;
		// D=part1+part2
		float part1 = pow(x - x0, 2) + pow(y - y0, 2) + pow(z - z0, 2) - pow(r0, 2);
		float part2 = -pow(l*(x - x0) + m * (y - y0) + n * (z - z0), 2) / (l*l + m * m + n * n);
		sum_D +=pow( part1 + part2,2);
		sum_Ave += fabs(part1 + part2);
	}
	std::cerr << "The average difference is " << sum_Ave / cloud_out->points.size() << std::endl;;
	std::cerr << "The Difference of average difference is " << sum_D / cloud_out->points.size() << std::endl;;
	// evaluate the cylinder quation
 
}

from：https://blog.csdn.net/zhangxz259/article/details/86711348

参考论文：一种圆柱面拟合方法 ，袁建刚，潘轶