NNDL 实验六 卷积神经网络(2)基础算子
5.2 卷积神经网络的基础算子
![]()
我们先实现卷积网络的两个基础算子:卷积层算子和汇聚层算子。
5.2.1 卷积算子
卷积层是指用卷积操作来实现神经网络中一层。
为了提取不同种类的特征,通常会使用多个卷积核一起进行特征提取。
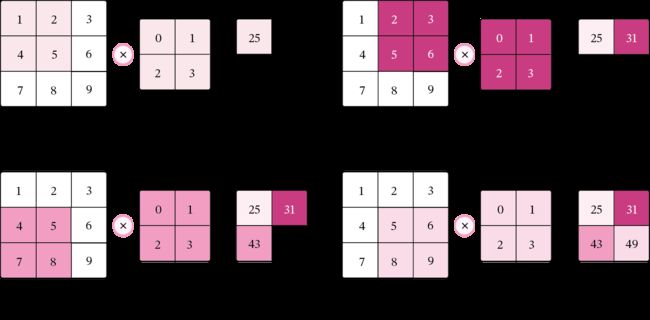
5.2.1.1 多通道卷积
5.2.1.2 多通道卷积层算子
代码实现:
import torch
import torch.nn as nn
class Conv2D(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0,
weight_attr=torch.ones,
bias_attr=torch.zeros):
super(Conv2D, self).__init__()
# 创建卷积核
self.weight = nn.Parameter(weight_attr([out_channels, in_channels, kernel_size, kernel_size]))
# 创建偏置
self.bias = nn.Parameter(bias_attr([out_channels, 1]))
self.stride = stride
self.padding = padding
# 输入通道数
self.in_channels = in_channels
# 输出通道数
self.out_channels = out_channels
# 基础卷积运算
def single_forward(self, X, weight):
# 零填充
new_X = torch.zeros([X.shape[0], X.shape[1] + 2 * self.padding, X.shape[2] + 2 * self.padding])
new_X[:, self.padding:X.shape[1] + self.padding, self.padding:X.shape[2] + self.padding] = X
u, v = weight.shape
output_w = (new_X.shape[1] - u) // self.stride + 1
output_h = (new_X.shape[2] - v) // self.stride + 1
output = torch.zeros([X.shape[0], output_w, output_h])
for i in range(0, output.shape[1]):
for j in range(0, output.shape[2]):
output[:, i, j] = torch.sum(
new_X[:, self.stride * i:self.stride * i + u, self.stride * j:self.stride * j + v] * weight,dim=[1, 2])
return output
def forward(self, inputs):
"""
输入:
- inputs:输入矩阵,shape=[B, D, M, N]
- weights:P组二维卷积核,shape=[P, D, U, V]
- bias:P个偏置,shape=[P, 1]
"""
feature_maps = []
# 进行多次多输入通道卷积运算
p = 0
for w, b in zip(self.weight, self.bias): # P个(w,b),每次计算一个特征图Zp
multi_outs = []
# 循环计算每个输入特征图对应的卷积结果
for i in range(self.in_channels):
single = self.single_forward(inputs[:, i, :, :], w[i])
multi_outs.append(single)
# print("Conv2D in_channels:",self.in_channels,"i:",i,"single:",single.shape)
# 将所有卷积结果相加
feature_map = torch.sum(torch.stack(multi_outs), dim=0) + b # Zp
feature_maps.append(feature_map)
# print("Conv2D out_channels:",self.out_channels, "p:",p,"feature_map:",feature_map.shape)
p += 1
# 将所有Zp进行堆叠
out = torch.stack(feature_maps, 1)
return out
inputs = torch.tensor([[[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]]])
conv2d = Conv2D(in_channels=2, out_channels=3, kernel_size=2)
print("inputs shape:", inputs.shape)
outputs = conv2d(inputs)
print("Conv2D outputs shape:", outputs.shape)
# 比较与torch API运算结果
conv2d_torch = nn.Conv2d(in_channels=2, out_channels=3, kernel_size=(2,2))
conv2d_torch.weight.data = torch.ones([3,2,2,2])
conv2d_torch.bias.data = torch.zeros([3])
outputs_torch=conv2d_torch(inputs)
# 自定义算子运算结果
print('Conv2D outputs:', outputs)
# torch API运算结果
print('nn.Conv2D outputs:', outputs_torch)结果如下:
inputs shape: torch.Size([1, 2, 3, 3])
Conv2D outputs shape: torch.Size([1, 3, 2, 2])
Conv2D outputs: tensor([[[[20., 28.],
[44., 52.]],
[[20., 28.],
[44., 52.]],
[[20., 28.],
[44., 52.]]]], grad_fn=)
nn.Conv2D outputs: tensor([[[[20., 28.],
[44., 52.]],
[[20., 28.],
[44., 52.]],
[[20., 28.],
[44., 52.]]]], grad_fn=) 自定义算子与框架中的算子相同,运行效果一样。
5.2.1.3 卷积算子的参数量和计算量
参数量
对于大小为D×M×N的输入特征图,使用PP组大小为![]() 的卷积核进行卷积运算,参数量计算方式为:
的卷积核进行卷积运算,参数量计算方式为:
parameters=P×D×U×V+P.(5.20)
其中,最后的P代表偏置个数。例如:输入特征图大小为3×32×3,使用6组大小为3×3×3的卷积核进行卷积运算,参数量为:
parameters=6×3×3×3+6=168.
计算量
对于大小为D×M×N的输入特征图,使用PP组大小为![]() 的卷积核进行卷积运算,计算量计算方式为:
的卷积核进行卷积运算,计算量计算方式为:
FLOPs=M′×N′×P×D×U×V+M′×N′×P。(5.21)
其中M′×N′×P代表加偏置的计算量,即输出特征图上每个点都要与PP组卷积核![]() 进行U×V×D次乘法运算后再加上偏置。比如对于输入特征图大小为3×32×32,使用6组大小为3×3×3的卷积核进行卷积运算,计算量为:
进行U×V×D次乘法运算后再加上偏置。比如对于输入特征图大小为3×32×32,使用6组大小为3×3×3的卷积核进行卷积运算,计算量为:
FLOPs=M′×N′×P×D×U×V+M′×N′×P=30×30×3×3×6×3+30×30×6=151200
5.2.2 汇聚层算子
汇聚层的作用是进行特征选择,降低特征数量,从而减少参数数量。由于汇聚之后特征图会变得更小,如果后面连接的是全连接层,可以有效地减小神经元的个数,节省存储空间并提高计算效率。
常用的汇聚方法有两种,分别是:平均汇聚和最大汇聚。
![]()
代码实现如下:
import torch
import torch.nn as nn
class Conv2D(nn.Module):
def __init__(self, in_channels, out_channels, kernel_size, stride=1, padding=0,
weight_attr=torch.ones,
bias_attr=torch.zeros):
super(Conv2D, self).__init__()
# 创建卷积核
self.weight = nn.Parameter(weight_attr([out_channels, in_channels, kernel_size, kernel_size]))
# 创建偏置
self.bias = nn.Parameter(bias_attr([out_channels, 1]))
self.stride = stride
self.padding = padding
# 输入通道数
self.in_channels = in_channels
# 输出通道数
self.out_channels = out_channels
# 基础卷积运算
def single_forward(self, X, weight):
# 零填充
new_X = torch.zeros([X.shape[0], X.shape[1] + 2 * self.padding, X.shape[2] + 2 * self.padding])
new_X[:, self.padding:X.shape[1] + self.padding, self.padding:X.shape[2] + self.padding] = X
u, v = weight.shape
output_w = (new_X.shape[1] - u) // self.stride + 1
output_h = (new_X.shape[2] - v) // self.stride + 1
output = torch.zeros([X.shape[0], output_w, output_h])
for i in range(0, output.shape[1]):
for j in range(0, output.shape[2]):
output[:, i, j] = torch.sum(
new_X[:, self.stride * i:self.stride * i + u, self.stride * j:self.stride * j + v] * weight,
dim=[1, 2])
return output
def forward(self, inputs):
"""
输入:
- inputs:输入矩阵,shape=[B, D, M, N]
- weights:P组二维卷积核,shape=[P, D, U, V]
- bias:P个偏置,shape=[P, 1]
"""
feature_maps = []
# 进行多次多输入通道卷积运算
p = 0
for w, b in zip(self.weight, self.bias): # P个(w,b),每次计算一个特征图Zp
multi_outs = []
# 循环计算每个输入特征图对应的卷积结果
for i in range(self.in_channels):
single = self.single_forward(inputs[:, i, :, :], w[i])
multi_outs.append(single)
# print("Conv2D in_channels:",self.in_channels,"i:",i,"single:",single.shape)
# 将所有卷积结果相加
feature_map = torch.sum(torch.stack(multi_outs), dim=0) + b # Zp
feature_maps.append(feature_map)
# print("Conv2D out_channels:",self.out_channels, "p:",p,"feature_map:",feature_map.shape)
p += 1
# 将所有Zp进行堆叠
out = torch.stack(feature_maps, 1)
return out
inputs = torch.tensor([[[[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]],
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0], [7.0, 8.0, 9.0]]]])
conv2d = Conv2D(in_channels=2, out_channels=3, kernel_size=2)
outputs = conv2d(inputs)
# 比较与torch API运算结果
conv2d_torch = nn.Conv2d(in_channels=2, out_channels=3, kernel_size=(2, 2))
conv2d_torch.weight.data = torch.ones([3, 2, 2, 2])
conv2d_torch.bias.data = torch.zeros([3])
outputs_torch = conv2d_torch(inputs)
class Pool2D(nn.Module):
def __init__(self, size=(2, 2), mode='max', stride=1):
super(Pool2D, self).__init__()
# 汇聚方式
self.mode = mode
self.h, self.w = size
self.stride = stride
def forward(self, x):
output_w = (x.shape[2] - self.w) // self.stride + 1
output_h = (x.shape[3] - self.h) // self.stride + 1
output = torch.zeros([x.shape[0], x.shape[1], output_w, output_h])
# 汇聚
for i in range(output.shape[2]):
for j in range(output.shape[3]):
# 最大汇聚
if self.mode == 'max':
output[:, :, i, j] = torch.max(
x[:, :, self.stride * i:self.stride * i + self.w, self.stride * j:self.stride * j + self.h],
)
# 平均汇聚
elif self.mode == 'avg':
output[:, :, i, j] = torch.mean(
x[:, :, self.stride * i:self.stride * i + self.w, self.stride * j:self.stride * j + self.h],
dim=[2, 3])
return output
inputs = torch.tensor([[[[1., 2., 3., 4.], [5., 6., 7., 8.], [9., 10., 11., 12.], [13., 14., 15., 16.]]]])
pool2d = Pool2D(stride=2)
outputs = pool2d(inputs)
print("input: {}, \noutput: {}".format(inputs.shape, outputs.shape))
# 比较Maxpool2D与paddle API运算结果
maxpool2d_paddle = nn.MaxPool2d(kernel_size=(2, 2), stride=2)
outputs_paddle = maxpool2d_paddle(inputs)
# 自定义算子运算结果
print('Maxpool2D outputs:', outputs)
# paddle API运算结果
print('nn.Maxpool2D outputs:', outputs_paddle)
# 比较Avgpool2D与paddle API运算结果
avgpool2d_paddle = nn.AvgPool2d(kernel_size=(2, 2), stride=2)
outputs_paddle = avgpool2d_paddle(inputs)
pool2d = Pool2D(mode='avg', stride=2)
outputs = pool2d(inputs)
# 自定义算子运算结果
print('Avgpool2D outputs:', outputs)
# paddle API运算结果
print('nn.Avgpool2D outputs:', outputs_paddle)
结果如下:
input: torch.Size([1, 1, 4, 4]),
output: torch.Size([1, 1, 2, 2])
Maxpool2D outputs: tensor([[[[ 6., 8.],
[14., 16.]]]])
nn.Maxpool2D outputs: tensor([[[[ 6., 8.],
[14., 16.]]]])
Avgpool2D outputs: tensor([[[[ 3.5000, 5.5000],
[11.5000, 13.5000]]]])
nn.Avgpool2D outputs: tensor([[[[ 3.5000, 5.5000],
[11.5000, 13.5000]]]])
进程已结束,退出代码为 0
汇聚层的参数量和计算量
由于汇聚层中没有参数,所以参数量为0;
最大汇聚中,没有乘加运算,所以计算量为0,
平均汇聚中,输出特征图上每个点都对应了一次求平均运算。
使用pytorch实现Convolution Demo
卷积演示
下面是一个 CONV 层的运行演示。由于 3D 体积难以可视化,因此所有体积(输入体积(蓝色)、重量体积(红色)、输出体积(绿色))都可视化,每个深度切片堆叠成行。输入体积的大小为 W1=5,H1=5,D1=3,CONV 层参数为 K=2,F=3,S=2,P=1。也就是说,我们有两个大小为 3×3 的过滤器,它们以 2 的步幅应用。因此,输出卷大小具有空间大小 (5 - 3 + 2)/2 + 1 = 3。此外,请注意,P=1 的填充应用于输入体积,使输入音量的外部边界为零。下面的可视化效果循环访问输出激活(绿色),并显示每个元素的计算方法是将突出显示的输入(蓝色)与筛选器(红色)相乘,将其相加,然后通过偏差抵消结果。
![]()
代码实现
import torch
import torch.nn as nn
class Conv2D(nn.Module):
def __init__(self, in_channels, out_channels, stride, padding, weight, bias):
super(Conv2D, self).__init__()
# 创建卷积核
self.weight = nn.Parameter(weight)
# 创建偏置
self.bias = nn.Parameter(bias)
self.stride = stride
self.padding = padding
# 输入通道数
self.in_channels = in_channels
# 输出通道数
self.out_channels = out_channels
# 基础卷积运算
def single_forward(self, X, weight):
# 零填充
new_X = torch.zeros([X.shape[0], X.shape[1] + 2 * self.padding, X.shape[2] + 2 * self.padding])
new_X[:, self.padding:X.shape[1] + self.padding, self.padding:X.shape[2] + self.padding] = X
u, v = weight.shape
output_w = (new_X.shape[1] - u) // self.stride + 1
output_h = (new_X.shape[2] - v) // self.stride + 1
output = torch.zeros([X.shape[0], output_w, output_h])
for i in range(0, output.shape[1]):
for j in range(0, output.shape[2]):
output[:, i, j] = torch.sum(
new_X[:, self.stride * i:self.stride * i + u, self.stride * j:self.stride * j + v] * weight,
dim=[1, 2])
return output
def forward(self, inputs):
"""
输入:
- inputs:输入矩阵,shape=[B, D, M, N]
- weights:P组二维卷积核,shape=[P, D, U, V]
- bias:P个偏置,shape=[P, 1]
"""
feature_maps = []
# 进行多次多输入通道卷积运算
p = 0
for w, b in zip(self.weight, self.bias): # P个(w,b),每次计算一个特征图Zp
multi_outs = []
# 循环计算每个输入特征图对应的卷积结果
for i in range(self.in_channels):
single = self.single_forward(inputs[:, i, :, :], w[i])
multi_outs.append(single)
# print("Conv2D in_channels:",self.in_channels,"i:",i,"single:",single.shape)
# 将所有卷积结果相加
feature_map = torch.sum(torch.stack(multi_outs), dim=0) + b # Zp
feature_maps.append(feature_map)
# print("Conv2D out_channels:",self.out_channels, "p:",p,"feature_map:",feature_map.shape)
p += 1
# 将所有Zp进行堆叠
out = torch.stack(feature_maps, 1)
return out
inputs = torch.tensor([[[[0.0, 1.0, 1.0, 0.0, 2.0], [2.0, 2.0, 2.0, 2.0, 1.0], [1.0, 0.0, 0.0, 2.0, 0.0],
[0.0, 1.0, 1.0, 0.0, 0.0], [1.0, 2.0, 0.0, 0.0, 2.0]],
[[1.0, 0.0, 2.0, 2.0, 0.0], [0.0, 0.0, 0.0, 2.0, 0.0], [1.0, 2.0, 1.0, 2.0, 1.0],
[1.0, 0.0, 0.0, 0.0, 0.0], [1.0, 2.0, 0.0, 0.0, 2.0]],
[[2.0, 1.0, 2.0, 0.0, 0.0], [1.0, 0.0, 0.0, 1.0, 0.0], [0.0, 2.0, 1.0, 0.0, 1.0],
[0.0, 1.0, 2.0, 2.0, 2.0], [2.0, 1.0, 0.0, 0.0, 1.0]]]], dtype=torch.float32)
w = torch.tensor([[[[-1, 1, 0], [0, 1, 0], [0, 1, 1]],
[[-1, -1, 0], [0, 0, 0], [0, -1, 0]],
[[0, 0, -1], [0, 1, 0], [1, -1, -1]]],
[[[1, 1, -1], [-1, -1, 1], [0, -1, 1]],
[[0, 1, 0], [-1, 0, -1], [-1, 1, 0]],
[[-1, 0, 0], [-1, 0, 1], [-1, 0, 0]]]], dtype=torch.float32)
b = torch.tensor([1., 0.])
conv2d = Conv2D(in_channels=3, out_channels=2, stride=2, padding=1, weight=w, bias=b)
print("inputs shape:", inputs.shape)
outputs = conv2d(inputs)
print("Conv2D outputs shape:", outputs.shape)
print('Conv2D outputs:', outputs)
结果如下:
inputs shape: torch.Size([1, 3, 5, 5])
Conv2D outputs shape: torch.Size([1, 2, 3, 3])
Conv2D outputs: tensor([[[[ 6., 7., 5.],
[ 3., -1., -1.],
[ 2., -1., 4.]],
[[ 2., -5., -8.],
[ 1., -4., -4.],
[ 0., -4., -4.]]]], grad_fn=) 总结
本次实验主要是对多通道卷积算子进行实现实验,以及学习汇聚层算子参数量和计算量如何计算,在对这些知识的框架进行学习后其实本次实验已经可以说是完成了,但是我个人认为最后的选做题目是十分有意义的,本次的选做相当于为前面实验学习知识的巩固所给出的一道例题,在做完选做题后,我才真正感觉掌握了这节实验的知识。
参考
https://blog.csdn.net/qq_38975453/article/details/127189403?spm=1001.2014.3001.5502
https://www.cnblogs.com/hbuwyg/p/16617671.html