机器学习之进化算法

学习目标：

• 遗传算法基础
• 基因重组与基因突变
• 遗传算法实现技术
• 遗传算法实例

---

一、遗传算法

进化计算（Evolutionary Computation）包括遗传算法（Genetic Algorithm，GA）、进化策略（Evolutionary Strategies，ES）和基因编程（Genetic Programming）。进化进算是受进化生物学启发而发展起来的计算模型，其实现过程基于达尔文的物竞天择、适者生存的生物进化原理，通过将现实问题转化为基因染色体表示，并不断进行选择、交换、变异、复制等操作，逐步逼近最优结果，实现问题求解。遗传算法的本质是采用搜索方法来求解问题，并在目标函数的指导下控制搜索过程以求得最优解。进化策略与遗传算法类似，主要解决技术优化问题，例如某些问题改进策略未知或无法明确规则，它只包含变异操作。基因编程是遗传算法的扩展，将计算机程序作为进化对象，通过程序指令的组合、变异、复制等操作，实现机器自动化完成用户指定的任务。目前进化计算主要应用于机械工程、工业设计、生物学、生产调度等领域。

本文主要介绍遗传算法基本概念、实现方法等基础，并结合实例介绍与进化计算相关的蚁群算法和蜂群算法。

（一）遗传与变异

世间的生物从其亲代继承特性或性状，这种生命现象就称为遗传（Heredity）。

构成生物的基本结构和功能单位是细胞（Cell）。细胞中含有的一种微小的丝状化合物称为染色体（Chromosome），生物的所有遗传信息都包含在这个复杂而又微笑的染色体中。遗传信息是由基因（Gene）组成的。

在细胞分类的过程中，其遗传基因也同时被复制到下一代，从而其性状也被下一代所继承。

控制并决定生物遗传性状的染色体主要是由一种叫脱氧核糖核酸（DeoxyriboNucleic Acid，简称DNA）。DNA在染色体中有规则地排列。低等生物还含有一种叫做核糖核酸（Ribonucleic Acid，简称RNA）的物质。

基因就是DNA或RNA长链结构中占有一定位置的基本遗传单位。DNA中，遗传信息在一条长链上按一定的模式排列，亦即进行了遗传编码。

遗传基因在染色体中所占据的位置称为基因座（Locus），同一基因可能有的全部基因称为等位基因（Allele）。某种生物所特有的基因及其构成形式称为该生物的基因型（Genotype），而该生物在环境中呈现出相应的性状称为该生物的表现性（Phenotype）。一个细胞核中所有染色体所携带的遗传信息的全体称为一个基因组（Genome）。

在细胞分裂时，遗传物质DNA通过复制（Reproduction）而转移到新的细胞中，新细胞继承了旧细胞的基因。有性生殖生物在繁殖下一代时，两个同源染色体之间通过交叉（Crossover）而重组。

在进行细胞复制时，虽然概率很小，但也有可能产生某些复制差错，从而使DNA发生某种变异（Mutation），产生出新的染色体。

（二）进化

生物在其延续生存的过程中，逐渐适应于其生存环境，使得其品质不断得到改良，这种生命现象称为进化（Evolution）。生物的进化是以集团的形式共同进行的，这样的一个团体称为群体（Population）。组成群体的单个生物称为个体（Idvidual），每一个个体对其生存环境都有不同的适应能力，这个能力称为个体的适应度（Fitness）。

（三）遗传算法基本概念

遗传算法是进化计算的一个分支，是一种模拟自然界生物进化过程的随机搜索算法。遗传算法首先对问题进行描述，将潜在解进行编码，然后用随机数初始化一个种群，种群中的每个个体对应一个编码。最后通过适应度函数来度量个体的适应性，制定一种选择规则（选择函数f(x)），淘汰部分适应度较低的个体，并让优良的个体基因交叉复制和变异，产生新的子代。

与遗传算法相关的基本概念有以下几个：

• 选择算子：把当前群体中的个体$x_i$按与适应值$f(x_i)$成比例的概率$\frac{f_{x_i}}{\sum f_{x_i}}$进行筛选淘汰。选择算子提高了群体的平均适应值，低适应值的个体就会被淘汰，高适应值的个体则能被保留。
• 交叉算子：在种群中随机选择两个个体，交换它们染色体部分编码，产生两个新的子个体，既与父个体不同，但又包含父个体的大部分遗传信息。
• 变异算子：按某一极小概率随机改变染色体上的某个基因，从而增加群体的多样性。

进化算法解决问题的方法论：以基因方式编码，将问题转化为遗传算法问题；不断进化，直到达到预期目标。进化计算要求种群具有多样性，从中选择最好的基因，结果基本稳定之后，等发生突变后，产生多样性，再快速达到最高适应度。突变概率提高会使进化过程加快，但是会产生不稳定，进化过程波动较大。此外，可以增加种群的规模，产生多样性。

（四）基因重组与基因突变

交叉运算可分为以下几种情况。

1. 单点交叉

单点交叉是一种比较简单的交叉方式，它在两个个体的编码串中随机指定一个交叉点，交换对应的部分染色体，生成两个新的个体。例如，对大小为m的种群进行单点交叉配对，首先产生m/2（取整）组相互配对的个体，对每一组配对个体随机选择一个基因点作为交叉点。最后依照设定的某一交叉概率在交叉点处相互交换部分染色体编码串，即可完成两个新个体的生成。

2. 两点交叉和多点交叉

两点交叉是在编码串中随机设置两个交叉点，然后交换两个交叉点之间的染色体。例如1|10|10和1|01|01交换后得到1|01|10和1|10|01，“|”表示交换点。

由单点交叉与两点交叉可以很容易联想到多点交叉，即在个体的染色体编码串中随机设置多个交叉点，然后交换部分编码串。在实际的遗传算法实践中，一般不使用多点交叉方法，因为它可能破坏原有较理想的解。随着交叉点的增多，个体的编码结构被破坏的可能性会增大，就难以保持遗传基因的稳定性，从而影响遗传算法的效率。

3. 均匀交叉

均匀交叉是指两个配对个体生成新个体的过程中，基因编码串中每个基因位都以某一固定概率进行交换。均匀交叉可看成多点交叉的一种形式，在实际运算中，为了避免对编码结构的破坏，可设置规则来确保父类基因位的继承。

例如，随机产生一个与个体编码串长度相等的规则串$g_1，g_2，\dots ，g_n$，父代个体分别用$A、B$表示，当$g_i（i=1，2，\dots ，n）$为0时，子代 $A\prime$ 在第 i 位的基因值继承A对应值，$B\prime$在第i位的基因值继承B对应基因值，当gi为1时，则取相反情况。

4. 算术交叉

算术交叉是指两个个体通过线性组合产生两个新的子代个体。采用这种交叉方式的遗传算法，通常采用浮点数编码染色体。

例如，在$x_A、x_B$两个染色体之间进行配对，经过交叉运算后两个子代应为：

∂可以取一个常数，也可以选择一个由参数决定的变量。

5. 基因突变

（1）二进制编码

基因突变（Mutation）是染色体编码的某一位上基因的改变。基因突变使一个基因变成它的等位基因，并且通常会引起一定的表现型变化。在二进制编码中，按照一定概率将基因串上的0、1数字取反。例如下面的二进制编码：
101101001011001
经过基因突变后，可能变成新的编码：
001101011011001

（2）浮点型编码

浮点型编码的基因突变过程是对编码数值的增减，一般对原浮点数随机增加或者减少较小的数值。例如在突变之前的浮点数串如下：
2.3，5.6，6.2，8.0，6.3
经过基因变异后，可能得到如下的浮点数串：
2.4，5.5，6.1，7.8，6.5

遗传算法的一般步骤如下：

1. 随机产生一组初始个体构成初始种群，并根据适应度函数评价个体的适应值；
2. 判断算法是否满足某一指标（如收敛），若满足则停止并输出结果；
3. 根据适应值大小通过某一方式进行选择操作；
4. 对两两配对的个体按交叉概率执行交叉操作；
5. 按变异概率对个体中的基因执行变异操作；
6. 返回步骤 2 循环执行。

（五）遗传算法实现技术

1.编码

编码是为了建立个体特征和基因之间的映射关系，常用的编码方法有以下几种。

（1）二进制编码

二进制编码是遗传算法中最常用的编码方式，它使用二进制数字0、1表示染色体的基因信息，只要染色体足够长，就能描述个体的全部特征。二进制染色体示例如下：
010010011011011110111110
采用二进制编码，其编码、解码操作较为简单易懂，相对应的交叉变异等操作易于实现，但是，当个体特征比较复杂的时候，对应的编码会很复杂，相应的解码过程也将过分繁复，为降低算法的复杂性、提高运算效率，可采用浮点数编码的方式。

二进制编码的另一缺点是相临数字的二进制编码在二进制位上的区别可能会比较大，导致遗传算法的局部搜索能力不强。

（2）格雷码方法

格雷码编码是二进制编码的一种变形，是指连续两个整数所对应的编码值之间只有一个码位是不同的。这一特点解决了二进制编码中的相临数字的距离较远问题，增强了遗传算法的局部搜索能力。二进制、十进制与格雷码编码的对应关系如表所示。
####（3）浮点编码法
对于一些多维、高精度要求的连续函数优化问题，使用二进制编码来表示染色体信息会使编码冗长，不利于算法效率的提高。浮点数编码方式采用浮点数来表示个体的每个基因值，这种编码方式需要限制基因值的范围，保证基因值在给定的区间内，并且经过遗传算法中的交叉、变异等操作后，还要保证运算结果所产生的新个体的基因值也在这个区间范围内。

例如，某条染色体的编码如下：
1.2 – 3.3 – 2.0 –5.4 – 2.7 – 4.3
与前两种编码相比，浮点数编码可表示的数值范围较大，并且精度较高，支持较大的搜索空间，同时也改善了遗传算法的计算复杂性，适用于处理多极值函数的优化。

（4）符号编码法

符号编码法是指染色体编码串中的基因值可能涉及符号集（如｛A,B,C…｝）的字符，使用符号编码，便于编码有意义的基因值。这种编辑方法需要认真设计交叉、变异等遗传运算，以满足问题的各种约束，从而提高算法的搜索性能。

2. 群体的规模

规模较大的群体一般对应的个体多样性较高，可以避免算法陷入局部最优解。但增大群体规模的同时也会增加计算复杂度，降低算法效率。群体的规模选择过小会使搜索空间分布范围不足，因而搜索有可能停止在一个次优解。

群体规模与个体编码的长度相关，在实际应用中，个体编码长度越长，所需要的群体规模就要越大。群体规模并不是固定不变的，例如经过算法多次进化之后，得到的解仍没有达到优化目标，就说明现在的种群规模不足，种群多样性太少，需要对群体规模进行扩大；若结果的改进效果明显，则可以减少群体的规模以提高运算效率。

初始群体的选取采用随机的方法产生，实现所有状态的遍历，使最优解在遗传算法的进化中最终得以生存。也可采取启发式方法选取更加优良的群体。

在群体初始化的过程中，通常会产生一些竞争力较强的超常个体，对选择过程产生影响，使算法无法取得全局最优解，所以一般在初始化时生成比目标群体数量更多的个体，然后经过排序将超常个体淘汰，提高算法的稳定性。

3. 选择策略

对群体中个体的选择最能体现“适者生存”的自然选择法则，通过选择函数，从群体中选择优胜的个体，淘汰不满足目标条件的个体。选择合适的淘汰策略是遗传算法的关键，选择策略定义了在自然选择中的“公平”规则，通过适应函数进行量化。常见的策略有以下几类。

（1）基于适应值比例的策略

以个体的适应值作为选择依据，值越低越容易被淘汰，代表算法是轮盘赌及其改进算法。

（2）基于排名的策略

根据个体的适应度在整个群体中的排名来确定被选择的概率。将群体中的m个个体按适应值从小到大排列，记为1，2，…，m，选择概率$p_i=\frac{2i}{m(m+1)}$，1≤i≤m，这一策略在种群规模较小的情况下不会过快丧失种群多样性，从而避免过早收敛于局部最优解。

（3）基于局部竞争机制的策略

在群体中随机选择k个个体进行比较，其中适应度最好的个体被选择，以局部选择法、联赛选择法等为代表。

4. 适应度及选择函数

适应度函数（fitness function）用于计算群体中每个个体是否满足选择条件，一般是一个实值函数对个体进行评价。适应度函数值越大的个体，越满足于选择条件，即靠近最优解。由于适应度函数要比较排序并计算选择概率。因此，对于适应度函数，针对输入可计算出能加以比较的非负结果。适应度评估是选择操作的依据，适应度函数设计直接影响到遗传算法的性能。

当优化目标是求函数最大值，并且目标函数总取正值时，可以直接设定个体的适应度函数F(x)就等于相应的目标函数值f(x)。当求目标函数最小值的优化问题，则对目标函数值取反，即F(x)=-f(x)。

选择函数（selection）按照适应度个体进行淘汰，适应度高的个体被遗传到下一代种群中的概率就大。选择算子是一种选择方法，从父代中选择满足条件的个体遗传到下一代。常用的选择方法如下。

（1）轮盘赌（Roulette Wheel Selection）选择法

假设种群数目m，某个个体的适应度为$f_i$，则其被选中的概率为：

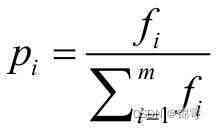
例如，有5条染色体所对应的适应度评分分别为：7、6、12、11、9，则累计总适应度为：

则各个个体被选中的概率分别为：

这个轮盘是按照各个个体的适应度比例进行分块的。类似于转动轮盘，轮盘停下来的时候，指针会随机地指向某一个个体所代表的区域，就相当于选中了该个体。

（2）随机遍历抽样法

随机遍历抽样法是对轮盘赌选择法的一种改进，只要进行一次轮盘旋转就可确定整个种群。假设种群规模为m，采用均匀分布的m个旋转指针，其中第一个指针的位置为［0，1/m］内的随机数，其他个体按照等距指针所指的位置进行选择。

（3）局部选择法

在局部选择法中，每个个体处于一个局部邻集中，个体仅与其临近的个体产生交叉。其中，邻集的定义与种群的分布结构相关，邻集可被当作潜在的交配伙伴。

（4）最佳个体保存方法

该方法是指群体中适应度最高的个体不对其进行配对交叉，而是直接复制到下一代中。此种选择又称为复制。此方法能使进化过程中某一代的最优解不被交叉和变异破坏，但可能会急速增加局部最优个体的基因而导致陷入局部最优解。该方法的全局搜索能力差，需要与其他选择方法结合使用。

（5）排序选择法

排序选择法是根据个体适应值的大小对其进行排序，按照顺序的不同采用不同的概率对个体进行选择。目标是使被选中的个体不要过于集中在高适应值个体，从而提高种群的多样性。

（6）联赛选择方法

该方法的操作思想是从群体中任意选择一定数目的个体（一般选2个），其中适应度最高的个体保存到下一代。这个过程反复执行，直到保存到后代的个体数达到预先设定的数目为止。

5. 变异算子

变异算子能使个体按一定概率发生变异，产生新的遗传基因，有助于增加种群多样性，是提高全局最优搜索能力的有效步骤，也是保持群体差异、防止过早出现收敛的重要手段。在遗传算法中，交叉和变异这对相互配合又相互竞争的操作，使算法具备兼顾全局和局部的均衡搜索能力。

通过选择、交叉、变异得到新的群体替换率与交叉概率$p_c$和变异概率$p_m$相关，替换率较低的情况下，每代种群更新较慢，使得搜索的范围扩展较慢，但能够较大程度的保留现有基因。过高替换率也是不可取的，会过滤掉当前的最优解。可以采用一种保留策略，使上一代的当前最优解强行遗传到下一代。

遗传算法的优越性如下:

1. 能够普遍适用于数值求解问题。对目标函数要求低，总能以极大的概率找到全局最优解。
2. 在求解很多组合优化问题时，不需要对问题有非常深入的理解，在确定问题的决策变量编码后，其计算过程是比较简单的，且可较快地得到一个满意解。
3. 与其他启发式算法有较好的兼容性，容易结合形成性能更优的问题求解方法。

遗传算法在解决优化问题过程中可以很快找到较优的解，此外还具有以下特点:
4. 有可能收敛于局部最优，特别是在适应度函数（Fitness Function）选择不当的情况下，适应度函数对于算法的速度和效率很重要。
5. 如果初始种群数量过多，算法的计算量比较大，会耗时较长；反之，算法很可能无法取得最优解，所以初始种群的数量很关键。
6. 遗传算法不能解决那些很难定义适应度函数来表征个体好坏的问题，否则会使得算法的进化失去方向。
7. 可以调整个体数目、交叉率和变异率使遗传计算法更好更快收敛。其中，太大的变异率会导致丢失最优解，而过小的变异率会导致算法过早的收敛于局部最优点。

(六）遗传算法实例

下面举例说明遗传算法的应用。

【例1】应用遗传算法解决旅行商（Travelling Salesman Problem，TSP）问题：给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。

基于遗传算法求解旅行商问题的研究有很多。旅行商问题用于评价不同的遗传操作和选择机制的性能，主要有以下原因。

1. 旅行商问题是一个易于描述却难以处理的问题，在可计算理论中有着重要的理论价值。
2. 旅行商问题是诸多领域内出现的多种复杂问题的集中概括和简化形式，有一定的实际应用价值。

设：

式中 z 为经过所有城市的路径总长度，$d_{ij}$为城市 i 和 j 之间的距离。

1. 编码

（1）路径编码

例如：1623457 表示1→6→2→3→4→5→7→1，其中1～7表示城市的代号。

（2）顺序编码

将所有城市按顺序构成一个顺序表，对于一个旅程，可以依据行程经过的顺序处理每个城市，每个城市在顺序表中的顺序就是一个遗传因子，每次处理完一个城市，从顺序表中去掉该城市。处理完所有城市后，将每个城市的遗传因子表示连接起来，即成为这个旅程的基因编码。

例如顺序表C : 1 2 3 4 5 6 7 8 9，一个旅程为1→2→4→3→7→6→9→8→5→1，则顺序编码为1:1 1 2 1 3 2 3 2 1。

（3）布尔矩阵编码

布尔矩阵编码采用非向量表示方法，一个旅程定义为一个优先权布尔矩阵$M$，当且仅当城市 i 排在城市 j 之前时矩阵元素$m_{ij}=1$。如旅程为7→2→1→8→3→4→5→9→6→7，则$M$中第7行中除第7列外均为1。矩阵$M$具有如下三个性质：

• 矩阵中1的数目为$\frac{n(n-1)}{2}$；
• $m_{ij}=0，i=1～n$；
• 若$m_{ij}=1$，且$m_{jk}=1$，则$m_{ik}=1$。

2. 适应度函数

适应度函数值为回路长度的倒数。

3. 基于遗传算法求解

例如两个父个体A：（1 2 3 4 5 6 7 8 9）和B：（4 1 2 8 7 6 9 3 5），对两个父代矩阵中位进行交叉运算（A中的4 5 6与B中的8 7 6交换），得到两个新个体：

交叉后计算新个体的适应度值，利用上面的选择策略之一，保留适应度稍大的个体，再经过变异操作，如此往复，直至旅程的总长度不再减少。

二、蚁群算法

蚁群算法（Ant Colony Optimization，ACO），又称蚂蚁算法，来源于蚂蚁寻找食物的过程。自然界中蚂蚁的很多行为由“信息素”这一化学物质所调控。通过科学观察发现，蚂蚁总能发现一条从蚁巢到食物源的最短路径。蚂蚁能够在经过的路途中留下“信息素”作为标记，以此来指导自己的活动轨迹。蚂蚁倾向于选择那些“信息素”浓度高的路径，某一路径上走过的蚂蚁越多，遗留下的“信息素”越多，被选中的概率就越大，最终形成最短路径。蚁群算法具有许多优良性质，已应用在多个场合。

蚁群算法对蚂蚁行为进行抽象，采用“图”来描述蚂蚁的活动范围，将蚂蚁的行动轨迹抽象成图中的边，蚂蚁的移动过程则相当于按照一定概率的节点之间的转移，从初始节点到目标节点。

假设M表示节点数量，m表示蚂蚁数量。m的数量若过大易导致路径上信息素差距不够明显，m数量过小易使未检索的路径信息素减小到0，这样可能找不到全局最优解。一般来说，蚂蚁数设定为节点数的1.5倍较稳妥。

1.信息素因子

信息素因子表示蚂蚁在移动过程中所积累的信息素浓度，类似于图中每一条边的权值。其中，权值较大的路径被蚂蚁选择的概率也大，降低了探索路径的随机性；权值过小易使搜索过早陷入局部最优。一般来说，信息素因子选择[1，4]区间，性能较好。

2.启发因子

启发因子度量的是启发式信息在蚁群搜索过程中的重要程度，其值越大，路径选择的随机性会越弱，蚁群倾向于选择之前走过的路径，这时算法的收敛速度会加快，但容易陷入局部最优；反之，随机性越强，算法很难收敛，找不到最优解。

3.信息素挥发因子

信息素会随时间推移不断挥发，而信息素挥发因子表示信息素的消失水平，它直接关系到蚁群算法的全局搜索能力和收敛速度。一般来说，当信息素挥发因子位于属于[0.2，0.5]时，综合性能较好。

4.信息素常数

信息素常数的作用是利用有向图上的“信息素”，使算法在正反馈机制作用下逐步演化，直到搜索到全局最优解。其值越大，表示蚂蚁在已遍历路径上的信息素积累越快，有助于快速收敛。一般来说，当值属于[10，1000]时，综合性能较好。

5.算法步骤

以TSP问题为例，算法的基本步骤如下。

1. 步骤1：对问题进行定义，即寻找遍历图中所有节点的最短路径，并预处理数据，将每个节点的坐标信息转换为图存储的节点距离矩阵。然后对蚁群数量、信息素因子、启发因子、信息素挥发因子、信息素常数等参数进行初始化。
2. 步骤2：将蚂蚁随机放置于不同的出发节点，并通过计算来指定蚂蚁的下一访问节点，直至遍历完所有节点。
3. 步骤3：每次迭代完成之后，计算所有蚂蚁经过的路线，更新每条路径上的信息素值，路径越短，信息素的浓度越高，从而得到当前迭代的最优解。
4. 步骤4：判断是否达到停止条件（迭代次数或最优条件），若否，则进入步骤2；否则结束迭代。
5. 步骤5：输出全局最优结果。

三、蜂群算法

自然界中蜜蜂能够适应环境变化以极高的效率采集花蜜。尽管单一的蜜蜂完成的工作简单，但蜜蜂群体能够通过一系列信息交流方式，如摇摆舞、气味等，自然高效地完成采蜜授粉工作。蜜蜂采蜜活动过程大致如下。

1. 第一只发现蜜源的蜜蜂以摇摆舞的方式发出信号；
2. 其他蜜蜂接收到信号，确定蜜源位置信息；
3. 选择前往蜜源或在附近寻找新的蜜源。

蜜蜂通过这样反复的信息交流，使得蜂群能够找到较多的蜜源，达到群体最优。人工蜂群算法则是模拟蜜蜂的采蜜过程，通过个体的局部最优行为，使得群体的最优值突显出来，其本质是对遗传算法的改进。

1. 人工蜂群算法的描述

（1）引入代表解空间中的可能解的蜜源，并初始化“适应度”来度量蜜源，用于决定蜜蜂是否选择前往采蜜。

（2）引入三种蜜蜂。

1. 采蜜蜂：与蜜源相关联，采蜜蜂对应其正在采蜜的蜜源，同时测量蜜源适应度，并通过摇摆舞的方式将蜜源信息发布出去；采蜜蜂总能记住所经过的最佳采蜜点，并能够凭记忆在经过的路径区域搜索；
2. 观察蜂：检测采蜜蜂发出的信息，并根据这些信息判断蜜源的适应度，选择前往蜜源或继续等待新的信息，适应度越大的蜜源被选择的可能性越高；
3. 侦察蜂：随机搜索新的蜜源。

（3）在循环过程中，每个蜜源设定只有一个采蜜蜂，整个蜂群中采蜜蜂和观察蜂的数量可以相等，当设定的蜜源（适应度）被耗尽时，采蜜蜂将转变为侦察蜂，寻找新的食物源，三种蜜蜂在不同的条件下可以相互转换。

2. 人工蜂群算法基本实现步骤

（1）对蜜蜂种群进行初始化。在初始时刻，蜜蜂没有获得采蜜的记忆，所有蜜蜂都是侦察蜂随机搜索蜜源，并根据蜜源情况判读对应蜜源的适应度f。

设定蜜蜂总数为m，其中采蜜蜂和观察蜂各为$\frac{m}{2}$。

设定最大迭代次数max。

设定蜜源的最大限制搜索次数lim，搜索lim次后，若没有新的蜜源加入，则采蜜蜂、观察蜂转化为侦察蜂。

（2）按照适应度$f$对所有蜜源排序，适应度较高的蜜蜂作为采蜜蜂，较低的为观察蜂。观察蜂根据采蜜蜂的舞蹈信息判断蜜源的花蜜量，适应度越高的蜜源吸引的观察蜂越多。蜜源被观察蜂选择的概率为：

其中，$f_i$是蜜源i的适应度值，正比于该蜜源的花蜜量，n为蜜源总数量，与采蜜蜂的数量相等。

（3）每只蜜蜂在蜜源采蜜的同时，搜索附近蜜源并计算其适应度，若新蜜源的适应度高于原蜜源，则以新蜜源取代原蜜源。

新蜜源的位置选择如下：

$L_{new}=L_i+rand(L_i-L_j)$

由公式可知，rand()是指在[-1，1]之间取随机数，当$L_i$和$L_j$两个参数相差较小时，在Li这个位置的波动就较小，在搜索区域快达到最优解时，蜜蜂搜寻新的蜜源所移动的距离较小。

（4）若采蜜蜂、观察蜂对某一蜜源的搜索次数达到lim值，仍没有发现更高适应度的蜜源，则放弃该蜜源并转化为侦察蜂，随机产生一个新的蜜源；

（5）记录所有蜜蜂找到的最优蜜源，返回步骤2。若迭代次数达到max，则输出全局最优解。

3. 蜂群算法应用案例

蜂群算法广泛应用于图像处理、无线通信、组合优化和控制工程等领域，能够较快探索到优化问题的最优解。

采蜜行为和优化问题的对应关系，如表所示。

【例2】蜂群算法在车辆路径规划的应用。

假设有K辆车的容量分别为$q_k（k\in ｛1，2，\dots ，K｝）$；需要完成L个站点的配送任务，其编号分别为1，2，…，L，每个站点需要配送的货物量为$g_i（i\in ｛1，2，\dots ，L｝$，且$max｛g_i｝\le max{q}_k$；$c_{ij}$为站点 i 至站点 j 的距离，$x_{ijk}$表示编号 k 的配送车辆从 i 站点前往 j 站点，一辆配送车辆可同时服务于多个站点，但同一站点的货物只能由一辆车进行配送；车辆路径的规划也是一个NP hard问题，其优化目标是整体配送路径长度F为最短：

需要满足如下约束：

当 i 站点的运输任务由配送车 k 执行任务时，$y_{ki}$的值为1，否则为0。当配送车 k 执行从站点 i 到站点 j 配送任务时，$x_{ijk}$值为1，否则为0。同时，每辆配送车所承担的总的货运量不能超过自己的最大载重量且每个站点仅有一辆配送车量负责为其提供服务。

将蜂群算法应用于车辆路径规划，采用一种基于车辆位置次序和车辆位置取整操作的三维编码方法（见表）。在这种编码方式中，第一维采用自然整数1，2，…，L表示配送范围内所有站点编号，按递增顺序排列；第二维$e_{ij}$表示分配给各个客户点的车辆编号，$e_{ij}\in [1，K+1)$；第三维$o_{ij}$用于映射车辆的行驶顺序。

对以上编码进行解码，首先将第二维的值$e_{ij}$向下取整，即可得到分配给客户点j的车辆编号 k。对于分配给同一辆车 k 的客户点，按照第三维的值$o_{ij}$，从小到大进行排列，即可得到路径点。

假设仅有2辆配送车需要完成6个站点的配送任务，其第 i 个食物源的编码如表所示。

在经过对第二维的值进行向下取整后，编码转换如表所示。

然后将各个站点按第二维的值分组，按照第三维的值从小到大排列，可完成路径解码。示例编码代表的路径为1号车的路径为1→3→5→4，2号车路径为6→2。

在寻找候选食物源时，算法从当前食物源中随机选取一个站点，对其$e_{ij}$和$o_{ij}$分别进行邻域搜索计算，生成候选食物源。

在蜂群算法中，采蜜蜂具有记忆功能，能够根据上一轮循环的最优解进行邻域搜索，使得路径规划结果更加合理，将相互靠近的站点，按距离配送点远近的顺序，安排同一辆车进行配送。观察蜂在采蜜蜂所获得的食物源的基础上，按照适应度为各个食物源进行局部搜索，保证富源有更多的机会进行局部搜索。而在算法陷入停滞到一定程度时，侦察蜂可以帮助整个解群跳出局部最优，保持整个解群的多样性。

---

参考资料：《机器学习》–赵卫龙