SNN识别手写数字—MNIST数据集
提示:参考论文:
“Unsupervised learning of digit recognition using spike-timing-dependent plasticity”
文章目录
-
- 一、前言
- 二、snn的训练过程
-
- 2.1snn网络的搭建
- 2.2 snn网络的训练
- 2.3 snn 训练结果保存
- 三、snn的测试过程
- 四、snn识别的准确率
一、前言
1、数据集
(1)MNIST数据集介绍
MINST数据集格式,官网给的数据集合并不是原始的图像数据格式,而是编码后的二进制格式:
head+data模式: 前16个字节分为4个整型数据,每个4字节,分别代表:数据信息des、图像数量(img_num),图像行数(row)、图像列数(col),之后的数据全部为像素,每row*col个像素构成一张图,每个色素的值为(0-255)。
(2)训练数据集大小:结合服务器性能,这里采用20000条数据训练。原文中是采用60000条、60000*3……(对服务器的性能要求较高)
(3)测试数据集大小:采用10000条MNIST数据进行测试
2、神经元模型——LIF模型(Leaky Intergrate and fires model)
LIF模型任务:找到膜电势随时间以及外界输入的变化情况。(具体的模型网上由很多,此处介绍简单的概念。)
-
Leaky
泄露,表示如果神经元的输入只有一个,且不足以令膜电位超过阈值,膜电位会自动发生泄露逐渐回落到静息状态; -
Integrate
积分,表示神经元会接收所有与该神经元相连的轴突末端(上一个神经元)到来的脉冲 -
Fire
激发,表示当膜电位超过阈值,神经元会发送脉冲
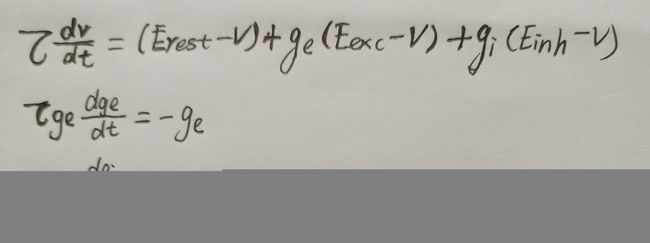
Erest是静息膜电位
Eexc和Einh是兴奋性和抑制性突触的平衡电位
ge和gi是兴奋性和抑制性突触的电导
3、突触模型(权重修改rule)——pair-based STDP
参考链接
1)经典STDP模型
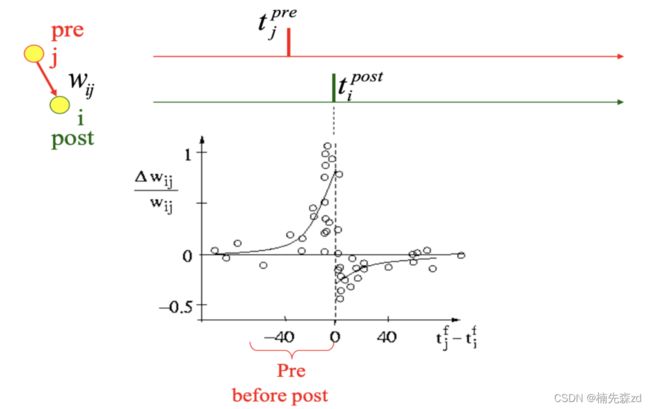
来自突触前神经元 j 的突触权重变化Δω依赖于突触前脉冲的到达和突触后脉冲的相对时序。W表示STDP函数。在成对的突触前后脉冲上按照刺激规则,总权重变化Δωj 是:
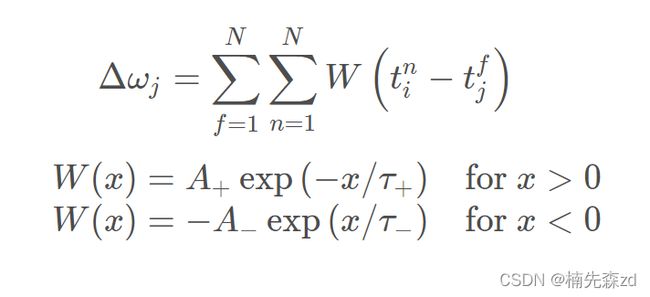
注意:传统的STDP不得不将所有的脉冲对相加,在生物上,也是不可实现的,因为神经网络不可能记忆之前的脉冲时间。相反,还存在许多高效和生物相似性高的方法可以实现同样的效果。如下面所示,通过使用迹的方式实现权重的更新。
2)online-STDP
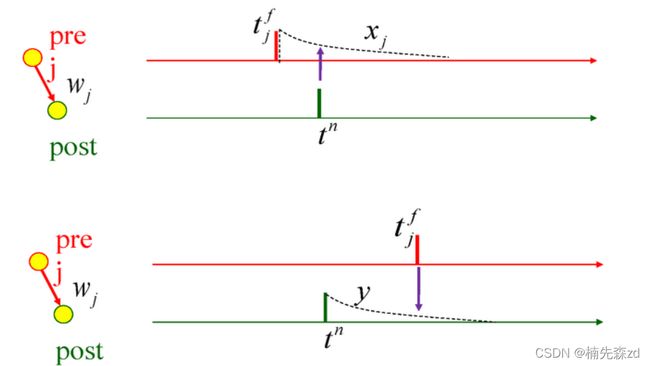
xj是突触前脉冲到达后留下的轨迹,这条轨迹在脉冲到达时为a+(x),在没有脉冲时按指数衰减;
y是突触后脉冲到达后留下的轨迹,这条轨迹峰值在脉冲到达时为a_ ( y ) ;
t_fj是突触前脉冲到达的时间;
t_n是突触后脉冲到达的时间;

上图的公式3描述了突触权重的变化:
在突触后发射脉冲时权重增加,这个量取决于先前突触前脉冲留下的轨迹;
在突触前发射脉冲时权重减少,这个量取决于先前突触后脉冲留下的轨迹
注意:该方法与经典的STDP在更新上略有区别,经典的STDP每当脉冲到来时计算其影响,online方式通过使用迹的方式,将脉冲到来看作是一个开关,之前的脉冲的影响全在迹中保存。
3)因此在代码中我们采用online-STDP(利用brain平台):

4、网络结构
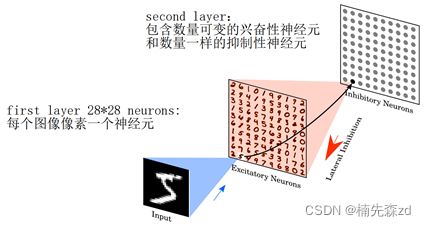

1)Ae和Ai之间生成的权重矩阵是固定的,不需要学习更新:
Ae->Ai权重一 一对应连接:权重矩阵(400,3)
Ai->Ae权重全连接(主对角线不可以对应连接):权重矩阵(160000,3)

2)Xe->Ae权重全连接(这些权重要进行归一化):权重矩阵(313600,3)
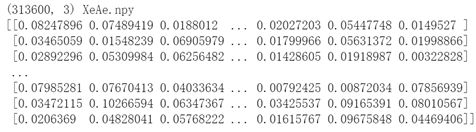
说明:(400,3)、(160000,3)、(313600,3)中的:
横坐标‘400’、‘160000’、‘313600’表示突触个数,即前后神经元组之间的连接个数;
纵坐标‘3’不表示输出矩阵的维度,表示从npy文件中读出的列的维度,三列分别表示(location_ i,location_ j,weight_data);
思考一个问题:Ai->Ae、Ae->Ai、Xe->Ae的权重矩阵在训练过程和测试过程中分别从何而来(如何获得)?下面有解答。
5、云服务器配置
CPU 1核
内存 4GB
高性能云硬盘 50GB 、
带宽 1Mbps
操作系统 Ubuntu Server 18.04.1 LTS 64位
6、训练结果
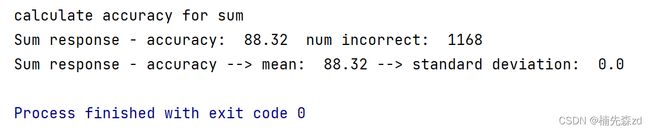
20000条数据训练模型,再用不同的10000条数据测试
准确率为:88.32%,即10000个数字识别错了1168个
二、snn的训练过程
2.1snn网络的搭建
1.神经元组neuron_groups{} 这里先不考虑输入神经元组!
1)定义神经元组:
neuron_groups[‘e’]= b2.NeuronGroup(400,neuron_eqs_e, threshold= , refractory=, reset=, method=‘euler’)、
neuron_groups[‘i’] 、neuron_groups[‘Ae’] 、neuron_groups[‘Ai’]同理即可。
2)神经元参数配置:
neuron_groups[‘Ae’].v = -105* b2.mV
neuron_groups[‘Ai’].v = -100*b2.mV
neuron_groups[‘e’].theta = np.ones(400)20.0b2.mV
注:膜电位阈值 theta 在训练的时候是直接读取
2.突触连接AiAe/AeAi(有了神经元组即可创建组之间的连接关系)
1)AiAe/AeAi之间创建循环连接:
connections[connName] = b2.Synapses(neuron_groups[‘Ae’], neuron_groups[‘Ai’],model=, on_pre=, on_post=);
connections[connName] = b2.Synapses(neuron_groups[‘Ai’], neuron_groups[‘Ae’],model=, on_pre=, on_post=)
2)权重赋值:
connections[connName].w = weightMatrix[connections[connName].i, connections[connName].j]
weightMatrix = get_matrix_from_file(weight_path + ‘…/random/’ + connName + ‘’ + ‘.npy’)
#可以看出,训练时的权重是代码直接生成的,相当于直接赋初值。
3.对神经元组A创建监视器monitors
spike_counters[‘Ae’] = b2.SpikeMonitor(neuron_groups[‘Ae’])
#spike_counters表示组中每个神经元被激发脉冲的数量,这个记录值后面会频繁用到,较为重要
spike_monitors[‘Ae’] = b2.SpikeMonitor(neuron_groups[‘Ae’])
spike_monitors[‘Ai’] = b2.SpikeMonitor(neuron_groups[‘Ai’])
#spike_monitors.t和spike_monitors.i 分别表示神经元激发脉冲的时间和神经元序号index
rate_monitors[‘Ae’] = b2.PopulationRateMonitor(neuron_groups[‘Ae’]) rate_monitors[‘Ai’] = b2.PopulationRateMonitor(neuron_groups[‘Ai’])
#PopulationRateMonitor:监视源时钟每个时间步的瞬时触发率。
接下来我们考虑输入神经元组:
4.输入神经元组input_groups{}
1)输入神经元组定义
input_groups[‘Xe’] = b2.PoissonGroup(784, 0*Hz)
#生成泊松分布的输入脉冲
2)对输入神经元组Xe创建监视器
rate_monitors[‘Xe’] = b2.PopulationRateMonitor(input_groups[‘Xe’])
spike_monitors[‘Xe’] = b2.SpikeMonitor(input_groups[‘Xe’])
3)X和A之间的突触连接
创建连接:
connections[XeAe] = b2.Synapses(input_groups[‘Xe’], neuron_groups[‘Ae’],
model=, on_pre=, on_post=)
连接参数配置:
connections[XeAe].delay = ‘minDelay + rand() * deltaDelay’
connections[XeAe].w = weightMatrix[XeAe.i, XeAe.j]
其中:
weightMatrix = get_matrix_from_file(./random/XeAe20000.npy)
weightMatrix是(784×400,3)即(313600,3)
5.组建网络
这里是是Brain2里Network的用法,将上述定义的神经元组(neuron_groups和input_groups)、突触连接(connections),以及监听器(rate_monitors、spike_monitors、spike_counters)等加入网络net中:
net = Network()
for obj_list in [neuron_groups, input_groups, connections, rate_monitors,
spike_monitors, spike_counters]:
for key in obj_list:
net.add(obj_list[key])
注:到这里,我们搭建好了整个网络的框架(神经元组,组之间的连接方式和连接权重),此外我们发现在训练snn的过程中Xe,Ae,Ai之间的权重都是代码直接生成的。
2.2 snn网络的训练
先列出代码,再进行分析:
assignments = np.zeros(n_e)
input_groups[name+'e'].rates = 0 * Hz #将输入神经元的脉冲激发率置0
net.run(0*second)
while j < (int(10000)): #num_examples=6,0000 1/3的数据拿来训练
if test_mode:
if use_testing_set:
spike_rates = testing['x'][j%10000,:,:].reshape((n_input)) / 8. * input_intensity
else:
spike_rates = training['x'][j%20000,:,:].reshape((n_input)) / 8. * input_intensity
else: #针对X和A之间的权重连接,且这里的权重进行正则化其实指的是,将权重值范围缩小到0-1之间,应该说是归一化
normalize_weights() #L2正则化也是权重衰减,可以叫激活函数变得更加线性,抑制过拟合
spike_rates = training['x'][j%20000,:,:].reshape((n_input)) / 8. * input_intensity #spike_rates是一个临时变量,表示的是放电的速率:取出每一个样本的28*28的像素值,然后重新排列为一个784的列表,再除以4,将255限制在255/4的范围内。
input_groups['Xe'].rates = spike_rates * Hz #input_groups是输入的28*28的神经元,长度是784的列表。
if j % 10000 == 0:
print ('run number:', j+1, 'of', int(num_examples))
net.run(single_example_time, report='text') #输入向网络呈现350ms,输入以泊松分布的脉冲序列的形式呈现
# assignments的形状是(400,),表示400个神经元分别被识别为数字j(j=0~9),即每一个神经元都有自己的所属类别!
if j % update_interval == 0 and j > 0: #update_interval=10000
assignments = get_new_assignments(result_monitor[:], input_numbers[j-update_interval : j])
if j % weight_update_interval == 0 and not test_mode: #weight_update_interval=100
update_2d_input_weights(input_weight_monitor, fig_weights) #更新了 input_weight_monitor
if j % save_connections_interval == 0 and j > 0 and not test_mode: #save_connections_interval=10000
save_connections(str(j))
save_theta(str(j))
# spike_counters['Ae'].count 表示Ae层的神经元激发的脉冲数量,具有累加性!
current_spike_count = np.asarray(spike_counters['Ae'].count[:]) - previous_spike_count #累加性保证当前神经元激发的脉冲数为正
previous_spike_count = np.copy(spike_counters['Ae'].count[:])
if np.sum(current_spike_count) < 5:
input_intensity += 1
for i,name in enumerate(input_population_names):
input_groups[name+'e'].rates = 0 * Hz
net.run(resting_time)
else:
result_monitor[j%update_interval,:] = current_spike_count #将当前每个神经元激发脉冲的数量存到result_monitor中
if test_mode and use_testing_set:
input_numbers[j] = testing['y'][j%10000][0]
else:
input_numbers[j] = training['y'][j%20000][0]
outputNumbers[j,:] = get_recognized_number_ranking(assignments, result_monitor[j%update_interval,:])
# outputNumbers存放着每个样本最终分配到的类别,后面有用到么??
if j % 10000 == 0 and j > 0:
print ('runs done:', j, 'of', int(num_examples))
if j % update_interval == 0 and j > 0:
if do_plot_performance:
unused, performance = update_performance_plot(performance_monitor, performance, j, fig_performance)
print ('Classification performance', performance[:int(j/float(update_interval))+1])
for i,name in enumerate(input_population_names):
input_groups[name+'e'].rates = 0 * Hz
net.run(resting_time)
# 在每个image输入之前,需要延迟150ms,为了让神经元的变量衰减到静息状态
input_intensity = start_input_intensity
j += 1
1.得到 input neurons 的脉冲激发率 , 即input_groups[‘Xe’].rates
利用脉冲激发率 spike_rates 和像素强度pixel_value成正比的原则:
取一个数字样本的28*28个像素值,重新排列为长度为784的列表,再除以4(将像素强度转换为脉冲激发率)。
input_groups[‘Xe’].rates = spike_rates * Hz #input_groups是输入神经元
2.运行网络net.run()
有了输入、有了网络框架,就可以训练网络了(将输入向网络呈现350ms,输入以泊松分布的脉冲序列的形式呈现)。
思考一个问题:
在训练网络的过程中,神经元的膜电位,突触权重是怎样发生变化的?
即与neuron_groups, input_groups, connections, rate_monitors,spike_monitors, spike_counters等变量相关的参数是如何更新的?
答案应该是: net.run(350ms, report=‘text’) #run之后,网络中包含的神经元参数、突触参数、监控器的参数都会发生改变。如权重:connections[‘XeAe’].w和膜电位自适应阈值θ:neuron_groups[ ‘Ae’].theta都会进行更新。
3.更新参数
run之后,根据输入神经元激发的脉冲,可以得到Ae层神经元激发的脉冲数量( spike_counters[‘Ae’].count 和current_spike_count),进而更新其他的参数。
1)spike_counters[‘Ae’].count 和current_spike_count
区别1:
current_spike_count
=np.asarray(spike_counters[‘Ae’].count[:]) - previous_spike_count
区别2:
spike_counters[‘Ae’].count:
具有累加性,每个输入数字使得Ae层神经元激发的脉冲要进行累计
current_spike_count:
不具有累加性,当前输入数字使得Ae层神经元激发脉冲的数量,不考虑之前输入数字的影响。
2)result_monitor
result_monitor[0:20000 , : ] = current_spike_count
#result_monitor是20000行400列,存储着所有数字的current_spike_count
3)input_numbers
input_numbers[ j ] = training[‘y’] [j%20000] [0]
#input_numbers存储着所有数字的真实的标签。
4)assignments
assignments的shape是(400,) 代表着400个神经元的分类结果0-9。(即每一个神经元都有自己的所属类别!)
4.有了以上的这些参数,我们可以进一步分析以下函数的功能
1)get_recognized_number_ranking函数
每次循环都会执行的函数(分析详见代码注释);
outputNumbers[j,:] = get_recognized_number_ranking(assignments, current_spike_count)
函数功能: 输入一个数字样本,根据Ae层神经元在不同分类下的脉冲激发率对该样本类别进行判断(没有使用label)
输入参数: assignments、current_spike_count(图形化理解如下):

输出参数: outputNumbers存放着每个输入样本估计的类别
def get_recognized_number_ranking(assignments, spike_rates):
summed_rates = [0] * 10
num_assignments = [0] * 10
for i in range(10):
categoryi=(assignments == i)
'''categoryi是一个数组,里面是布尔值:神经元属于第i个分类用True表示,否则用False表示。方便后面的计数。'''
num_assignments[i] = len(np.where(categoryi)[0])
'''属于第i类的神经元的个数 or 值为true的个数'''
if num_assignments[i] > 0:
summed_rates[i] = np.sum(spike_rates[categoryi]) / num_assignments[i]
''''spike_rates[categoryi]是列表,里面是布尔值,第i类用true表示,否则用false表示。方便后面计数。'''
'''分子:第i类神经元总的脉冲激发数(np.sum(spike_rates[categoryi])是对第i类的神经元激发的脉冲数量进行求和)
分母:属于第i类的神经元的个数'''
return np.argsort(summed_rates)[::-1]
'''结果summed_rates分析:
第i类神经元总的脉冲激发数/属于第i类的神经元的个数
<=>表示单个神经元所激发的脉冲的个数(类似第i组的单个人的价值贡献量)。'''
#[::-1]的作用是倒序。np.argsort返回的是下标(概率从小到大进行排列的数字所对应的下标)
# 最终返回的是概率从大到小的概率所对应的元素下标。array([0, 9, 8, 7, 6, 5, 4, 3, 2, 1], dtype=int64)表示下标为0的元素是概率最大的那个。
2)get_new_assignments函数
每1w次循环执行1次的函数(分析详见代码注释);
assignments = get_new_assignments(result_monitor[:], input_numbers[j-10000: j])
函数功能: 更新Ae层400个神经元的类别
输入参数: 输入样本label、result_monitor(1w个输入样本对应的Ae层400个神经元脉冲激发数量)
输出参数:(1w个输入样本得到的)Ae层400个神经元分类
def get_new_assignments(result_monitor, input_numbers):
assignments = np.zeros(n_e)
input_nums = np.asarray(input_numbers) #input_numbers=(np.random.randint(10,size=10000))
# np.array与 np.asarray 功能是一样的,都是将输入转为矩阵格式。
maximum_rate = [0] * n_e
for j in range(10):
category=(input_nums == j)
# category是数组,里面是布尔值 。 如果input_nums == j,那么第j类=第category类,那么为 true,否则为 false
num_assignments = len(np.where(category)[0])
#num_assignments是: 第j类 输入样本个数,这里有10000个样本
if num_assignments > 0:
rate = np.sum(result_monitor[category], axis = 0) / num_assignments
''' 1.result_monitor[category]分析:result_monitor是数组,categor也是数组,最终挑选出为category类的数字,
形状由10000行400列变为——>num_assignments 行400列
2.np.sum()即将num_assignments行求和变为1行(axis = 0表示矩阵在竖列的方向上求和)
求和后就变为了1行400列的数组,每1列代表:这个神经元(在categor类别时)所激发的脉冲总数,方便后期去判断这个神经元属于哪个类别。
分子:(是多维数组) Ae层神经元激发脉冲的总和
分母:(是实数) 判断第j类数字的个数'''
for i in range(n_e):
if rate[i] > maximum_rate[i]:
maximum_rate[i] = rate[i]
assignments[i] = j
return assignments
图示直观理解(条件假设为理想状况,方便理解):
3)save_connections(str(j)) 和 save_theta(str(j))函数
函数功能: 保存权重、膜电位自适应阈值θ
#调用时,ending取值为样本数量j(如:1w,2w,3w……)
def save_connections(ending = ''):
print ('save connections')
for connName in save_conns:
conn = connections[connName]
connListSparse = list(zip(conn.i, conn.j, conn.w)) #参数分别为 Xe的索引,Ae索引,和XeAe之间的连接权重。
np.save(data_path + 'weights/' + connName + ending, connListSparse)
def save_theta(ending = ''):
print ('save theta')
for pop_name in population_names:
np.save(data_path + 'weights/theta_' + pop_name + ending, neuron_groups[pop_name + 'e'].theta)
思考一个问题:
保存的权重(connections[‘XeAe’].w)和θ值(neuron_groups[ ‘Ae’].theta)是怎样得到的?如何变化?答案其实在上面解释过,即net.run。
这里引用brain中的一段话进一步解释:
代码中,创建network对象,这是因为在循环中,只有运行了“run”,那所有的对象都会被运行,但是我们只想运行1次的话,那就需要用network去明确指定要包含哪些对象。这说明了如果不run,那么突触权重等参数都无法进行更新。
2.3 snn 训练结果保存
当所有的输入样本全部训练完成之后,
保存权重 list(zip(connections[‘XeAe’].i, connections[‘XeAe’].j, connections[‘XeAe’].w))到路径:‘./weights/XeAe’
保存theta值 neuron_groups[‘Ae’].theta到路径:‘./weights/theta_A’
方便snn测试的时候使用。
三、snn的测试过程
训练时:路径为random文件,使用的是random中由随机代码直接生成的权重和θ的npy文件。训练完成后,产生的文件有:
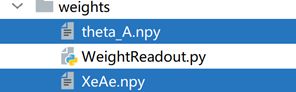
测试时,路径为weights文件,使用的便是上图中的权重和θ的npy文件。测试结束后,产生的文件有:
文件的含义:
inputNumbers10000.npy是input_numbers,输入样本的label;resultPopVecs10000.npy是result_monitor,Ae层400个神经元的脉冲激发率。
注:
1)测试的时候不需要保存权重和θ值;
2)但是无论训练还是测试,从Ae->Ai的权重矩阵用的都是randoom中XeAe/XeAi的权重文件
四、snn识别的准确率
主要利用get_recognized_number_ranking函数(上文中已经介绍,此处不在赘述),得到每个输入样本的预测值,进而与label进行比较,最终即可得到snn的准确率。


