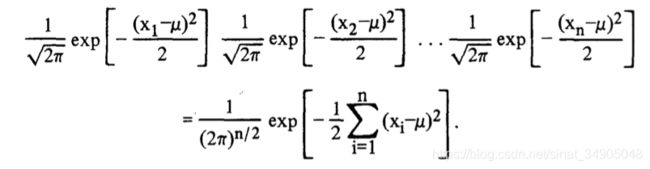故障树手册（Fault Tree handbook)（6）

第十章 概率与统计分析

1 概述

在这章中，我们将试图去描述和故障树相关的概率与统计概念中的基本元素。这些知识也是故障树量化的基础。在这方面基础好的读者可以直接跳过本章去阅读第十一章，在后边需要的时候再来回顾对应的内容。

我们现在先来讨论概率分布理论。我们首先会讲解二项分布，接着学习常规的分布原理，并重点学习一些在系统分析中常用到的特殊分布。然后我们将具备统计评估的基础知识。

我们的表示法或许不是最好的传统数学统计，我们的方法是一个作者在对工程学的学生和工程师统计课程的过程中所采用的改进后的方法。我们有时会为了更好更快的阐述概念而牺牲一些数学的严谨性。

2 二项分布

假设我们有四个相似的系统，这些系统都经过特定时间的测试。在测试的最后我们进一步的假设所有的测试结果我们都准确的以“成功”或“失败”进行了记录。如果成功的概率用p来表示（失败的概率就是1-p），那么在四次实验外的成功的概率是多少？

这个实验的结果集合可以用如下表示（下标表示第几次实验，S表示成功，F表示失败）：

$S_1{F}_2{S}_3{F}_4$表示“第一次沈工，第二次失败，第三次成功，第四次失败”。该结果的概率为$p\cdot (1-p)\cdot p\cdot (1-p)=p^2\cdot (1-p{)}^2$。注意在这四次实验中，四次都成功的方法只有1种，三次成功一次失败的方式有四种，两次成功两次失败的方式有6种，一次成功三次失败的方式有四种，全部失败的方式有一种。总的来说，对于n次实验，其中成功x次的方式为
$$C_x^n=\frac{n!}{x!(n-x)!}$$
它其实就是n个物体一次拿出x个的组合的数量。注意一共有$2^4=16$个不同的结果。如果实验n次，每次结果要么是“成功”要么是“失败”，那么就应该会有$2^n$个结果。

让我们按照如下的方式进行分类：
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6VWT3guE-1586708457762)(asserts/figureX-t2.png)]

考虑最后一列的各项。$4p^3(1-p)$表示四次实验中有3次成功的概率。四次实验中成功三次可以有四种方式，如果有3次成功，那么我们一定有一次失败。三次成功一次失败的概率是$p^3(1-p)$，因为有四种结果方式，因此最终的概率是$4p^3(1-p)$。最后一列的表达式表示二项分布的单独项，它的标准形式如下所示：

如果任意实验的成功概率是p，那么
$$P[n实验成功x次]=C_n^x{p}^x(1-p{)}^{n-x}=b(x;n,p)\text{\hspace{1em}(X-1)}$$

$b(x;n,p)$表示概率密度形式的二项分布。概率密度形式会在后边的章节进行讨论。如果读者让n=4，且x的取值范围是0到4，将能看到从公式X-1中得到的前一个例子的概率列中的单独项。

在n次实验中最多获得X成功的概率，以及最少获得X项成功的概率，可以通过将对应的单独项相加来获得。

$$P[n次实验最多成功x次]=\sum _{s=0}^x{C}_n^s{P}^s(1-p{)}^{n-s}\equiv B(x;n,p)\text{\hspace{1em}(X-2)}$$

$$P[n次实验最少成功x次]=\sum _{s=x}^n{C}_n^s{p}^s(1-p{)}^{n-s}=1-\sum _{s=0}^{x-1}{C}_n^s{P}^s(1-p{)}^{n-s}\text{\hspace{1em}(X-3)}$$

其中，B(n;n,p)是累积分布形式里的二项分布（累积分布将会在后一个章节讨论）。在这个阶段，我们可以简单的解释二项式是成功次数小于等于某个值的概率。因此，回到我们的例子，四次实验中成功两次的概率是：

$$6p^2(1-p{)}^{+}4p^3(1-p)+p^4=1-[(1-p{)}^4+4p(1-p{)}^3]$$

二项分布是一个非常大的表格，经常是公式X-2的形式但有时候会是公式X-3的形式，有时候是X-1的形式。可以查看参考资料【1】，【33】，【41】中的例子。

二项分布的统计平均值是np，方差是$np(1-p)$。平均值是分布位置的度量，而方差是分散程度的度量。这些知识会在随后的章节中讨论。

在使用二项式的过程中，我们已经做出了很多的假设。明确的列出这些假设非常重要。

1. 每一次实验都有且只有两个实验结果。我们可以用“正常”“故障”来表示结果，也可以用其他的方式准确表示。
2. 一共有n次随机试验，n是已经确定的数字。
3. 所有n次实验完全独立。
4. 成功的概率可以用p或者其他字母表示，p在实验的过程中是一个不变的常数。

非常重要的一点是，如果问题出现，并违反了上边一条或多条的假设，那么使用二项分布就是有疑问的，除非对违反的效果进行调查。事实上，所有的分布和所有的数学方程的特征都是基于一些假设和限制的，使用这些分布或方程涉及到这些假设和限制的相关方面。

现在让我们重新审视这些假设，假如说其中某一条假设并不成立，那么我们能做什么？我们来看几个违反这些假设的例子。

1. 如果实验的结果不止一个会怎样？在某些测试方法中，会有三个可能的决策：接受批次，拒绝批次，继续实验。如果我们从装有白色、绿色、红色、黄色、蓝色芯片的容器内抽取一个芯片，每一次的实验结果会有5种可能性。这种案例不会构成严重问题，我们简单的用二项分布的扩展方法来取代二项分布，这个方法就是多项分布，该方法在很多统计著作中都有讲到（例如参考资料52）。如果适用，我们也可以将结果分类为“成功”与“失败”，并在更粗略的分类上使用二项式。（在这里“成功”的概率是所有归类为成功的事件的概率的和）

2. 现在我们假设实验的次数n是未知的，但是知道成功的次数。例如，我们扔一个骰子直到扔出一个5.我们并不能事先知道我们要抛多少次。或者，我们可以去测试相似的继电器直到发现一个坏的，同样的，我们不知道需要测试多少次。在这种情况下，我们不能使用二项式，但是另一个和二项分布相关的分布是可以用的，它叫做“负二项分布”（参考资料13）。负二项分布$\hat{b}(x;k,p)$给出了进行到x个实验时第k次成功的概率。
   $$\hat{b}(x;b,p)=C_{x-1}^{k-1}{p}^k(1-p{)}^{x-k}\text{\hspace{1em}(X-4)}$$

3. 如果n次实验的结果是互相依存的（例如第x+1次的结果依赖于前x次的结果或可能与前面的结果有关），困难就会增加好多。需要各种条件概率表示。特定结果顺序概率依赖于发生的次序,每个不同的次序有不同的概率。举个例子，用二项分布来估计是否会下雨就是不可行的事情，因为天气模式一般会持续几天或几周，星期三是什么天气与星期二是什么天气有关。如果独立性存疑，则应该先进行独立性检查在应用二项分布解决问题（参考资料11）。

4. 如果成功的概率在实验的进行过程中发生了变化，当实验的样本选自一个固定的范围且不拿出替换，这时我们能用超几何分布（hypergeometric distribution)解决该问题。这个分布的形式如下：
   $$h(x;n,a,b)=\frac{C_a^x{C}_b^{n-x}}{C_{a+b}^n}\text{\hspace{1em}(X-5)}$$

其中，a是总体中具有特征A的项目数量，b是总体中具有特征B的项目数量，N=（a+b)是总体或批次的大小，n是从总体中抽取样本的大小，x是样本中具有特征A的数量。

举个例子，特征A是有缺陷的，特征B是没有缺陷的。$h(x;n,a,b)$得出恰好n样本中有x个具备特征A的概率。

当从一个小数量总体中进行抽样且不替换时，必须应用超几何分布。（”小“表示N和n在数量上是同一级别的）。举个例子，如果我们接受了50个电感，其中10个有缺陷，那么有问题的部分就有五分之一，但是当我们抽取20个样本而不替换时，该比例会发生变化。

从公式X-5我们可以看出，使用超几何分布涉及到包含阶乘在内的复杂的计算，因为这个原因，二项式经常在此类问题中使用以获得近似的结果。二项分布能在$N\ge 10n$（其中N是总体数量,n是抽样数量，一些作者认为这里应该是$N\ge 8n$）时获得近似结果。在此类问题中，$a/n$近似等于$p$。

一个应用二项分布的特殊例子，考虑如下的问题，ABC公司大量生产一个型号的电阻。以前的经验表明电阻的缺陷率是百分之一。因此，一个采样的缺陷概率$p=0.01$。如果从生产线上一次采样10个电阻，那么其中只有一个缺陷电阻的概率是多少？我们可以得出

$$\begin{gathered} x=1,n=10,p=0.01 \\ b(x=1;n=10,p=0.01)=C_{10}^1\times 0.01\times 0.99^9 \end{gathered}$$

如果二项式分布表可用，我们就可以简单的通过寻找B(1)-B(0)来评估，因为

$$\begin{array}{rl}& B(1)=P[0或1个缺陷电阻]\\ & B(0)=P[只有0个缺陷电阻]\\ & B(1)-B(0)=0.9957-0.9044=0.0913\end{array}$$

为了日后相似的计算，我们可以画一张10个抽样中含有$x=0,1,2,3..10$个故障电阻的概率的分布函数。该分布如图X-1所示，图X-1的曲线并不是十分合理，因为二项分布是离散的，但是这样连续插值可以更好的显示出分布的总体形状。

在可靠性和安全性评估中，如果每一个每一个冗余部件工作独立，且每个冗余部件都有（近似）同样的失效概率，那么二项分布是适用于该冗余系统的。举个例子，假设我们有一个n冗余部件，假设其中多于x个发生故障，则系统就会故障。该系统不发生故障的概率就是小于等于x个部件故障的概率，这正是二项累积概率$B(x;n,p)$。

或者，假设有一种情况中有n个可能发生的事件，倘若多于x件事情发生，则出现灾难。如果n件事情互相独立且发生概率相同。那么二项分布就是适用的。总的来说，当某事件重复n次，我们想直到其中某个结果出现x次，小于x次或者大于x次的概率时，二项分布就是适用的。这里的“n次实验“可以是n个部件，n年，n个系统或者其他适用的数量单位。

我们将短暂的返回二项分布，因为它的两个限制形式对我们很重要。我们将对其分布和分布参数进行讨论研究。

3. 累积分布函数（Cumulative Distribution Function)

让我们用X代表随机实验的可能结果。X经常用来表示随机变量，这个值可能会是离散（比如一个批次里边的数量）的或者连续的（比如重量，高度）。事实上，即使表面上是连续的变量，由于存在测量的分辨率，看起来连续的值也是一个离散变量。将这些量看成是连续的会让数学层面方便一些。用对应的小写字母x来表示一个随机量会更方便一些。

在这里我们需要展现的基本公式将以连续值的形式给出，在需要给出连续值与离散值的不同的地方，我们会加以说明。总的来说，在操作上是用求和富豪来代替整数符号的问题。在累积分布方程中用于表示概率形式的$F(x)$里，我们一般表示X的值要小于等于x的值。

$$F(x)=P[X\le x]\text{\hspace{1em}(X-6)}$$

根据公式X-6，因为F(x)是个概率，因此

$$0\le F(x)\le 1$$

如果X的取值范围是负无穷到正无穷，那么

$$\begin{gathered} F(-\infty )=0 \\ F(+\infty )=1 \end{gathered}$$

如果X有更小的限定$x_1<X<x_u$，那么

$$\begin{gathered} F(x_1)=0 \\ F(x_u)=1 \end{gathered}$$

F(x)有个很重要的性质是随着x的增加，它的值是不会减小的。在严格的数学含义上，它是一个非减函数，但是不一定单调。它可以更简洁的表示如下：

If$x_2>x_1$, then$F(x_2)\ge F(x_1)$

一个更重要的性质如公式X-7所示：
$$P[x_1\le X\le x_2]=F(x_2)-F(x_1)\text{\hspace{1em}(X-7)}$$

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oqkWE3Xc-1586708457765)(asserts/figureX-2.png)]

我们在第二节遇到的二项累积分布B(x;n,p)是F(x)一种特殊形式。F(x)连续和离散变量的标准形式如图X-2所示。

我们展现在上边方程中的累积分布函数的性质对离散和连续随机变量是有效的。

举一个随机变量和对应的累积分布的例子，在一个随机试验中，我们观察一个单独的器件的故障次数。每当该部件故障，我们就修好它，将时间t归0，并记录下次故障的时间。

我们假设维修并不会改变部件故有性质，也就是说每次维修都会让部件回到初始状态。随机变量T是初始化或维修后到发生故障的时间。我们用$t_i$来表示T的特定值。累积分布$F(t)$用来表示任意给定故障时间少于或等于t的概率。

另一个例子，我们针对某样物体进行反复的测量。随机变量X表示测量结果，$x_i$表示某次测量结果。累积分布F(x)表示测量值小于或者等于x的概率。我们能从$F_{est}(x_i)$来估计$F(x)$，其中
$$F_{est}(x_i)=\frac{n_i}{n}$$

n是测量的总次数，$n_i$是测量的X小于等于$x_i$的测量次数，随着n不断的变大，$F_{est}(x_i)$也在不断的接近$F(x_i)$。在应用中，累积分布函数必须根据理论思考来确定，或者通过统计方法估算。

4. 概率密度函数(probability Density Function)

对于连续随机变量，概率密度函数(probablity desity function,简称pdf),f(x)，可以通过F(x)微分的方式获取。

$$f(x)=\frac{d}{dx}F(x)\text{\hspace{1em}(X-8)}$$

它的等效形式是

$$F(x)={\int }_{-\infty }^{x}f(y)dy\text{\hspace{1em}(X-9)}$$

因为f(x)是非递减函数的斜率，我们有

$$f(x)\ge 0\text{\hspace{1em}(X-10)}$$

若概率函数在整个范围内进行积分，那么结果是统一的。

$${\int }_{-\infty }^{\infty }f(x)d(x)=1\text{\hspace{1em}(X-11)}$$

$f(x)$的性质使得我们可以把其下的区域看成概率。

概率密度的基本含义可以用公式X-12表示：

$$f(x)dx=P[x<X<x+dx]\text{\hspace{1em}(X-12)}$$

我们前边的公式X-7可以用另外一种特别有用的形式表示：

$$P[x_1\le X\le x_2]={\int }_{x_1}{x}_{2}f(x)dx\text{\hspace{1em}(X-13)}$$

f(x)的标准形状阐述于图X-3，其中a是一个对称分布，b是一个向右倾斜的分布，c是向左倾斜的分布。（在图中，x增加相当于图形右移）。

在持续变量的情况下，概率必须用区间表示。这是因为对于指定的x值的概率一直等于0，因为在任意区间中有无数个X的值。因此$f(x)dx$是目标落在x和x+dx区间的数量的概率。当然，dx的区间长度应该尽可能的小。f(x)本身也就是单位区间的概率。在这个例子中，我们用加法符号来替代积分符号，将所有目标区间的x的概率加起来。公式X-13将适用于所有离散的X。

在先前故障案例中，$f(t)dt$给出了部件在t和t+dt之间发生故障的概率。在测量的例子中，f(x)dx给出了测量结果位于x和x+dx之间的概率。从经验角度出发，如果我们考虑大量的测量，f(x)dx可以用以下公式进行估计
$$f(x)\delta x=\frac{\delta n_i}{n}$$
这里n是测量的总次数,$\delta n_i$是X位于x和$x+\delta x$之间的数量。

5。 分布参数和矩

特定概率密度函数的特征是通过分布参数描述的。一类参数用于沿着横坐标定位分布。因此，像这类的参数被称作位置参数（location parameter)。

最常见的位置参数是统计平均数。其他常用到的位置参数有：中值（median)（50%在概率密度曲线下方的区域在中值的左边；另50%在右边）；模（mode)，位于概率曲线的最大值或“峰值”上（在二项分布或三项分布中，可能会没有最大值或有多个最大值的情况）；中列数（mid-range）,当变量在有限的区间内，它是最大值和最小值的平均值，除此之外，其他的都不很重要。图X-4展示这些概念。

在（a)中，中值用$x_{.50}$表示。从中值的定义中可以看出，50%的次数结果将会小于等于$x_{.50}$，而50%的次数，将会大于。因此$P(x\le x_{.50})=.50$，根据累积分布，$F(x_{.50})=.50。中值是$\alpha$百分数的特殊例子，$x_\alpha$定义为F(x_{\alpha })=\alpha$，例如，90%百分数是$F(x_{.90})=.90$，90%的次数中结果中的x数值将会小于等于$x_{.90}$。

在（b）中，模是用$x_m$表示，给出了最大概率的结果的值。在©中，我们看到如何从两个极值中得出中列数。

均值（average）也被成为平均值（mean）或期望值（expected value）。如果我们重复做相同的随机实验，对结果取平均值。那么这个实际平均值会随着实验次数的增加越来越接近理论平均值。（我们假设分布存在平均值，这样实验平均值会越来越趋向于总体平均值）

在图X-3（a)中那样的对称分布的情况下，均值，中值和模是统一的。对于倾斜的分布，如图X-3（c)，中值将落于模和均值之间。在图X-5中，这两个对称分布图形有着相同的均值，中值和模。但是对于中心聚集程度的角度来看，它们却是不一样的。用来描述这分布这方面的参数叫分散参数（dispersion parameters）。其他和这个类似的参数还有方差（variance）、方差的开方和标准差（standard deviation）。其他分散参数比较少用到，是种植绝对偏差（median absolute deviation),范围在上限值和下限值之间。我们将会在后一章里边计算方差。

事实上，还有很多其他的分布参数，我们这里涉及到的都是一些基本的参数。当累积概率分布的形式确定后，我们必须掌握计算分布参数的具体方法。这些通用方法中的一些方法需要计算分布中的矩，并且在理论统计中十分重要。分布的矩可以在任意指定点上计算，但是我们限制只在（a)中计算原点的矩，(b)中计算均值的矩。

(a) 原点的矩

第一个关于原点的矩被定义如下：

$${\mu }_1^{\prime }={\int }_{-\infty }^{+\infty }xf(x)dx\text{\hspace{1em}(X-14)}$$

它表示X的平均或期望值，用$E[X]$表示。我们使用$\mu$来简单的表示均值，因为$E[X]=\mu$。

第二个关于原点的矩被定义如下：

$${\mu }_2^{\prime }={\int }_{-\infty }^{+\infty }{x}^{2}f(x)dx\text{\hspace{1em}(X-15)}$$

他表示$X^2$的期望值，$E[X^2]$。

总而言之，第n个关于原点的矩是

$${\mu }_n^{\prime }={\int }_{-\infty }^{+\infty }{x}^{n}f(x)dx\text{\hspace{1em}(X-16)}$$

表示$X^n$的期望，$E[X^n]$

如果$Y=g(X)$是任意关于X的函数，X是根据概率密度函数f(x)的分布，$g(X)$的期望可以通过如下方式获得：
$$E[Y]=E[g(X)]={\int }_{-\infty }^{+\infty }g(x)f(x)dx\text{\hspace{1em}(X-17)}$$

(b)均值的矩

第一个关于均值的矩定义如下：

$${\mu }_1={\int }_{-\infty }^{+\infty }(x-\mu )f(x)dx\text{\hspace{1em}(X-18)}$$

因为它总是等于0，所以并没有什么用处。

第二个关于均值的矩的定义如下：
$${\mu }_2={\int }_{-\infty }^{+\infty }(x-\mu {)}^{2}f(x)dx\text{\hspace{1em}(X-19)}$$

它表示了方差${\sigma }^2$或者$E[(X-\mu)^2f(x)dx]。总的来说，均值的第n个矩定义如下：

$${\mu }_n={\int }_{-\infty }^{+\infty }(x-\mu {)}^{n}f(x)dx\text{\hspace{1em}(X-20)}$$

表示$E[(X-\mu {)}^n]$。

有一个非常有用的关系：

$${\mu }_2={\mu }_2^{\prime }-({\mu }_1^{\prime }{)}^2\text{\hspace{1em}(X-21)}$$

公式21允许我们通过评估X-15中的积分，而不是X-19中更复杂的积分来计算方差。公式21可以通过如下方式得到轻易的证明：

在离散随机变量的情况下，原点的第一个矩表示为：

$$\mu ={\mu }_1^{\prime }=\sum _{i=1}^n{X}_{i}p(x_i)\text{\hspace{1em}(X-22)}$$

这里$p(x_i)$是$x_i$的概率，最常用的寻找n个值的平均值的方程如下：

$$\hat{x}=\frac{1}{n}\sum _{i=1}^n{x}_i$$

这是公式22应用的特殊情况，每个值都被认为拥有同样的出现的概率$\frac{1}{n}$。

例如，对于单一的骰子，我们有

$$\mu ={\mu }^{\prime }=\frac{1+2+3+4+5+6}{6}=3.5$$

尽管实际上不会出现这样的结果，但是期望值是3.5.

同样的，如果随机变量是离散的，那么第二个均值的矩的形式如下：

$${\mu }_2=\sum _{i=1}n(x_i-\mu {)}^{2}p(x_i)\text{\hspace{1em}(X-23)}$$

在所有$x_i$都有同样的“权重”1/n的情况下，公式X-23可以简化成计算n个读书采样的方差的采样等式：

$$s^2=\frac{1}{n}\sum _{i=1}n(x_i-\hat{x}{)}^2\text{\hspace{1em}(X-24)}$$

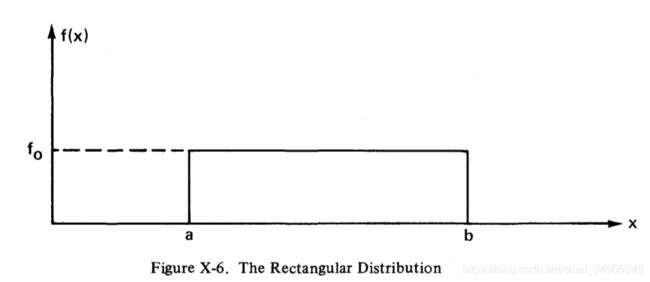
我们用一个应用分布矩的简单例子来总结这一节的内容。参考如图X-6那样的矩形概率密度函数，它在a和b中的任何值基本都是相等的，因为都相等，所以$f(x)=f_0$。因此，这个概率密度函数的积分应该是1，我们有：
$Area=f_0(b-a)=1$，于是$f_0=\frac{1}{b-a}$。

分布的均值（期望）计算如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-cVvsse9F-1586708457771)(asserts/equationX-2.png)]

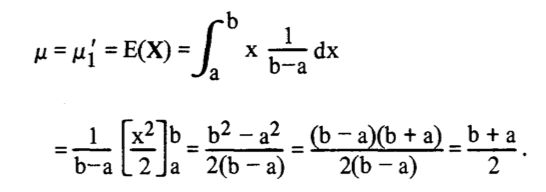
分布的方差计算如下：

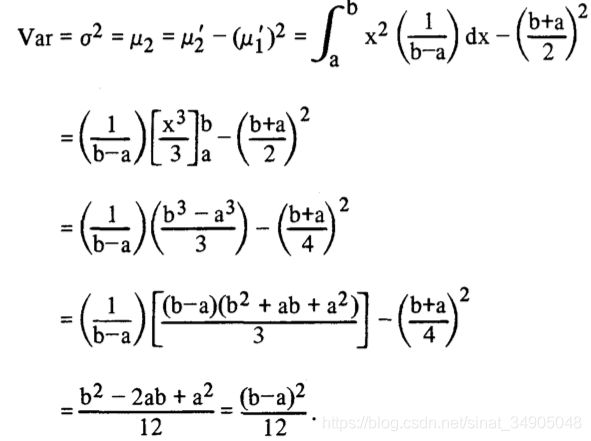
10.6 二项式的极限形式：正态分布和泊松分布

有一些很重要的分布是二项分布的极限形式。例如：
$$\underset{n\to \infty }{\lim }[C_n^x{p}^x(1-p{)}^{n-x}]$$

上面的式子是p是固定的，n趋近于无穷的一种极限形式。省略数学细节，该过程会转换成著名的正态分布形式：高斯分布。

$$f(x;\mu ,\sigma )=\frac{1}{\sqrt{2\pi }\sigma }exp[-\frac{1}{2}(\frac{x-\mu }{\sigma }{)}^2]\text{\hspace{1em}(X-25)}$$

这里$\mu$和$\sigma$是平均值和标准差。正态分布已经广泛的应用表格进行处理，但不是X-25那样的形式。X-25那样的表格需要对$\mu$和$\sigma$进行广泛的覆盖，这将使得表格过于臃肿而降低可用性。找到一种转换形式，将$\mu$和$\sigma$标准化，变成0和1，这是有可能的。这种转换是：

$$z=\frac{x-\mu }{\sigma }\text{\hspace{1em}(X-26)}$$

对应的基于z的表现形式为

$$f(z)=\frac{1}{\sqrt{2\pi }}{e}^{-z^2/2}\text{\hspace{1em}(X-27)}$$

这个式子被叫做标准正态分布，它是所有正态分布表格的基本形式。

读者注意到，从公式X-25经由公式X-26到公式X-27，并不是一个简单的替换的过程。这个变换用到了转换的雅克比式（参考【25】）。在这个例子中，雅克比式是$\sigma$，这里抵消了$1/(\sqrt{2\pi }\sigma )$中的$\sigma$。$f(z)$的图形如图X-7所示：

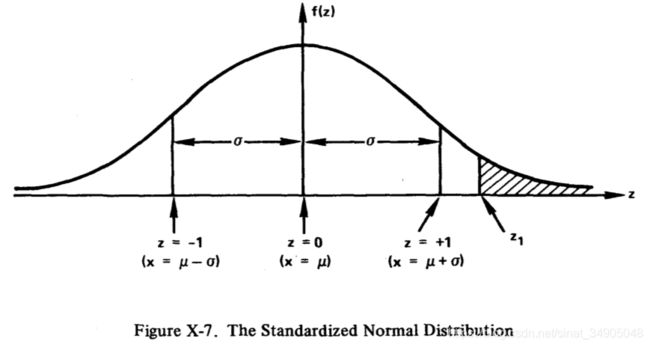
这里列举了一些标准正态分布的几个特征。其中我们最感兴趣的是曲线之下横轴上的两个点之间的部分。读者应该还记得这样的区域可以当成一个概率，因为曲线下的所有区域之和是一致的。假设存在一个点$z_1$，一些表格记录了从$z_1$到$+\infty$的曲线下的区域（图中的阴影部分）；一些表格记录了从$z_1$到$-\infty$的曲线下的区域，还有一些表格记录了从$z_1$到原点的曲线下的区域。当然，在智能的使用表格之前，必须确认要制表的区域。

对于正态分布，对于原始的变量X，$\sigma$衡量了平均值$\mu$到曲线拐点的距离，概率密度曲线从$\mu -\sigma$到$\mu +\sigma$的区域约等于0.68，从$\mu -2\sigma$到$\mu +2\sigma$约等于是0.95.

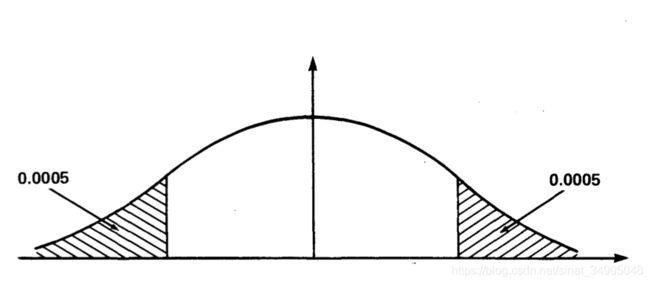
这里假设读者已经熟悉正态分布和它的表格。尽管如此，我们还是给出一个简答的数学实例，有经验的可以略过。锻件中的槽的宽度符合正态分布，它的均值$\mu$等于0.900英寸，标准差$\sigma$等于0.0030英寸。如果说明书中的限制（允许误差）为$0.9000\pm 0.0050$,占有总产出多少百分比的数将被拒绝？拒绝的锻件是其宽度数值是在图中阴影部分的那些。

对于x=0.9050的z值为
$$z=\frac{0.9050-0.9000}{0.0030}=1.67$$

从标准正态表格可以得出，右边的尾巴区域在$P[Z\ge 1.67]$等于0.0475。这是$X\ge 0.9050$的概率。由于图形是对称的，所以左边的尾巴区域也是0.0475.所以两边尾巴加在一起的就是0.0950.这就是一个零件宽度在说明书外的概率。因此，9.5%就是零件被退回的概率。

这个退回率相当高。如果说明书不做更改，我们可以通过认真工作，降低$\sigma$来降低退回率。假设我们的目标退回率是1/1000=0.001,那么最大允许的退回率$\sigma$,这里记为${\sigma }^{\prime }$，应该是多少？

如果退回率是0.001，则每个尾巴上的区域必须是0.001/2=0.0005。从表格中得出，截去0.0005区域尾巴的z的值是3.3。从$z=(x-\mu )/\sigma$我们可以得出${\sigma }^{\prime }=(x-\mu )/z$，

因此 ${\sigma }^{\prime }=\frac{0.9050-0.9000}{3.3}=0.00152英寸$。

因此，对于0.001的退回率，最大允许$\sigma$的值是0.00152英寸。

我们研究正态分布有很多种理由。其中之一就是根据中心极限定理，不管每个测量的分布如何，大量的测量的均值就趋近于正态分布。另一个理由是正态分布为许多消耗模型提供了相当好的统计模型。

从系统和可靠性分析的角度出发，另一种重要的形式是以下二项分布的极限形式：
$$\begin{gathered} \underset{n\to \infty \\ p\to 0}{\lim }\{C_n^x{p}^x(1-p{)}^{n-x}\}\text{\hspace{1em}(X-28)} \end{gathered}$$

在公式X-28中，这个极限采用了这样一种形式来使得np保持有限。这个极限过程的结果为

$$\frac{(np{)}^x}{x!}{e}^{-np}=\frac{m^x}{m!}{e}^{-m}\text{\hspace{1em}(X-29)}$$

这里m=np。（这个数学过程可以在很多参考资料中找到，例如参考【32】，45-46页）

公式29给出了稀有事件（$p\to 0$）在大量试验下（$n\to \infty$），精确的x的发生概率。事件预期的发生次数是$np=m$。公式X-29的分布就是泊松分布。如同矩的方法展示（虽然有更简单的方法），泊松分布的均值和方差在数值上都等于m。

即使p不是特别小，n也不是特别大，泊松分布还是能很好的近似二项分布。举个例子，假设在批量生产过程中遇到不合格产品的概率是0.1（即p=0.1），那么在一批次10个零件中（n=10）发现不合格产品正好是1个的概率是多少？准确的数值可以通过二项分布得到
$$b(1;10,0.1)=0.3874$$
泊松分布可以得到近似结果为0.3679，于实际值相差不大。如果我们提高批次的数量到20（n=20），则结果更加接近:二项分布为0.2702，泊松分布为0.2707.

泊松分布非常重要，不仅因为它能近似计算二项分布，而且它能描述很多稀有事件的性质，而不论其潜在的物理过程如何。泊松分布在描述稳态系统组件或系统的故障发生方面还有很多应用。我们将在后边的章节描述这些系统应用方式。

10.7 针对系统故障的泊松分布应用——指数分布

假设我们有一个稳态系统，它不在燃烧或损耗状态。我们进一步假设，当它失效时，它会恢复到初始状态，维修的时间可以忽略。我们的关注点是系统故障。我们着重关注系统出现故障的次数为0次的概率。因此，在泊松分布中，我们在公式X-29中令x=0。其结果是：
$$P[系统故障次数为0]=e^{-m}$$
其中，m为大量的实验中系统预期的故障数。

现在，就系统失效而言，我们关注的参数是时间。因此我们要寻找如何用时间来表达m。这件事很简单。

假设我们有系统的数据，平均每50小时系统就会故障。我们说故障的平均时间（$\theta$）就是50小时。如果我们让系统工作100小时，我们预计会遇到两次失败，因为100/50=2。采用符号t表示工作时间，我们有

$$时间t内我们预计的故障次数=t/\theta =\lambda t$$，这里$\lambda =1/\theta$。

但是m为预计的故障次数。因此
$$P[系统故障0次]=e^{-m}=e^{t/\theta }=e^{\lambda t}$$。

现在，系统的可靠性，R(t)通过时间t内持续正常工作的概率来定义。因此我们有：
$$R(t)=e^{-t/\theta }=e^{-\lambda t}\text{\hspace{1em}(X-30)}$$

时间t之前系统出现故障的概率由累计分布函数F(t)给出。系统可能在时间t前失效或者不失效，因此我们有
$$R(t)=e^{-\lambda t}=1-F(t)$$
以及
$$F(t)=1-e^{-\lambda t}\text{\hspace{1em}(X-31)}$$
有关公式X-31的概率密度函数现在可以轻易的得出
$$\begin{gathered} f(t)=\frac{d}{dt}F(t)=\frac{d}{dt}(1-e^{-\lambda t}) \\ f(t)=\lambda e^{-\lambda t}\text{\hspace{1em}(X-32)} \end{gathered}$$
公式X-32中的概率密度函数通常指的是“失效时间的指数分布”。公式X-30在某些时候简称是实数分布。

公式X-30，X-31，X-32给出的可靠性、累计分布、概率密度函数，在系统分析和可靠性方面用处非常广泛。原因很简单，指数分布是个非常简单的分布。只有一个参数（故障率或故障平均时间）必须通过经验确定。但是我们必须十分小心的应用公式X-30来计算系统可靠性。因为公式X-30来自于泊松分布。而后者是二项分布的极限形式。二项分布被我们在前一章所列举的很多假设所限制。在极限过程中一些假设被修改。但其中之一并没有涉及。这个假设就是所有的实验都是互相独立的。换句话说，一个实验就是在某个时间段有机会发生故障。

当系统故障是可修复的，我们关于独立实验的假设。解释如下。在未来某时段故障的概率是一个只和时间段长度有关的函数，和过去的故障次数无关。如果系统是不可修复的。则我们的假设需要更改成如下的形式：没有先前的故障，对于不可修复的部件，如果我们在一个靠前的时间出现了一次故障，那么在某一个后边时刻，它的已发生故障的概率是1，后续发生故障的概率是0，以为事件已经发生了。

表征故障过程的另一种方法如下。对于指数分布，到时间t还没有出现故障，那么在(t,t+$\delta t$)时段中发生故障的概率和同样时间长度的其他时段概率是相等的（到该时段还未发生故障）。它和(0,$\delta t$)时间段的故障概率是相同的。因此，因为我们从t=0开始运行系统，在时间t上我们的系统“和新的一样”，这是指数分布的另外一种描述。

如果我们从假设出发——在特定时间段里故障的概率是一个只和时间段的长度有关的函数，我们能单独从这个假设中得到指数分布。假设一个不可修复的系统，他能存在于两种状态之一：$E_1$为系统工作,$E_0$为系统故障。我们定义

$$\begin{gathered} P_1(t)=在时间t系统在E_1状态的概率 \\ {P}_0(t)=在时间t系统在E_0状态的概率 \end{gathered}$$

假设开始时系统处于$E_1$状态.

现在$P_1(t+\delta t)$表示系统在$t+\delta t$时系统处于状态E1的概率。我们有
$$P_1(t+\delta t)=P_1(t)[1-\lambda \delta t]=P_1(t)-P_1(t)\lambda \delta t$$

这里，根据我们开始的假设（系统故障概率只和时间段的长度有关），$\lambda \delta t$给出的系统在时间段$\delta t$中从状态E1到E0的转换概率，$\lambda$是一个常数（失效率）。因此$(1-\lambda \delta t)$表示系统在$\delta t$时刻没有从E1到E0的概率。代数重排产生了如下的差分方程。
$$\frac{P_1(t+\delta t)-P_1(t)}{\delta t}=-\lambda P_1(t)$$
如果我们让时间段的长度接近0，根据定义，方程左边的极限形式就是$P_1(t)$关于t的导数。
$$\underset{\delta t\to 0}{\lim }[\frac{P_1(t+\delta t)-P_1(t)}{\delta t}]=\frac{d}{dt}{P}_1(t)=P_1^{\prime }(t)=-\lambda P_1(t)$$
这是关于时间微分的主要观点，是由牛顿提出。我们现在有了微分方程：
$$P_1^{\prime }(t)=-\lambda P_1(t)$$
如果我们记得限制条件$P_1(t=0)=1$，则这很容易整合。
$$\begin{array}{rlr}& \frac{d[P_1(t)]}{P_1(t)}=-\lambda dt& \\ & [ln{P}_1(t){]}_0^t=[-\lambda t{]}_0^t& \\ & ln{P}_1(t)-ln1=-\lambda t& P_1(t)=e^{-lambdat}\end{array}$$
这正是系统的可靠性，因为$P_0(t)+P_1(t)=1$，我们有
$$P_0(t)=1-e^{-\lambda t}=1-R(t)=F(t)$$

对应的概率密度函数是
$$f(t)=\lambda e^{-\lambda t}$$
我们认识到这是指数分布。

10.8 失效率函数

上一章中
$$F(t)=P[t之前发生故障的]$$
$$f(t)dt=P[t和t+dt之间发生故障]$$
我们现在定义一个条件概率，$\lambda (t)$，叫做失效率函数（failure rate function）
$$\lambda (t)dt=P[故障在t和t+dt间发生|先前没有发生故障]\text{\hspace{1em}(X-33)}$$

对于任意常规分布，有一个重要的性质：
$$\lambda (t)=\frac{f(t)}{1-F(t)}\text{\hspace{1em}(X-34)}$$
该式证明如下.
我们用T来表示失效发生的时间。T是一个随机变量，定义如下：
$$\lambda (t)dt=P[t<T<t+dt|t<T]$$
让我们用(t $$P(A|B)=\frac{P(A\bigcap B)}{P(B)}$$
因此
$$\lambda (t)dt=\frac{P[(t<T<t+dt)\bigcap (t<T)]}{P(t<T)}$$
现在事件A是事件B的一个特例。当A发生，则B自动发生，在集合理论中，A是B的一个子集，在这些条件下，$A\bigcap B=A$。于是
$$\lambda (t)dt=\frac{P[t<T<t+dt]}{P(t<T)}=\frac{P[A]}{P[B]}=\frac{f(t)dt}{1-F(t)}$$
最终
$$\lambda (t)=\frac{f(t)}{1-F(t)}$$
这也就是公式X-34.
如果我们为一个系统画出关于时间的$\lambda (t)$，则曲线如图X-8所示。这个曲线呈现浴缸的样子。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-txmufdU3-1586708457778)(asserts/figureX-8.png)]

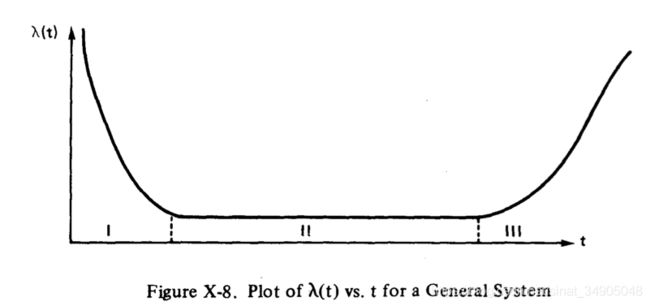
图8的曲线可以分成I，II，III的三部分。I区被称为“婴儿死亡率区域”，这个区域很难确定分布。适合这部分曲线的分布可能取决于系统本身的特性。制造商经常要对产品进行老化测试，以降低批量产品运送给顾客前的早期故障。II区对应“一个常数故障率”，是指数分布适用的机会失败区域。区域III对应磨损过程，正态分布经常为此提供一个适当的模型。对于一个真实的系统，$\lambda (t)-t$曲线经常与图X-8的描述差异较大。例如，区域II的指数分布经常整个消失，或者老化区域是可以忽略的。

返回故障率方程，可以很方便的对X-34的F（t）和f(t)求解。通过以下形式改写X-34来完成。
$$\lambda (t)dt=\frac{[-F^{\prime }(t)dt]}{1-F(t)}\text{\hspace{1em}(X-35)}$$
其中$F^{\prime }(t)=\frac{dF(t)}{dt}$.
对X-35两边取积分，得到
$$-{\int }_0^t\lambda (x)dx=ln[1-F(t)]$$
它等效于
$$1-F(t)=exp[-{\int }_0^t\lambda (x)dx]$$
因此$$F(t)=1-exp[-{\int }_0^t\lambda (x)dx]\text{\hspace{1em}(X-36)}$$
如果我们对X-36取微分，我们有
$$f(t)=\lambda (t)exp[-{\int }_0^t\lambda (x)dx]\text{\hspace{1em}(X-37)}$$
假如我们令$\lambda (t)=\lambda =常数$，那么对于X-36和X-37，我们有
$$\begin{gathered} F(t)=1-e^{-\lambda t} \\ f(t)=\lambda e^{-lambdat} \end{gathered}$$
这是一个指数分布。对于该指数分布，然后，故障率是一个常数（仅依赖于时间t），
$\lambda (t)dt=P[故障发生在t和t+dt之间|以前没有发生故障]=\lambda dt$
如果我们选择采用指数分布来描述部件的故障分布。我们假设我们处于“浴缸曲线”中恒定的，稳态的部分，没有老化和磨损的发生。因为故障率是一个常数，指数分布通常指作为“随机故障率分布”，如以后的故障概率依赖于以前时序正常工作时间。

如果我们采用$e^{=t/\theta }$来表示可靠性也是十分有价值的，即使是磨损发生（但不是老化），我们这里依旧是保守的。例如$R(t)\ge e^{-t/\theta }$，这里R(t)是实际上的可靠性，$\theta$是实际的故障平均时间。对于$t\le \theta$这个关系是真实的（参考[15]）。

公式X-36，X-37可以用来评估多种不同类型的故障率模型。例如，如果$\lambda (t)=kt$（线性增加的故障率）我们可以得出
$$R(t)=1-F(t)=exp(-k{t}^2/2)$$
这被叫做瑞利分布。一个时间故障率相关的重要分布，通过将$\lambda (t)=K{t}^m(m>-1）$代入，可以获得威布尔分布.
$$f(t)=k{t}^{m}exp(-\frac{k{t}^{m+1}}{m+1})$$
和
$$R(t)=1-F(t)=exp(-\frac{k{t}^{m+1}}{m+1})$$
威布尔分布是两参数的分布，k是比例参数(scale parameter)，m是形状参数(shape parameter)。对于m=0，我们得到指数分布，当m增加，一个磨损行为就被建模。当m增长到2，f(t)则变成正态分布。当m小于0但是大于-1，则浴缸曲线的老化区域的模型就被建立起来。因此，改变m的值，我们能使用威布尔分布来包含浴缸曲线的I，II，III区域。读者可以从其他的文献中找到威布尔分布的更多的讲解。（参考【23】p137-138, 附录D，[36] p190）

10.9 一个涉及时间-失效分布的应用

时间-失效分布的概念是十分重要的，为了加深读者的印象，我们设计了如下的例子。

我们从两个供应商那里买了相似的部件A和B。供应商A声称平均寿命是100小时（${\theta }_A=100$小时），并声称其时间-失效分布是指数分布。B的平均寿命也是100小时，但是它的时间-失效分布是正态分布，其均值是100小时，标准差是40小时。

让我们尝试计算这两个部件的10小时工作时间的可靠性。首先，我们考虑部件A。
$$\begin{gathered} R_A(t)=e^{-t/{\theta }_A} \\ {R}_A(10)=e^{-10/100}=e^{-0.1}=0.905 \end{gathered}$$
因此，对于部件A，它的可靠性是90.5%。

现在让我们考虑部件B。它的分布是正态分布。我们需要找到对应t=10小时的变量z的值。
$$z=\frac{t-{\theta }_B}{{\sigma }_B}=\frac{10-100}{40}=-2.25$$
这个值是z去掉尾部区域的0.01222（从标准正态表），表明了10小时之前的失效概率。因此
$$R_B(t=10)=1-0.01222=0.988$$
B的可靠性是98.8%。
根据以上的内容，我们发现尽管${\theta }_A={\theta }_B$，但是$R_A$和$R_B$还是不一样。这个结果不同因为他们的分布是不同的。当t增加，最终指数分布会比正态分布有更高的可靠性。例如，对于t=100小时，$R_A=36.8$，$R_B=50.0$，但是对于t=200小时，这两个分布都会有相同的可靠性。读者可以计算下给定R_A=R_B$下t的值。

10.10 统计估计

假设我们参加洛杉矶地区中20到30岁的男人身高的研究。这是一个很大的总量，尽管我们想要去测量诶一个人的身高，但是实际上是不允许的。
我们采用一个妥协的方式解决该问题，我们从总量里边进行随机采样。随机采样的重要性将在后边叙述。从样本中，我们能估计任意感兴趣的参数，例如样本的均值，样本的中值，样本的方差等。现在的问题是，对于总量的采样统计这个方法到底怎么样？事实上，我们是否能保证样本均值比样本中值或中位数在总体均值中更好？为了回答这个问题，我们需要准确的了解诸如此类语句在统计上的含义。

“$\widehat{{\theta }_a}$”表示总量参数$\theta$的好的估计方法
“$\widehat{{\theta }_b}$”表示总量参数$\theta$的最好的估计方法
“$\widehat{{\theta }_b}$”是比$\widehat{{\theta }_c}$更好的估计方法（//TODO:这里没看懂，是不是应该是a?）

这些问题将在第十三章重新讲解。首先我们必须讨论选择随机样本的重要性，然后我们必须建立抽样分布的概念，特别是均值的抽样分布。

10.11 随机样本

一个随机样本，表示在一个总体中每一个样本都有相同的机会被涵盖（采样）。大多数统计计算是基于随机假设的；如果一个结论是通过看似是随机的，但实际上是反应某些总体特征的样本得出的，那么这个结论一定是大错特错的。

一个经典的随机假设是无效的例子，在1936年的Literary Digest投票上。投票想要做一个抽样调查，目的是看罗斯福和蓝盾谁能当选美国下一任总统。投票显示蓝盾将获胜，然而实际上却是罗斯福通过11069785票的普遍多数和523比8的选举人票数赢得了选举。在这个例子里，投票大部分是通过电话进行。在当时的经济大萧条时期，拥有电话的人大部分是富裕的共和党人，他们都倾向于投票给蓝盾。通过非随机样本做出的结论有明显的错误。在此之后不久Literary Digest就不复存在了。

如果想要在刚获取的一箱样本中进行随机抽样，那么只从箱子上边拿是不对的。如果你这样做了，你可能得到了过于乐观的结论，因为有可能箱子在运输过程中跌落，导致下边的部件都是故障的。不论何时进行抽样，必须小心保证抽样的随机性因为所有的估计技术都是基于随机抽样的。一个简单的方法，就是利用随机数表来保证抽样的随机性。其他随机抽样的方法在资料【10】有详细的描述。

10.12 抽样分布

假设从某总量中抽取样本的数量为n，并计算样本的均值$\overline{x_1},其中$\overline{x_1}=\frac{1}{n}\sum_{i=1}{n}x_i$，我们现在能进行第二次数量为n的抽样，并计算它的均值$\overline{x_2}$。采用类似的方式，我们能生成其他的采样均值，$\overline{x_3},\overline{x_4},\overline{x_5}$等。我们并不期望这些均值都相等。事实上，这些均值都是随机变量。我们将样本均值用$\overline{X}$表示，它代表随机变量。问题来了，$\overline{X}$是如何分布的？所谓的受限中心极限定理(restricted central limit theorem)提供了部分答案，它是这样说的：

如果X（随机变量）是按照均值$\mu$，方差$\sigma$进行正态分布的，那么$\overline{X}$是按照均值${\mu }_{\overline{X}}=\mu$，方差$({\omega }_{\overline{X}}{)}^2={\omega }^2/n$进行正态分布的，n是样本大小。

这个定理只在总体数量是无限大的情况下才是完全正确的。对于有限的总量为N，样本大小为n，则
$$({\omega }_{\overline{X}})=\frac{{\omega }^2}{n}(\frac{N-n}{N-1})$$

更重要的是，一般的中心极限定理，指的是如果X是按照均值$\mu$和方差${\omega }^2$分布的，但是其他的分布是未知的，$\overline{X}$的分布和均值$\mu$和方差${\omega }^2/n$非常接近，最少对于很大的n来说是这样的(n大于等于50)。

因此，不论何时我们处理大样本的均值，我们都会关注正态分布。均值采样分布的方差随着样本大小的增加而减少，这为尽可能多的采集样本数量提供了依据。注意针对$\overline{x}$的z变换为
$$z=\frac{\overline{x}-\mu }{\omega /\sqrt{n}}$$

其他评估的方法（例如中位数，范围，方差等）的特征在于其对应的采样分布，其中的大部分可以在统计学的进一步资料中找到（例如参考【30】）。比如，对于一个正态分布，方差估计值$s^2$是卡方分布得到的${\chi }^2$的函数。

$${\chi }^2=\frac{(n-1)s^2}{{\sigma }^2}$$

卡方分布已经被广泛的制表，并大量应用于决策准则，拟合判断优度分析，以及假设测试。

10.13 点估计——总述(//TODO: Check General meaning )

从样本中计算单一的数值（比如$\overline{x}$），构成了对应参数的点估计。代表值集合的相关随机变量称为样本估计量。为了便于描述，我们定义$\theta$代表要估计的总量参数，$\widehat{{\theta }_a},\widehat{{\theta }_b},\widehat{{\theta }_c}$表示$\theta$中要估计的各类样本。例如，如果$\theta$表示总量的平均值，那么$\widehat{{\theta }_a}$就可以表示样本均值估计量;$\widehat{{\theta }_b}$代表中位数估计；$\widehat{{\theta }_c}$代表中间范围估计，等等。
$\widehat{{\theta }_a},\widehat{{\theta }_b},\widehat{{\theta }_c}$估计量都有采样分布。读者应注意，以下的估计量特征与采样分布有关。

a) 无偏估计量

如果一个估计量的采样分布存在这样一个均值，该均值与被估计的总量参数相等，那么这个估计量叫做无偏估计量。因此，如果$\widehat{{\theta }_a}$是一个总量均值$\mu$的无偏估计量，那么
$$E(\widehat{{\theta }_a})=\mu$$
从期望的属性中，我们知道样本均值$\overline{X}$是一个$\mu$的无偏估计量，因为$E(\overline{X})=\mu$。另一方面
$$S^2=\frac{1}{n}\sum _{i=1}^n(X_i-\overline{X}{)}^2$$
是${\sigma }^2$的偏差估计量。如果我们乘以$n/(n-1)$(贝塞尔修正)我们有
$$S^2=\frac{1}{n-1}\sum _{i=1}n(X_i-\overline{X}{)}^2$$
这是${\sigma }^2$的无偏估计量。

b) 最小均方差估计量和最小方差估计量

一个估计量的均方差定义如下：
$$MSE=E(\hat{\theta }-\theta {)}^2\text{\hspace{1em}(X-38)}$$
MSE是一个衡量估计值$\hat{\theta }$偏离真实值$\theta$的总量的一个方法。通过在公式X-38的圆括号中加上或减去$E(\hat{\theta })$，并利用该结果，我们能重写MSE为如下形式：
$$MSE=E[\hat{\theta }-E(\hat{\theta }){]}^2+[E(\hat{\theta })-\theta {]}^2$$
右手边的第一项是估计值的方差，第二项是估计值偏差的平方。如果估计是是无偏的，那么$E(\hat{\theta })=\theta$，且
$$MSE=E[\hat{\theta }-E(\hat{\theta }){]}^2$$
因此对于无偏估计量的MSE是简单的估计量的方差。

如果针对多个估计量$\widehat{{\theta }_a},\widehat{{\theta }_b},\widehat{{\theta }_c}$…，其中之一有最小的MSE，那么这个估计量就叫做最小均方差（minimum mean square error,MMSE)估计量。如果在这些估计量中，所有的都是无偏的，其中之一有最小的方差，那么这个估计量就叫做最小方差无偏估计量(minimum variance unbiased estimator,MVUE)

估计量的选择依赖于应用情况。如果我们打算用于许多的应用，那么我们一般想要估计量是无偏的，因为一般来说我们希望估计量等于真实的值。如果我们从两个或者多个无偏估计量中选择，我们经常选择最小方差的那个。如果比较两个无偏的估计量$\widehat{{\theta }_1}$和$\widehat{{\theta }_2}$，那么其中具有相对较小的方差的那个更有效。在实际应用中，我们用它们的比值
$$\frac{var(\widehat{{\theta }_2})}{var(\widehat{{\theta }_1})}$$
它是一个衡量估计值$\widehat{{\theta }_1}$与$\widehat{{\theta }_2}$相对效率的方法。

但是，如果我们打算只应用估计值一次或者几次，那么一个（有偏差）MMSE估计值或许更有效率。在这个例子中，相对于长时间的无偏的性质，我们对与真实值的最小偏离量更感兴趣。

c) 一致估计量（Consistent Estimators) //TODO:I don’t know my translation is correct or not.

如果$\widehat{{\theta }_a}$是$\theta$的一致估计量，那么
$$P[|\widehat{{\theta }_a}-\theta |<ϵ]>(1-\delta )n>n^{\prime }$$

这里$ϵ$和$\delta$是任意小的正数，$n^{\prime }$是某个整数。我们可以将上面的等式解释为随着采样量n的增加，估计量的概率密度函数将集中与参数的真实值。当n变得非常大，估计值偏离真实值的概率将趋近于0.这种情形我们叫“$\widehat{{\theta }_a}$的概率收敛到$\theta$“。

性质a,b,c是评价估计量好与坏的理论特征。关于估计量的进一步的考虑将在参考[24]中给出。

10.14 点估计量——极大似然

一个计算估计量非常重要的技术叫做极大似然法。这个方法用途很广，例如，在生命测试中计算参数估计量。对于一般条件下的大样本数量（n趋近于无穷），极大似然技术可以得到一致估计量（consistent)、最小均值平方差估计量(MMSE)和最小方差无偏估计量(MVUE)。甚至对于中小规模的样本，极大似然技术也能产生可用的估计量。该技术基于以下的假设：从总体中抽取的特殊样本是最有可能被选择的样本。为了证明这个推论是正确的，考虑如下两个例子。

桥牌玩家不希望拿一手包含所有13张黑桃的牌。拿到这样一手牌的概率是十分小的，因为它只有一种发生的方式。但是，拿到一手黑桃的概率是和一手其他同样一张张分配好的牌的概率是一样的，因为它们也是只有一种方式。拿到一手牌的的样子可以是这样的：

• 4张黑桃
• 2张红心
• 4张方块
• 3张草花

这手牌有许多种获得的方式。准确的来说，$C_1{3}^4{C}_1{3}^2{C}_1{3}^4{C}_1{3}^3=(13{)}^4(11{)}^3(10{)}^2(3)$种方式（超过10亿）。事实上，你将会得到4-4-3-2的分布大概20%的机会。剩下的次数将会得到和这个十分类似的一手牌。极大似然技术是基于这样一个假设：我们得到的抽样是最大概率得到的那一个，或者是接近最大可能的那一个。

为了更实际的阐述，假设我们有一个特殊的摄像头来拍摄一个满是气体的箱子里的分子。当这个摄像头开发出来，我们不仅能看到分子的位置，还能看到分子的矢量速度。我们可以拍照几千年，并且它们所有的照片将看起来很类似：空间中的同类型分子向所有方向的运动。即使这样，我们依旧有概率（即使很小），我们将找到一张照片，所有的分子都在盒子的一个角落，且运动方向都是北方。如果我们应用极大似然技术到一个样本（一张给定的照片），然后我们将作出一个假设：这个样本是一个可能性，但不是非常不可能的一个。

总的来说，极大似然技术是在以下假设上发现的：我们的样本是我们从总体中抽取到的最有可能的那一个——总是带有附带条件：我们尽力确保它是随机的。

假设我们从一个根据概率密度函数(pdf) $f(x;\theta )$的总体随机抽样，这里$\theta$是一个未知的总体参数，我们想要对其进行估计。假设我们的采样（大小为n）是$x_1,x_2...x_n$，且样本的变量是独立的。利用概率密度函数，我们写下了一个表达式，该表达式给出了与特定样本相关的概率，并应用最大化的条件。

我们在区间$d{x}_1$中第一个读到是$x_1$的概率明显就是$f(x_1;\theta )d{x}_1$。在$d{x}_1$中第一个读取到的是$x_1$，并且在$d{x}_2$中第二个读到的是$x_2$的概率是
$$f(x_1;\theta )d{x}_1\dot{f}(x_2;\theta )d{x}_2$$

根据这种推理方式，我们能写出例子的概率表达式为
$$P[sample]=f(x_1;\theta )d{x}_{1}f(x_2;\theta )d{x}_{2}f(x_3;\theta )d{x}_3...f(x_n;\theta )d{x}_n\text{\hspace{1em}(X-39)}$$

如果我们抛弃微分，我们能得到一个被称作似然函数的表达式
$$\text{Likelihood Function}=f(x_1;\theta )f(x_2;\theta )...f(x_n;\theta )=\prod _{i=1}^{n}f(x_i;\theta )\text{\hspace{1em}(X-40)}$$

符号$\prod$表示连乘。似然函数在该例子中不再等于概率，但是它表示与该概率成比例的数量。（如果概率变量不独立，则似然可能会由多种分布组成，我们将试图使其最大化，具体参考[24]）

注意的是这个函数是仅仅是关于$\theta$的，因为所有的x都是已知的。我们现在将研究如何取值$\theta$，使得$L(\theta )$最大化。我们通过将其求导，让导数等于0从而得到极值条件下$\theta$的值。
$$\frac{d}{d\theta }L(\theta )=0$$
假设我们能解出该方程，将结果写作${\theta }_{M}L$，这就是极大似然估计一个未知总体的参数$\theta$。

我们现在思考一些极大似然技术在实际中的具体应用的例子。假设我们从一个总体中随机抽样，该总体符合正态分布，其均值$\mu$为未知，方差${\sigma }^2$为1。

$$f(x;\mu ,\sigma =1)=\frac{1}{\sqrt{2\pi }}exp[-\frac{(x-\mu {)}^2}{2}].$$
我们想对$\mu$做出极大似然估计。
极大似然估计的函数是

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Msijvk6t-1586708457779)(asserts/equationX_t1.png)]

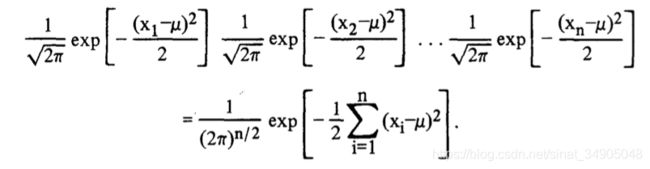
两边取自然对数，我们有

$$L(\mu )=-\frac{n}{2}ln(2\pi )-\frac{1}{2}\sum _{i=1}n(x_i-\mu {)}^2$$

应用最大化条件

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3vwfcsDM-1586708457781)(asserts/equationX_t2.png)]

这产生
$$\sum x_i-n\mu =0$$
于是
$${\mu }_{ML}=\frac{1}{n}\sum _{i=1}^n{x}_i=\overline{x}$$

因此，$\mu$的极大似然估计就是数学均值。

如果多于一个总体的参数被估计，其过程是类似的。假设在以前的例子中$\mu$和${\sigma }^2$都是未知的，那么我们的基本概率密度函数为
$$f(x;\mu ,{\sigma }^2)=\frac{1}{\sqrt{2\pi }\sigma }exp[-\frac{(x-\mu {)}^2}{2{\sigma }^2}]$$
似然函数为
$$f(x_1,\mu ,{\sigma }^2)...f(x_n;\mu ,{\sigma }^2)=\frac{1}{(2\pi {\sigma }^2{)}^{n/2}}exp[-\sum _{i=1}n\frac{(x_i-\mu {)}^2}{2{\sigma }^2}]$$

取自然对数，我们有
$$L(\mu ,{\sigma }^2)=-\frac{n}{2}ln(2\pi )-\frac{n}{2}ln{\sigma }^2-\frac{1}{2sigm{a}^2}\sum _{i=1}n(x_i-\mu {)}^2$$
我们得到$\partial L/\partial \mu$和$\partial L/[\partial ({\sigma }^2)]$并将结果等于0，第一个操作得到和以前相同的结果，也就是
$${\mu }_{M}L=\frac{1}{n}\sum _{i=1}n{x}_i=\overline{x}$$。
第二个操作得到

$${\sigma }_M^{2}L=\frac{1}{n}\sum _{i=1}n(x_i-{\overline{x}}^2)$$

这是一个${\sigma }^2$的有偏估计，其偏差可以通过将${\sigma }_M^{2}L$与数量n/(n-1)相乘来消除。那么
$${\sigma }_{unbiased}^2=\frac{1}{n-1}\sum _{i=1}n(x_i-\overline{x}{)}^2$$

如果样本的大小n比较大($n\ge 30$)，那么${\sigma }_{ML}^2$和${\sigma }_{unbiased}^2$是没什么明显的差别的。方差的估计值通常用$s^2$来表示。

作为最后一个例子，让我们返回指数分布并找到$\theta$的ML估计，也就是平均生命。//TODO：这里有点问题，ML到底如何翻译比较好？

假设我们n个部件实验中发生了n次失效，那么
$$f(t_1;\theta )...f(t_n;\theta )={\theta }^{-n}exp[-\frac{1}{\theta }\sum _{i=1}^n{t}_i]$$
且
$$L(\theta )=-nln\theta -\frac{1}{\theta }\sum _{i=1}^n{t}_i$$
因此
$$\frac{dL}{d\theta }=-\frac{n}{\theta }+\frac{1}{{\theta }^2}\sum _{i=1}n{t}_i=0$$
并且
$$\frac{1}{\theta }\sum _{i=1}^n{t}_i=n$$
于是
$${\theta }_{ML}=\frac{1}{n}\sum _{i=1}^n{t}_i$$
又一次是简单数学平均。

10.15 区间估计（Interval Estimators)

从上一节，我们学习到，基于从总体中随机抽样，如何进行总体参数的点估计。如果我们愿意，我们也可以采用一种不同的方法。这涉及到一个如下的断言(assertion)

$$P[({\hat{\theta }}_{lower}<\theta <{\hat{\theta }}_{upper})]=\eta$$

这里$\theta$是一个未知的总体参数，${\hat{\theta }}_{lower}$和${\hat{\theta }}_{upper}$是随机抽样的估计量，$\eta$是一个概率值，像是0.99，0.95什么的。假设$\eta =0.95$，我们是指如下的区间
$$({\theta }_L<\theta <{\theta }_U)$$
对于置信区间为95%情况下的${\hat{\theta }}_{lower}$和${\hat{\theta }}_{upper}$。在这个例子中，我们允许5%的概率（风险）我们的断言是错误的。

为了阐明置信区间的概念，我们用几何的方法来说明。假设我们从总体中连续的抽样$(x_1,x_2)$，它有个参数是$\theta$，我们对$\theta$设置了一个置信区间。我们在对应的纵坐标$\theta$和横坐标$x_1,x_2$中设置了三维的空间（参考X-9）。总体参数$\theta$的实际数值已被标记在了纵坐标轴上，一个横向的平面穿过了这个点。现在我们从我们95%置信区间中计算的值${\theta }_U,{\theta }_L$中随机抽样$(x_1,x_2)$。${\theta }_U$和${\theta }_L$所定义的区间被画在图中。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dDr3xUKv-1586708457782)(asserts/figureX-9.png)]

下一步我们进行第二次抽样$(x_1^{\prime },x_2^{\prime })$，据此我们在95%置信区间中计算出${\theta }_U^{\prime },{\theta }_L^{\prime }$。这个区间被标注在图中。第三次抽样$(x_1^{\prime \prime },x_2^{\prime \prime })$得到${\theta }_U^{\prime \prime },{\theta }_L^{\prime \prime }$，等等。在这种方式下，我们能生成一个大的置信区间族。这些置信区间仅仅依赖于采样的值$(x_1,x_2)(x_1^{\prime },x_2^{\prime })..$，因此我们能在不知道$\theta$的真实值的情况下计算这些区间。如果所有的置信区间都是在95%置信的基础上计算的，并且如果这些置信区间的族非常大，那么其中的95%将通过$\theta$(包含$\theta$)切割那个平面，而其中5%不会。

选择一个随机样本，并且从中计算置信区间的过程，就相当于从一个包含几千个置信区间的口袋中随机抓取一个。如果它们都是95%区间，我们选择一个包含$\theta$的机会是95%。相反的，5%的机会我们不幸的选择了一个不包含$\theta$的（就像图X-9中$({\theta }_U^{\prime \prime },{\theta }_L^{\prime \prime })$区间）。如果5%的风险感觉太高了，我们可以选择99%的区间，这个风险只有1%。如果我们选择更高的置信层次（更低的风险），如果我们持续增加置信层级，区间的长度将会增加直到100%置信，此时区间包含了每一个可能的$\theta$的值（我确信在总量10000中有缺陷的物品的数量为0至10000之间）。因此，100%置信区间没什么意义。

现在我们看一个例子，学习怎么样从一个均值为$\mu$，标准差为$\sigma$的正态分布中计算出${\theta }_L$和${\theta }_U$。在这个例子中，我们假设我们想要求解$\mu$并且已经知道$\sigma$（基于以前的数据和知识）。如果每一个样本都来自正态分布，那么样本均值$\overline{X}$是一个均值为$\mu$标准差为$\sigma /\sqrt{n}$的正态分布，这里n是样本大小。甚至如果每一个样本的值都不是取自正态分布，那么根据中心极限定理，对于一个非常大的n，$\overline{X}$也将约等同均值为$\mu$，标准差为$\sigma /\sqrt{n}$的正态分布。然后数量Z将是标准正态随机变量，这里
$$Z=\frac{\overline{X}-\mu }{\sigma /\sqrt{n}}$$
这里Z的分布已经被制表。因为Z的分布已经被制表，对于任意给定的概率$\eta$，-w和w的值，这样
$$P[-w<Z\le w]=\eta$$
例如，对于$\eta =0.95,w=1.96$。上式中取代Z，我们有
$$P[-w\le \frac{\overline{X}-\mu }{\sigma /\sqrt{n}}\le w]=\eta$$
这里w对于任意给定的$\eta$是已知的。(例如，我们可以替代$\eta$为0.95且w为1.96)

下面我们来专注于最后一个公式左边的不等式，并将它转化成如下的形式：
$$[{\theta }_L<\mu <{\theta }_U]$$
各项都乘以因子$\sigma /\sqrt{n}$，将不等式转换成
$$[-w\frac{\sigma }{\sqrt{n}}<\overline{X}-\mu <+w\frac{\sigma }{\sqrt{n}}]$$
每一项减去$\overline{X}$
$$[-w\frac{\sigma }{\sqrt{n}}-\overline{X}<-\mu <w\frac{\sigma }{\sqrt{n}}-\overline{X}]$$
下一步我们将每一项乘以-1，注意此操作要将不等式反向。
$$[w\frac{\sigma }{\sqrt{n}}+\overline{X}>\mu >-w\frac{\sigma }{\sqrt{n}}+\overline{X}]$$
我们可以写成如下的形式
$$[\overline{X}-w\frac{\sigma }{\sqrt{n}}<\mu <\overline{X}+w\frac{\sigma }{\sqrt{n}}]$$
该不等式得出了$\mu$的置信区间，在总体均值的情况下，那么
$$\begin{gathered} {\theta }_L=\overline{x}-w\frac{\sigma }{\sqrt{n}} \\ {\theta }_U=\overline{x}+w\frac{\sigma }{\sqrt{n}} \end{gathered}$$

如果给定了置信系数$\eta$，$\overline{x},n,w$是已知的。$\sigma$的值假设也已经知道。如果我们不知道$\sigma$的值，从先前的正态分布描述中，我们可以通过采样来估计$\sigma$，从而获得数量s。现在我们可以形成标准值t，其中
$$t=$$