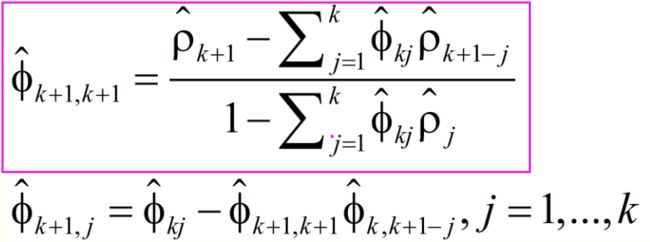计量经济与时间序列_ACF自相关与PACF偏自相关算法解析(Python,TB(交易开拓者))

1   在时间序列中ACF图和PACF图是非常重要的两个概念，如果运用时间序列做建模、交易或者预测的话。这两个概念是必须的。

2   ACF和PACF分别为：自相关函数(系数)和偏自相关函数(系数)。

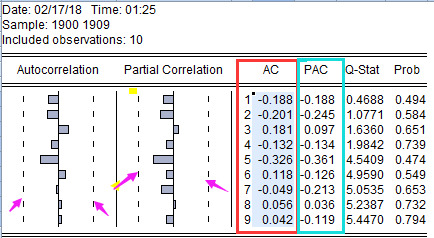
3   在许多软件中比如Eviews分析软件可以调出某一个序列的ACF图和PACF图，如下：

　　

　　3.1   有时候这张图是横躺着的，不过这个不重要，反正一侧为小于0的负值范围，一侧为大于0的正值范围，均值（准确的说是坐标y轴为0，有些横着的图，会把x轴和y轴表示出来，值都在x轴上下附近呈现出来）。

　　3.2   红色框框部分就是ACF图，青色框框部分就是PACF图，其中对应左边的Autocorrelation就是英文单词自相关的全称；Partial Correlation就是英文单词偏自相关的全称。

　　3.3   我们要计算的就是这两列数值。

　　3.4   其中紫色箭头标注出来的是指的2倍标准误范围，后面可以用对应的数值是否超过范围来判断截尾、拖尾等信息，进而判断采用哪种模型。

　　3.5   这里特别注明一下在默认状态下，这两根线是如何计算的：

　　　　在大样本下（T很大的时候，这里T指的是样本的个数；其实准确的说样本符合均值为0的正太分布）。因此这里的对于ACF或PACF属于一种分位点检验，这个东西在很多baidu可以找到一个正太分布图，然后左右画线会得到99%，90%...的分位点，这里的这两根线就是指的这个。我们这里要做的是双侧对称检验，所以上下两根线分布式0±分位点的值。分位点=2倍×sqrt开方(1/T)，这里的T指的是样本的个数，样本个数指的是原始的那个样本的个数，不是ACF或PACF计算完的样本个数。如果某一个值大于2倍标准误，也就是说大于正态分布左/右的95%分位点，于是，在拒绝域，则拒绝0假设（也就是拒绝均值为0的假设）

　　　　例如：样本共10个，ACF或PACF计算完毕后，他们的数量都为9个，其分为点为：2×sqrt(1/10) = 0.6324555320...，双侧检验边沿值为：(0-0.6324555320,0+0.6324555320) = [-0.6324555320,+0.6324555320]（这就是两根虚线的值）。　　　　(3.5.1)

　　　　　　　另外我们还通过另外一个公式Sρk ≈ sqrt(1/n * (1+2*ρ₁² + ... + 2*ρ_k-1²))来计算acf的双侧检验值。具体在这篇博文中得出。http://www.cnblogs.com/noah0532/p/8453959.html

 

4    ACF算法的实现（python）：

　　4.1   首先：给定一组数据，这里的是线性数据，不用太多10个元素，一组的时间序列。

1 TimeSeries = [13, 8, 15, 4, 4, 12, 11, 7, 14, 12]  # 列表形式
2 print(TimeSeries)
3 # 显示结果：[13, 8, 15, 4, 4, 12, 11, 7, 14, 12]

　　4.2   算法表达式。

　　

　　4.3   算法解析：

　　计算ρ1：

　　给定一阶滞后序列：其中滞后用L来表示，具体表示方法见链接：http://www.cnblogs.com/noah0532/p/8449991.html

1 LZt = TimeSeries[:-1:]
2 print(LZt)
3 # 显示结果：[13, 8, 15, 4, 4, 12, 11, 7, 14]

　　对应的这两个序列分别为：

　　[13, 8, 15, 4, 4, 12, 11, 7, 14, 12]
　　[13, 8, 15, 4, 4, 12, 11, 7, 14]

　　我们在把原始序列与一阶滞后序列进行对齐：

1 Zt = TimeSeries[1::]
2 print(Zt)
3 # 显示结果：[8, 15, 4, 4, 12, 11, 7, 14, 12]

　　这样两个序列变为：

　　[ 8, 15, 4, 4, 12, 11, 7, 14, 12]
　　[13, 8, 15, 4, 4, 12, 11, 7, 14]　　

　　对这两个序列进行计算就会得出ρ1的结果（也就是ACF的第一个值）

　　4.4   其实我们可以得到这样一个结果，就是这样不断的比较下去，计算每一个滞后，原始序列会少一个值来对应滞后的序列，然后分别来进行计算。我们把这个过程化简一下，代码如下（以如上10个序列为例，最后会得出9对）

 1 TimeSeries = [13, 8, 15, 4, 4, 12, 11, 7, 14, 12]  # 列表形式
 2 Zt = []
 3 LZt = []
 4 i = 1
 5 while i < len(TimeSeries):
 6     L = TimeSeries[i::]
 7     LL = TimeSeries[:-i:]
 8     Zt.append(L)
 9     LZt.append(LL)
10     i += 1
11 print(TimeSeries)
12 print(Zt)
13 print(LZt)
14 # 显示结果：
15 # [13, 8, 15, 4, 4, 12, 11, 7, 14, 12]
16 # [[8, 15, 4, 4, 12, 11, 7, 14, 12], [15, 4, 4, 12, 11, 7, 14, 12], [4, 4, 12, 11, 7, 14, 12], [4, 12, 11, 7, 14, 12], [12, 11, 7, 14, 12], [11, 7, 14, 12], [7, 14, 12], [14, 12], [12]]
17 # [[13, 8, 15, 4, 4, 12, 11, 7, 14], [13, 8, 15, 4, 4, 12, 11, 7], [13, 8, 15, 4, 4, 12, 11], [13, 8, 15, 4, 4, 12], [13, 8, 15, 4, 4], [13, 8, 15, 4], [13, 8, 15], [13, 8], [13]]

　　4.5   通过这种遍历加减方式，如果原始列表为10个元素的话会得到9对ACF带计算序列，以此类推，这样做的目的就是为了把序列进行对齐计算。把这9对列出来看一下：

　　[8, 15, 4, 4, 12, 11, 7, 14, 12]
　　[13, 8, 15, 4, 4, 12, 11, 7, 14]

　　[15, 4, 4, 12, 11, 7, 14, 12]
　　[13, 8, 15, 4, 4, 12, 11, 7]

　　[4, 4, 12, 11, 7, 14, 12]
　　[13, 8, 15, 4, 4, 12, 11]

　　[4, 12, 11, 7, 14, 12]
　　[13, 8, 15, 4, 4, 12]

　　[12, 11, 7, 14, 12]
　　[13, 8, 15, 4, 4]

　　[11, 7, 14, 12]
　　[13, 8, 15, 4]

　　[7, 14, 12]
　　[13, 8, 15]

　　[14, 12]
　　[13, 8]

　　[12]
　　[13]

 　　4.6   根据算法公式，其分母为原始序列每一个元素距离平均值的平方。因此我们也可以把分母计算出来。

 1 TimeSeries = [13, 8, 15, 4, 4, 12, 11, 7, 14, 12]  # 列表形式
 2 Zt = []
 3 LZt = []
 4 sum = 0
 5 i = 1
 6 while i < len(TimeSeries):
 7     L = TimeSeries[i::]
 8     LL = TimeSeries[:-i:]
 9     sum = sum + TimeSeries[i - 1]
10     Zt.append(L)
11     LZt.append(LL)
12     i += 1
13 sum = sum + TimeSeries[-1]
14 avg = sum / len(TimeSeries)
15 print(TimeSeries)
16 print(Zt)
17 print(LZt)
18 print(avg)
19 # 显示结果：
20 # 10.0

　　4.7   我们具备了这些所有的元素后开始计算这些所有ACF的ρ值，最终我们还是用列表来表示：

 1 k = 0
 2 result_Deno = 0
 3 # 首先计算分母=分母都为通用
 4 while k < len(TimeSeries):
 5     result_Deno = result_Deno + pow((TimeSeries[k] - avg), 2)
 6     k += 1
 7 print(result_Deno)
 8 # 显示结果：144.0
 9 
10 # 然后计算分子
11 p = 0
12 q = 0
13 14 acf = []
15 while p < len(Zt):
16     # print(Zt[p])
17     # print(LZt[p])
18     q = 0
19     result_Mole = 0
20     while q < len(Zt[p]):
21         result_Mole = result_Mole + (Zt[p][q] - avg) * (LZt[p][q] - avg)
22         q += 1
23     acf.append(round(result_Mole / result_Deno, 3))  # 保留小数点后三位
24     p += 1
25 print(acf)
26 # 显示结果：
27 # [-0.188, -0.201, 0.181, -0.132, -0.326, 0.118, -0.049, 0.056, 0.042]

　　4.7   结果验证：与用Eviews软件计算的结果一致，算法结束：

[-0.188, -0.201, 0.181, -0.132, -0.326, 0.118, -0.049, 0.056, 0.042]

 

5   PACF算法的实现（python）

 　  5.1   PACF算法源于ACF算法，必须先算出ACF的值来，然后再计算PACF，PACF这里用的是一个递推形式的公式，计算每一个φ值。在书中有些φ值用φ_kk来表示，有时候也用一个大Pk来表示，其实道理都一样。

　　5.2   递推式如下：

　　5.3   这个递推式，紫色框内为每期值，下面的属于过度值，用于递推累计。

　　5.4   这个递推式算法看起来无从下手比较麻烦。我们先分解一下：

　　5.5   j和k的下标解析：

　　　　如果k = 1，那么 j = 1,2

　　　　如果k = 2，那么 j = 1,2

　　　　如果k = 3，那么 j = 1,2,3

　　　　如果k = 4，那么 j = 1,2,3,4

　　　　如果k = 5，那么 j = 1,2,3,4,5

　　　　如果k = 6，那么 j = 1,2,3,4,5,6

　　　　如果k = 7，那么 j = 1,2,3,4,5,6,7

　　　　如果k = 8，那么 j = 1,2,3,4,5,6,7,8

　　　　如果k = 9，那么 j = 1,2,3,4,5,6,7,8,9

　　　　... ....

　　　　从下标可以看出这个递推关系，如果处于k的某种状态（数值），那么 j 将从当前状态递减到1。这也就是 j = 1,...,k的解析。

　　5.6   从这个下标解析可以看出，这两部分的递推式，第一部分（紫色框框中）的是计算PACF当前值，而第二部分是计算每阶段的PACF值的缺省值（所需值）的计算。因此每期的PACF值的计算，需要递推第二个公式中的值，然后再去计算下一期PACF值。这个逻辑是这样。

　　5.7   从5.5的这个规律可以看出，j 是 k递减数，也就是当前值如果为k = 3的话，我们需要有3个第二个公式的值；如果k = 7的话，我们需要有7个第二个公式的值；这个逻辑是没有问题的，我们以一个多的为例子

　　　　k = 8 通式如下：

　　　　φ_9,j = φ_8j - φ₉₉*φ_8,9-j

　　　　j = 1

　　　　φ₉₁ = φ₈₁ - φ₉₉*φ₈₈

　　　　j = 2

　　　　φ₉₂ = φ₈₂ - φ₉₉*φ₈₇

　　　　j = 3

　　　　φ₉₃ = φ₈₃ - φ₉₉*φ₈₆

　　　　j = 4

　　　　φ₉₄ = φ₈₄ - φ₉₉*φ₈₅

　　　　j = 5

　　　　φ₉₅ = φ₈₅ - φ₉₉*φ₈₄

　　　　j = 6

　　　　φ₉₆ = φ₈₆ - φ₉₉*φ₈₃

　　　　j = 7

　　　　φ₉₇ = φ₈₇ - φ₉₉*φ₈₂

　　　　j = 8

　　　　φ₉₈ = φ₈₈ - φ₉₉*φ₈₁

 　　5.8   正如上面所示，我们会得到8个表达式。其每一期的表达式的值我们需要用列表来进行记录；这里的规律是φ99来自于第一个部分的公式，其φ8x和后面的φ8x是来自第二部分公式计算的上一期的值。这样这个第二部分的表达式我们就可以计算出来了。

　　 5.9   我们再来递推第一部分的那个公式。还是以上面的为例子。我们举一个小点儿的数。

　　　　k = 2   通式如下

　　　　φ₃₃ = φ₃ - sigma(φ_2j*ρ_3-j) / 1 - sigma(φ_2j*ρ_j)

　　　　j = 1

　　　　φ₃₃ = φ₃ - sigma(φ₂₁*ρ₂) / 1 - sigma(φ₂₁*ρ₁)

　　　　j = 2

　　　　φ₃₃ = φ₃ - sigma(φ₂₂*ρ₁) / 1 - sigma(φ₂₂*ρ₂)

　　　　我们把sigma中的两部分进行合并得：

　　　　φ₃₃ = φ₃ - (φ₂₁*ρ₂ +  φ₂₂*ρ₁) / 1 - (φ₂₁*ρ₁ + φ₂₂*ρ₂)

 　　5.10   我们发现一个规律。如果要计算33的时候，其括号内的值φ的顺序不变，其ρ值为反向求积然后再求和。

　　 5.11   我们现在试着来求一下这段代码的写法，以上面计算出来的ACF值，接着来计算PACF值：

　　ACF = [-0.188, -0.201, 0.181, -0.132, -0.326, 0.118, -0.049, 0.056, 0.042]

　　ACF[0] = ρ₁ = -0.188

　　ACF[1] = ρ₂ = -0.201

　　ACF[2] = ρ₄ = 0.181

　　ACF[3] = ρ₅ = -0.132

　　ACF[4] = ρ₆ = -0.326

　　ACF[5] = ρ₇ = 0.118

　　ACF[6] = ρ₈ = -0.049

　　ACF[7] = ρ₉ = 0.056

　　ACF[8] = ρ₉ = 0.042

　　5.12   （具体过程稍显复杂，所以下面用这个颜色写，这样更清楚一些）：

　　　　(1)：递推算法，在编写的时候可能会对初学者烧脑一些。重要的是对于每一种算法，我们首先要找到他们的规律，再不会算，可以找张纸先手工验算一下。

　　　　(2)：acf值与pacf值的长度都是一样，且第一个值都相等。φ_kk如果是两个整数，比如φ₁₁，φ₃₃，这就是我们要求的pacf对应每期的值。

　　　　(3)：正如上面所说的，都是整数的话是所求的值，那么不是整数的话，类似于φ₄₁，φ₄₂，φ₄₃...等等这些，就是第二个递推式所需要计算的值。这是值是为了求下一组数值所用。

　　　　(4)：因此我们得出这样一个规律，除去第一个值（pacf和acf第一个值都相等）。后面每期值分两组来进行计算，然后一组循环结束，以此类推，知道pacf长度减-1都完成为止。

　　　　(5)：那么一组是什么样子的？比如第一组是：φ₂₂，φ₂₁；第二组：φ₃₃，φ₃₂，φ₃₁；第三组：φ₄₄，φ₄₃，φ₄₂，φ₄₁...以此类推。一组等于一个大循环。

　　　　(6)：每组值分第一部分整值计算和第二部分非整值计算，每一组所需的φ值（看递推公式），是来自于上一组的值。因此我们计算完一组后，把所需要的值（代码中是用个过渡变量bridge来记录），送给下一组计算用，计算完毕删除，再赋新值，再给下一组。循环往复，直到结束。

　　　　(7)：那每组需要的值是什么样子，以计算到φ₄₄,这个为例子，所需要的bridge值为[φ₃₁，φ₃₂，φ₃₃]。用完了后，bridge更新为[φ₄₁，φ₄₂，φ₄₃，φ₄₄]，供下一组φ₅₅使用，其他每组都是这个原理。在这里引入了一个桥变量。

　　　　(8)：由于精度可能略有差别，这样我们把之前计算的acf值先不要保留小数点后三位，计算完毕后，我们统一保留小数点后三位。

　　　　(9)：最后再把上边界和下边界的值算出来。这个公式上面有。

　　5.13   具体代码如下：

  1 TimeSeries = [13, 8, 15, 4, 4, 12, 11, 7, 14, 12]  # 列表形式
  2 Zt = []
  3 LZt = []
  4 total = 0
  5 i = 1
  6 while i < len(TimeSeries):
  7     L = TimeSeries[i::]
  8     LL = TimeSeries[:-i:]
  9     total = total + TimeSeries[i-1]
 10     Zt.append(L)
 11     LZt.append(LL)
 12     i += 1
 13 total = total + TimeSeries[-1]
 14 avg = total / len(TimeSeries)
 15 
 16 k = 0
 17 result_Deno = 0
 18 # 首先计算分母=分母都为通用
 19 while k < len(TimeSeries):
 20     result_Deno = result_Deno + pow((TimeSeries[k] - avg), 2)
 21     k += 1
 22 # print(result_Deno)
 23 # 显示结果：144.0
 24 
 25 # 然后计算分子
 26 p = 0
 27 q = 0
 28 acf = []
 29 while p < len(Zt):
 30     # print(Zt[p])
 31     # print(LZt[p])
 32     q = 0
 33     result_Mole = 0
 34     while q < len(Zt[p]):
 35         result_Mole = result_Mole + (Zt[p][q] - avg) * (LZt[p][q] - avg)
 36         q += 1
 37     acf.append(result_Mole / result_Deno)  # 我们把前面计算的acf值先不要保留小数点后三位。
 38     # acf.append(result_Mole / result_Deno)
 39     p += 1
 40 # print(acf)
 41 
 42 # 初始化pacf
 43 pacf = []
 44 bridge = []
 45 bridge.append(acf[0])
 46 pacf.append(acf[0])   # 第一个φ11等于ρ1，再初始化pacf的第一个值。
 47 # 这里采用的是bridge这个循环变量。计算的逻辑是每次重新赋值一遍共下一轮计算所用。
 48 
 49 
 50 T = 0  # 初始化大循环的值为0，9个数值一共循环7次。原因是下面。
 51 while T < len(acf)-1:   # pacf的初始值已经计算过一个了，acf的长度和pacf的长度是一样的，因此，len(acf)此时要减去一个1
 52     # 每进行一轮循环，这些变量都重新初始化一遍
 53     Mole = 0 # 计算紫框中Σ累加的分子值
 54     Deno = 0 # 计算紫框中Σ累计的分母值
 55     cross = 0 # 每计算完一遍第一部分的值，暂时用cross这个变量先保存起来。
 56     UnderCross = [] # 每计算完第二步的值，用UnderCross的值先保存起来，因为有时候第二步的值不是一个，所以用列表形式。
 57 
 58     # 计算第一部分
 59     t = 0
 60     while t < len(bridge):    # 计算φ22，φ33，φ44，φ55，φ66，φ22，φ77，φ88...这些值
 61         Mole = Mole + (bridge[t] * acf[len(bridge)-1-t])
 62         Deno = Deno + (bridge[t] * acf[t])
 63         t += 1
 64     cross = (acf[t] - Mole) / (1 - Deno)  # acf[t] 正确，每次迭代完成，都是分子的第一个值。
 65     # print(cross)
 66     # print(t)
 67 
 68     # 计算第二部分
 69     p = 0
 70     while p < len(bridge):   # 计算像φ21，φ32，φ31...这样的值
 71         UnderCross.append(bridge[p] - cross * bridge[len(bridge)-1-p])
 72         p += 1
 73 
 74     bridge = []  # bridge使用完毕，初始化，再次赋值供下一次计算
 75     bridge.extend(UnderCross)   # 把计算完毕的Under值赋值到bridge
 76     bridge.append(cross)   # 把计算完毕的cross值存放到最后的位置
 77     pacf.append(cross)   # 把pacf值累计进行添加并记录
 78     # print(bridge)
 79     # print(UnderCross)
 80 
 81     T += 1
 82 # print(pacf)
 83 # 整个的一段循环完毕。
 84 
 85 
 86 # 最后我们重新遍历一遍，然后把acf和pacf都保留小数点后三位。
 87 AcfValue = []
 88 PacfValue = []
 89 lag = 0
 90 for sht in acf:
 91     lag = round(sht, 3)
 92     AcfValue.append(lag)
 93     lag = 0
 94 print("acf值(保留小数点后三位)为：", AcfValue)
 95 
 96 for sht in pacf:
 97     lag = round(sht, 3)
 98     PacfValue.append(lag)
 99     lag = 0
100 print("pacf值(保留小数点后三位)为：", PacfValue)
101 
102 
103 # 最后把bounds值算出来。
104 import math
105 bound = []
106 bound.append(-2*math.sqrt(1/len(TimeSeries)))
107 bound.append(2*math.sqrt(1/len(TimeSeries)))
108 print("上下边界值分别为：", bound)
109 
110 # 最终显示结果：
111 # acf值(保留小数点后三位)为： [-0.188, -0.201, 0.181, -0.132, -0.326, 0.118, -0.049, 0.056, 0.042]
112 # pacf值(保留小数点后三位)为： [-0.188, -0.245, 0.097, -0.134, -0.361, -0.126, -0.213, 0.036, -0.119]
113 # 上下边界值分别为： [-0.6324555320336759, 0.6324555320336759]

　　5.14   最终结果验证：

acf值(保留小数点后三位)为： [-0.188, -0.201, 0.181, -0.132, -0.326, 0.118, -0.049, 0.056, 0.042]
pacf值(保留小数点后三位)为： [-0.188, -0.245, 0.097, -0.134, -0.361, -0.126, -0.213, 0.036, -0.119]
上下边界值分别为： [-0.6324555320336759, 0.6324555320336759]这里是计算的pacf的bound值。在看图的时候直接通用pacf的bound值。但是实际过程中这两个标准差是不太一样。具体见这篇博文http://www.cnblogs.com/noah0532/p/8453959.html

　　对照上面给出的Eviews软件自动统计的值：

　　结果完全一致！　　

 6   TB（交易开拓者代码）

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

（持续编辑中。。。。。。。。。。）

 

转载于:https://www.cnblogs.com/noah0532/p/8451375.html