常见组合逻辑电路
目录
- 三裁判表决电路
-
- 真值表方式
- 逻辑代数方式
- 结构描述方法
- 逻辑代数方式
- 数字加法器
-
- 全加器
- 超前进位加法器
- 数据比较器
- 数据选择器
-
- 结构级描述方式
- 抽象描述方式
- 数字编码器
-
- 3位二进制8-3编码器
- 8-3优先编码器
- 数字译码器
- 奇偶校验器
组合电路的特点是,电路中任意时刻的稳态输出仅仅取决于该时刻的输入,而与电路原来的状态无关。组合电路没有记忆功能,只有从输入到输出的通路,没有从输出到输入的回路。
组合电路的描述方式主要有四种:真值表、逻辑代数、结构描述以及抽象描述。
三裁判表决电路
我们以三裁判表决电路来举例说明这四种描述方式。
设计一个3个裁判的表决电路,当两个或两个以上裁判同意时,判决器输出“1”,否则输出“0”。
真值表方式
真值表如下所示:
| A | B | C | OUT |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
代码如下:
module design1 (OUT, A, B, C); //真值表形式
output OUT;
input A, B, C;
reg OUT;
always @(A or B or C)
case({A, B, C})
3'b000:OUT <= 0;
3'b001:OUT <= 0;
3'b010:OUT <= 0;
3'b100:OUT <= 0;
3'b011:OUT <= 1;
3'b101:OUT <= 1;
3'b110:OUT <= 1;
3'b111:OUT <= 1;
endcase
endmodule
真值表描述方式实质上是最小项表达式,该描述方式设计的电路结构如下所示:
逻辑代数方式
将真值表用卡诺图来表示,然后化简电路,得出逻辑表达式。卡诺图如下:

通过对卡诺图的化简,可以得到组合电路逻辑输出与输入之间的逻辑函数表达式:
OUT = AB + BC +AC
代码如下:
module design2 (OUT, A, B, C);
output OUT;
input A, B, C;
assign OUT = (A&B)|(B&C)|(A&C); //OUT = AB + BC + AC
结构描述方法
module design3 (OUT, A, B, C);
output OUT;
input A, B, C;
and U1(w1, A, B);
and U2(w2, B, C);
and U3(w3, A, C);
or U4(OUT, w1, w2, w3);
endmodule
逻辑代数方式
直接从电路功能出发,编写代码。
例如,对于这个判决器,将三个输入的判决相加,当判决成功的时候相加器之和大于1,及表示投票成功,代码如下:
module desing4 (OUT, A, B, C);
output OUT;
input A, B, C;
wire [1:0]sum;
reg OUT;
assign sum = A + B + C;
always @(sum)
if (sum > 1) OUT = 1;
else OUT = 0;
endmodule
数字加法器
广义的加法器包括加法器和减法器,就电路结构而言,加法电路和减法电路是一样的,只不过输入信号采用的是补码输入。
全加器
如果运算考虑了来自低位的进位,那么该运算就为全加运算。2输入1bit信号全加器的真值表如下所示:
| A | B | C_IN | SUM | C_OUT |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
- 利用连续赋值语句实现:
module one_bit_fulladder1 (SUM, C_OUT, A, B, C_IN); //连续赋值语句实现
input A, B, C_IN;
output SUM. C_OUT;
assign SUM = (A^B)^C_IN;
assign C_OUT = (A&B)|(B&C)|(A&C);
endmodule
- 利用行为描述方式实现:
module one_bit_fulladder2 (SUM, C_OUT, A, B, C_IN); //行为描述方式实现
input A, B, C_IN;
output SUM, C_OUT;
assign {C_OUT, SUM} = A + B + C_IN;
endmodule
采用行为描述方式可以提高设计的效率,对于一个典型的多位加法器的行为描述设计,仅需要改变代码中输入和输出信号的位宽即可。例如一个2输入8bit加法器,可以采用下面的代码来实现:
module eight_bit_fulladder (SUM, C_OUT, A, B, C_IN);
input[7:0] A,B;
input C_IN;
output[7:0] SUM;
output C_out;
assign{C_OUT, SUM} = A + B + C_IN;
endmodule
超前进位加法器
超前进位加法器的每级进位由附加的组合电路产生,高位的运算不需等待低位运算完成,因此可以提高运算速度。
对于一个4位超前进位加法器,其各级信号表达式为:
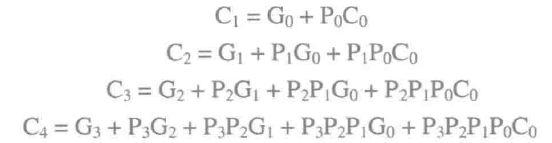
电路如下:

代码如下:
module four_bit_fast_adder (sum_out, c_out, a, b, c_in);
input[3:0] a,b; //加数,被加数
input c_in; //来自前级的进位
output[3:0] sum_out; //和
output c_out; //进位输出
wire[4:0] g, p, c; //产生函数、传输函数和内部进位
assign c[0] = c_in;
assign p = a|b;
assign g = a&b;
assign c[1] = g[0]|(p[0]&c[0]);
assign c[2] = g[1]|(p[1]&(g[0]|(p[0]&c[0])));
assign c[3] = g[2]|(p[2]&(g[1]|(p[1]&(g[0]|(p[0]&c[0])))))
assign c[4] = g[3]|(p[3]&(g[2]|(p[2]&(g[1]|(p[1]&(g[0]|(p[0]&c[0])))))))
assign sum_out = p^c[3:0];
assign c_out = c[4];
endmodule
数据比较器
数据比较器用来对两个二进制数的大小进行比较,或检测逻辑电路是否相等。数据比较器包含两部分功能:比较两个数的大小,检测两个数是否一致。
多位数据比较器的比较过程由高位到低位逐位进行,而且只有在高位相等时,才进行低位比较。以4位数据比较器为例,在进行A3、A2、A1、A0和B3、B2、B1、B0的比较时,首先比较最高位A3和B3,如果A3>B3,那么不管其他几位数为何值,结果均为A>B;若A3

用F[2:0]表示比较结果,C[2:0]表示前一级比较结果,代码如下:
module four_bits_comp1 (F, A, B, C);
parameter comp_width = 4;
output [2:0]F;
input [2:0]C;
input [comp_width-1:0]A;
input [comp_width-1:0]B;
reg [2:0]F;
always @(A or B or C)
if (A > B) F = 3'b100;
else if (A < B) F = 3'b001;
else F = C;
endmodule
数据选择器
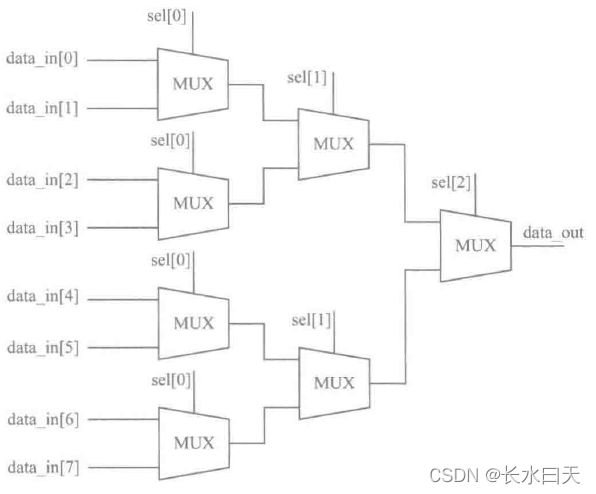
数据选择器又称多路选择器(MUX),它有n位地址输入、2的n次方位数据输入、1位数据输出。每次在输入地址的控制下,从多路输入数据中选择一路输出,其功能类似于一个单刀多掷开关:

以8选1数据选择器为例,其可以由多个2选1数据选择器构成,也可以采用抽象描述方式进行设计。
结构级描述方式
module mux8to1_1 (d_out, d_in, sel);
output d_out;
input [7:0] d_in;
input [2:0] sel;
wire [3:0] w1;
wire [1:0] w2;
assign w1 = sel[0]?{d_in[7], d_in[5], d_in[3], d_in[1]}:{d_in[6], d_in[4], d_in[2], d_in[0]};
//选奇偶
assign w2 = sel[1]?{w1[3], w1[1]}:{w1[2], w1[0]};
assign d_out = sel[2]?w2[1]:w2[0];
endmodule
抽象描述方式
采用case语句直接进行设计,在这种方式中,只需考虑选择信号列表就可以实现功能更为复杂的数据选择器。
module mux8to1_2 (out, sel, data_in);
output out;
input [7:0]data_in;
input [3:0]sel;
reg out;
always @(data_in or sel)
case (sel)
3'b000:out <= data_in[0];
3'b001:out <= data_in[1];
3'b010:out <= data_in[2];
3'b011:out <= data_in[3];
3'b100:out <= data_in[4];
3'b101:out <= data_in[5];
3'b110:out <= data_in[6];
3'b111:out <= data_in[7];
endcase
endmodule
数字编码器
用文字、符号或数码表示特定对象的过程称为编码。在数字电路中用二进制代码表示有关的信号称为二进制编码、实现编码操作的电路叫做编码器。
3位二进制8-3编码器
用n位二进制代码对N = 2的n次方个一般信号进行编码的电路叫做二进制编码器。例如n=3,可以对8个一般信号进行编码。这种编码器的特点是:任何时刻只允许输入一个有效信号,不允许同时出现两个或两个以上的有效信号。假设编码器规定高电平为有效电平,则在任何时刻只有一个输入端为高电平,其余输入端为低电平。
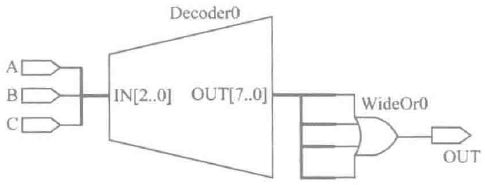
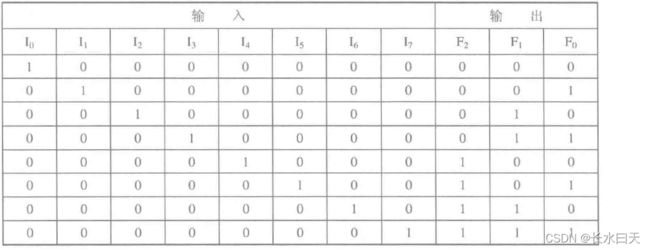
下图是3位二进制8-3编码器示意图,它的输入为I0~I7,8个高电平有效信号,输出是3位二进制代码F2、F1、F0。

输出与输入的对应关系如下所示:
采用抽象描述方式的代码如下:
module code_8to3 (F, I);
output [2:0]F;
input [7:0]I;
reg [2:0]F;
always @(I)
case(I)
8'b00000001:F = 3'b000;
8'b00000010:F = 3'b001;
8'b00000100:F = 3'b010;
8'b00001000:F = 3'b011;
8'b00010000:F = 3'b100;
8'b00100000:F = 3'b101;
8'b01000000:F = 3'b110;
8'b10000000:F = 3'b111;
default:F = 3'bx;
endcase
endmodule
8-3优先编码器
优先编码器允许多个输入信号同时有效,但是它只对其中优先级别最高的有效输入信号编码,对级别低的信号不予理睬。8-3优先编码器逻辑符号如下:

他有8个输入端I0—I7,低电平为输入有效电平;3个输出端Y0~Y2,低电平为输出有效电平。此外,为了便于电路的扩展和使用的灵活,还设置有使能端S、选通输出端Ys和扩展端Yex。
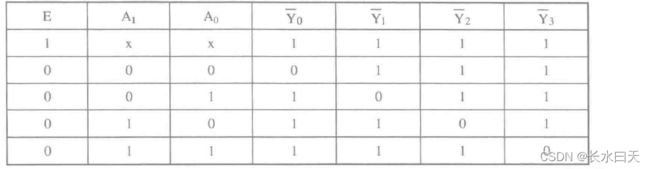
真值表如下:

- S=1时,电路处于禁止工作状态,此时无论8个输入为何种状态,3个输出端均为高电平,Ys和Yex也为高电平,编码器不工作。
- S=0时,电路处于正常工作状态,允许I0~I7当中有几个输入端为低电平,即同时有几路编码输入信号有效。在8个输入端中,I7的优先级最高,I0的优先权最低。当I7=0时,无论其他输入端有否有效输入信号(功能表中以X表示),输出端只输出I7的编码,即Y2Y1Y0 =000。
- 表中出现的三种Y2Y1Y0 =111的情况可以用Ys和Yex的不同状态来区别,即如果Y2Y1Y0 =111且YsYex=10,则表示电路处于工作状态而且I0有编码信号输入;如果Y2Y1Y0 =111且YsYex=01,则表示电路处于工作状态但没有输入编码信号。
具体代码如下:
module mux8to3_p (data_out, Ys, Yex, sel, data_in);
output [2:0] data_out;
output Ys, Yex;
input [7:0] data_in;
input sel;
reg [2:0] data_out;
reg Ys, Yex;
always @(data_in or sel)
if (sel) {data_out, Ys, Yex} = {3'b111, 1'b1, 1'b1};
else
begin
casex (data_in)
8'b0???????:{data_out, Ys, Yex} = {3'b000, 1'b1, 1'b0};
8'b10??????:{data_out, Ys, Yex} = {3'b001, 1'b1, 1'b0};
8'b110?????:{data_out, Ys, Yex} = {3'b010, 1'b1, 1'b0};
8'b1110????:{data_out, Ys, Yex} = {3'b011, 1'b1, 1'b0};
8'b11110???:{data_out, Ys, Yex} = {3'b100, 1'b1, 1'b0};
8'b111110??:{data_out, Ys, Yex} = {3'b101, 1'b1, 1'b0};
8'b1111110?:{data_out, Ys, Yex} = {3'b110, 1'b1, 1'b0};
8'b11111110:{data_out, Ys, Yex} = {3'b111, 1'b1, 1'b0};
8'b11111111:{data_out, Ys, Yex} = {3'b111, 1'b1, 1'b0};
endcase
end
endmodule
数字译码器
译码是编码的逆过程,它将二进制代码所表示的信息翻译成相应的状态信息,实现译码功能的电路称为译码器。
N位二进制译码器有N个输入端和2的N次方个输出端,。
以2-4译码器为例,逻辑电路如下:

A1、A0为地址输入端,A1为高位。Y0、Y1、Y2、Y3为状态信号输出端,低电平有效,E为使能端,低电平有效。
- 当E=0时,允许译码器工作,Y0~Y3中只允许一个为有效电平输出。
- 当E=1时,禁止译码器工作,所有输出Y0~Y3均为高电平。
- 一般使能端有两个用途,一是引入选通脉冲,以抑制冒险脉冲的发生;二是用来扩展输入的变量数(功能扩展)。
module decode_2to4_1 (Y, E, A);
output [3:0] Y;
input [1:0] A;
input E;
assign Y[0] = ~(~E&~A[1]&~A[0]);
assign Y[1] = ~(~E&~A[1]&A[0]);
assign Y[2] = ~(~E&~A[1]&~A[0]);
assign Y[3] = ~(~E&A[1]&A[0]);
endmodule
采用抽象描述方式进行设计的电路代码如下:
module decode_2to4_2 (Y, E, A);
output [3:0] Y;
input [1:0] A;
input E;
reg [3:0] Y;
always @(E or A)
case({E, A})
3'b1?? : Y = 4'b0000;
3'b000 : Y = 4'b0001;
3'b001 : Y = 4'b0010;
3'b010 : Y = 4'b0100;
3'b011 : Y = 4'b1000;
default : Y = 4'b0000;
endcase
endmodule
奇偶校验器
- 奇偶校验器的功能是检测数据中所含“1”的个数是奇数还是偶数。
- 奇偶校验包含两种方式:奇校验和偶校验。奇校验保证传输数据和校验位中“1”的总数为奇数。如果数据中包含奇数个“1”,则校验位置为0,如果包含偶数个“1”,则校验位置为1.偶校验则相反,包含偶数个“1”时,校验位置为0。
- 奇偶校验只能检测部分传输错误,不能确定错误发生在哪位或哪几位,所以不能进行错误校正。当数据发生错误时只能重新发送数据。
以8bit奇偶校验器为例,原理如下:

校验器的输入b0~b7由7bit数据和1bit校验位组成。Fod为判奇输出,Fev为判偶输出。当采用奇校验时,Fod = 1,Fev = 0;当采用偶校验时,Fod = 0,Fev = 1。
例如,采用奇校验检测“1100111”,数据包含5个“1”,校验位为“0”,校验器的输入b0~b7为“11001110”,Fod = 1, Fev = 0。
采用结构描述方式的电路代码如下:
module checker1 (Fod, Fev, b);
output Fod, Fov;
input [7:0] b;
wire w1, w2, w3, w4, w5, w6;
xor U1(w1, b[0], b[1]);
xor U2(w2, b[2], b[3]);
xor U3(w3, b[4], b[5]);
xor U4(w4, b[4], b[5]);
xor U5(w5, w1, w2);
xor U6(w6, w3, w4);
xor U7(Fod, w5, w6);
not U8(Fov, Fod);
endmodule
采用抽象描述方式的电路代码如下:
module checker2 (Fod, Fov, b);
output Fod, Fov;
input[7:0] b;
assign Fod = ^b;//按位异或
assign Fev = ~Fod;
endmodule