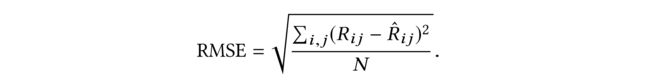2019_KDD_Social Recommendation with Optimal Limited Attention
[论文阅读笔记]2019_KDD_Social Recommendation with Optimal Limited Attention
论文下载地址: https://doi.org/10.1145/3292500.3330939
发表期刊:KDD
Publish time: 2019
作者及单位:
- Xin Wang [email protected] Tsinghua University
- Wenwu Zhu∗ [email protected] Tsinghua University
- Chenghao Liu∗ [email protected] Singapore Management University
数据集: 正文中的介绍
- Douban http://movie.douban.com/
- https://www.cse.cuhk.edu.hk/irwin.king.new/pub/data/douban
- CiaoDVD http://dvd.ciao.co.uk
- Epinions http://www.trustlet.org/wiki/Epinions_dataset
- http://www.epinions.com/
- Flixster http://www.cs.ubc.ca/~jamalim/datasets/
- http://www.flixster.com/
代码:
- (文中没给)
其他:
其他人写的文章
简要概括创新点:
- (1) Limited attention is very important to social recommendation as it has been proved to have significant impact on users’ online behaviours. (有限的关注对社交推荐非常重要,因为事实证明它对用户的在线行为有重大影响。)
- (2)Therefore, we propose to incorporate limited attention, a well-studied social science notion into social recommendation in an appropriate way. (因此,我们建议以适当的方式将有限的注意力、经过充分研究的社会科学概念纳入社会推荐中。)
- We first formulate the optimal limited attention problem, aiming to optimally bring the concept of limited attention into social recommendation. (我们首先提出了最优有限注意问题,旨在将有限注意的概念最优地引入到社会推荐中。)
- Then we develop a novel model which efficiently finds an optimal number of friends whose preferences have the best impact on the target user and adaptively learns an optimal personalized attention towards every selected friend, as well as the latent preference for each user. (然后,我们开发了一个新的模型,该模型可以有效地找到对目标用户的偏好影响最大的最佳朋友数,并自适应地学习对每个选定朋友的最佳个性化注意,以及每个用户的潜在偏好。)
- (3)we detailedly explain our proposed OLA-Rec model which incorporates the concept of optimal limited attention into social recommendation. (我们详细解释了我们提出的LA-Rec模型,该模型将最优有限注意的概念融入到社会推荐中。)
- (4)we incorporate the concept of optimal limited attention into social recommendation through combining the optimal k ∗ k^∗ k∗ and α ∗ \alpha^∗ α∗ with matrix factorization. Generally, we estimate user i i i’s rating on item j j j, R i j R_{ij} Rij, through the dot product of social factor ϕ i \phi_i ϕi and item j j j’s latent feature vector V j V_j Vj: (接下来,我们将最优有限注意的概念结合到社会推荐中,通过在矩阵分解中结合 k ∗ k^∗ k∗ and α ∗ \alpha^∗ α∗ )
- (5)We then develop a novel algorithm through employing an EM-style strategy to jointly optimize users’ latent preferences, optimal number of their best influential friends and the corresponding attentions. (然后,我们开发了一种新的算法,通过使用EM风格的策略来联合优化用户的潜在偏好、他们最有影响力的朋友的最佳数量以及相应的注意事项。)
- (6) 细节
- we define users rating less than five items as cold-start users. Figure 5 depicts the performances of various methods on cold start users. (我们将评分低于五项的用户定义为冷启动用户)
- We remove users with less than 2 ratings and select 80% of each user’s ratings at random for training, leaving the remainder as test set. (我们删除评分低于2的用户,并随机选择每个用户评分的80%进行训练,剩下的作为测试集。)
ABSTRACT
- (1) Social recommendation has been playing an important role in suggesting items to users through utilizing information from social connections. However, most existing approaches do not consider the attention factor causing the constraint that people can only accept a limited amount of information due to the limited strength of mind, which has been discovered as an intrinsic physiological property of human by social science. (社会推荐在利用社会关系信息向用户推荐商品方面发挥着重要作用。然而,大多数现有的方法没有考虑到注意力因素导致的约束,人们只能接受有限数量的信息,由于有限的精神力量,这已被发现作为人类社会科学的内在生理属性。)
- We address this issue by resorting to the concept of limited attention in social science and combining it with machine learning techniques in an elegant way. (我们通过诉诸社会科学中有限关注的概念并以优雅的方式将其与机器学习技术相结合来解决这个问题。)
- When introducing the idea of limited attention into social recommendation, two challenges that fail to be solved by existing methods appear: (将有限关注引入社会推荐时,出现了两个现有方法无法解决的挑战:)
- (i) how to develop a mathematical model which can optimally choose a subset of friends for each user such that these friends’ preferences can best influence the target user, and (如何建立一个数学模型,为每个用户最佳地选择朋友子集,使这些朋友的偏好能够最好地影响目标用户,以及)
- (ii) how can the model learn an optimal attention for each of these selected friends. (模型如何为每个选定的朋友学习最佳注意力。)
- To tackle these challenges, we first propose to formulate the problem of optimal limited attention in social recommendation. (为了应对这些挑战,我们首先提出了社会推荐中的最优有限关注问题。)
- We then develop a novel algorithm through employing an EM-style strategy to jointly optimize users’ latent preferences, optimal number of their best influential friends and the corresponding attentions. (然后,我们开发了一种新的算法,通过使用EM风格的策略来联合优化用户的潜在偏好、他们最有影响力的朋友的最佳数量以及相应的注意事项。)
- We also give a rigorous proof to guarantee the algorithm’s optimality. (我们也给出了严格的证明来保证算法的最优性。)
- The proposed model is capable of efficiently finding an optimal number of friends whose preferences have the best impact on target user as well as adaptively learning an optimal personalized attention towards every selected friend w.r.t. the best recommendation accuracy. (该模型能够有效地找到对目标用户影响最大的最佳好友数,并能自适应地学习对每个选定好友的最佳个性化注意,从而获得最佳推荐准确率。)
- Extensive experiments on real-world datasets demonstrate the superiority of our proposed model over several state-of-the-art algorithms. (在真实数据集上的大量实验表明,我们提出的模型优于几种最先进的算法。)
CCS CONCEPTS
• Information systems → Social recommendation.
KEYWORDS
Recommendation, User Behavior Modeling, Limited Attention
1 INTRODUCTION
-
(1) Being capable of efficiently filtering the exploding information on Internet, recommender systems have become an indispensable tool in recommending relevant items that may potentially be attractive to users. As a hot research topic, recommendation with no doubt has received a lot of attention from both academy and industry [1, 28]. Nevertheless, traditional recommender systems suffer from data sparsity which is caused by the fact that the number of items is normally very huge while users commonly consume only a very small portion of these items. In addition, traditional recommendation approaches have a deteriorative performance on new users without any historical behaviours, resulting in the cold start problem. This brings the idea of social recommendation which utilizes social information from social connections (such as friends) to mitigate the above two problems [11, 19]. (由于能够有效过滤互联网上爆炸式增长的信息,推荐系统已经成为推荐可能吸引用户的相关项目的不可或缺的工具。作为一个热门研究课题,推荐无疑受到了学术界和业界的广泛关注[1,28]。然而,传统的推荐系统存在数据稀疏的问题,这是由于项目的数量通常非常庞大,而用户通常只消费其中的一小部分。 此外,传统的推荐方法在没有任何历史行为的新用户身上表现不佳,导致冷启动问题。这就产生了社会推荐的概念,它利用来自社会关系(如朋友)的社会信息来缓解上述两个问题[11,19]。)
-
(2) Although there have been a lot of works on social recommendation, most of them ignore the attention factor which results in the constraint that only a small portion of information can be processed in real time by each individual due to her limited mind strength and brain capacity [13, 27]. (虽然有很多关于社会推荐的研究,但大多数都忽略了注意力因素,这导致了由于每个人的脑力和大脑容量有限,只能实时处理一小部分信息的限制[13,27]。)
- Recent works [4, 8, 10, 37] have also confirmed the important role this factor plays in affecting people’s behaviours and their interactions in social media. Actually people now with online social networks are easier to get connected, especially for those who are not close enough to become friends off-line, causing the fact that many of our friends on social networks may produce noisy/useless information. This being the case, bringing the concept of attention factor into social recommendation becomes very necessary. (最近的研究[4,8,10,37]也证实了这个因素在影响人们在社交媒体上的行为和互动中所起的重要作用。事实上,现在拥有在线社交网络的人更容易获得联系,尤其是那些关系不够亲密而无法成为离线朋友的人,这导致我们在社交网络上的许多朋友可能会产生嘈杂/无用的信息。在这种情况下,将注意力因素的概念引入到社会推荐中变得非常必要。)
- The only two works [14, 15] considering the attention factor in recommendation simply assign non-zero weights to all social connections. (考虑到推荐中的注意因素,仅有两个工作[14,15]只是将非零权重分配给所有社会关系。)
- On the one hand, this fails to simulate the real-world scenario where people only take information from a small number of friends into consideration and ignore useless information produced by all other friends who have noisy influence on the target user. (一方面,这无法模拟现实世界中人们只考虑少数朋友的信息,而忽略对目标用户有噪音影响的所有其他朋友产生的无用信息。)
- On the other hand, aggregation of preferences from all social connections is computationally expensive and timeconsuming when making recommendation to users (especially for those who have a huge number of connections). (另一方面,当向用户(尤其是那些拥有大量社交网络的用户)推荐时,聚合所有社交网络的偏好在计算上既昂贵又耗时。)
- Overall, none of existing works in social recommendation could handle the problem related to attention factor appropriately or efficiently. (总的来说,现有的社会推荐工作都不能恰当或有效地处理与注意因素相关的问题。)
-
(3) To address the above problem in social recommendation, we borrow the idea of limited attention, a well-documented psychological and cognitive concept from social science that can affect user behaviours. (为了解决社会推荐中的上述问题,我们借用了有限关注的概念,这是一个来自社会科学的心理学和认知概念,可以影响用户行为。)
- The insights from social science and computer science inspire us to incorporate the notion of limited attention into social recommendation in a more appropriate and efficient way, considering that people may only take information from a limited number of their social connections into account. (来自社会科学和计算机科学的见解启发我们以更恰当、更有效的方式将有限注意力的概念纳入社会推荐中,因为人们可能只考虑有限数量的社会关系中的信息。)
- That is to say, each individual should be influenced by only a limited number of her social connections and thus her preference should also depend only on the preferences of these social connections. (也就是说,每个人应该只受有限的社会关系的影响, 因此她的偏好也应该只取决于这些社会关系的偏好。)
- Besides, it is shown that social connections normally receive non-uniform distributed attentions from the target user and thus have different influence on her [7]. (此外,研究还表明,社交关系通常从目标用户那里获得非均匀分布的注意力,因此对目标用户有不同的影响[7]。)
-
(4) Therefore, two challenges exist:
- (i) How can we develop an algorithm capable of filtering out an optimal group of friends for each user such that these friends’ preferences can best influence the target user and (我们如何开发一种算法,能够为每个用户筛选出一组最佳的朋友,以便这些朋友的偏好能够最好地影响目标用户和用户)
- (ii) How to learn an optimal personalized attention towards each of these selected friends for every target user. (如何为每个目标用户学习对每个选定朋友的最佳个性化关注。)
- Obviously none of previous works are able to resolve the first challenge. (显然,以前的工作都无法解决第一个挑战)
- One naive way of implementing such subset selection on the set of friends may be to find the distance between users and their friends, then fill up the set of useful friends by adding friends sequentially in order beginning from the closest one first, imposing a threshold at a level where, say, the distance is equivalent to the distance to people that are not explicit friends. (在朋友集上实现这种子集选择的一种简单方法可能是找到用户和他们的朋友之间的距离,然后通过从最接近的朋友开始按顺序添加朋友来填充有用的朋友集,将阈值设置为,这种距离相当于与非明确朋友之间的距离。)
- This seems to be quite straightforward and intuitive, but how to calculate the distance between users may have a significant influence on the selection outcome and there are too many of them (PCC, Cosine, etc.) that we can choose. (这似乎非常简单直观,但如何计算用户之间的距离可能会对选择结果产生重大影响,我们可以选择的太多(PCC、余弦等)。)
- More importantly, some commonly adopted distance calculation metric such as PCC even fails to optimally capture the similarities between two users (discussed in Section 3.2). (更重要的是,一些常用的距离计算指标,如PCC,甚至无法最佳地捕捉两个用户之间的相似性(在第3.2节中讨论)。)
- As for the second challenge, existing work [20] calculates the weight for each friend through the Pearson Correlation Coefficient (PCC) between her and the target user, which is suboptimal because PCC is static and independent of user latent feature vectors (more details will be discussed in Section 3.2). (至于第二个挑战,现有工作[20]通过他和目标用户之间的皮尔逊相关系数(PCC)计算每个朋友的权重,这是次优的,因为PCC是静态的,独立于用户潜在特征向量(更多细节将在第3.2节中讨论)。)
-
(5) To handle these two challenges, we elegantly combine social science concepts with machine learning techniques and formulate the problem of optimal limited attention in the context of social recommendation. (为了应对这两个挑战,我们巧妙地将社会科学概念与机器学习技术相结合,并在社会推荐的背景下提出了最佳有限注意力问题。)
-
We then propose a novel social recommendation model capable of (然后,我们提出了一种新的社会推荐模型,该模型能够)
- (i) selecting an optimal number of social connections for each individual efficiently such that the preferences of these chosen friends are able to best influence the target user, and (有效地为每个人选择社交关系的最佳数量,以便这些选定朋友的偏好能够对目标用户产生最佳影响,以及)
- (ii) learning the optimal attentions from the target user towards these chosen friends adaptively as well. (学习目标用户对这些选定朋友的最佳注意力)
-
To be more concrete,
- we first employ latent feature factors obtained through matrix factorization to express the latent user and item preferences. (我们首先使用通过矩阵分解获得的潜在特征因子来表达潜在用户和项目偏好。)
- Then we develop a novel algorithm to simultaneously learn the optimal number of influential social connections, their corresponding optimal attentions from each target individual and other model parameters including the latent feature vector for each user and each item. The proposed algorithm has an advantage in a joint optimization of finding the ‘optimal’ combination of influential social connections and the corresponding attentions as well as other parameters rather than a two-stage procedure. (然后,我们开发了一种新的算法来同时学习每个目标个体中有影响力的社会关系的最佳数量、它们对应的最佳注意以及其他模型参数,包括每个用户和每个项目的潜在特征向量。该算法在联合优化中的优势在于找到有影响力的社会关系和相应注意事项以及其他参数的“最佳”组合,而不是两阶段过程。)
-
Experiments on real-world datasets demonstrate the improvement of our proposed model against state-of-the-art approaches. (在真实数据集上的实验表明,我们提出的模型相对于最先进的方法有所改进。)
-
(6) To recapitulate, the highlight of this paper is that inspired by the sociological discoveries, we develop a model which combines social science concepts and mathematical formulations in an elegant way. We address the challenges raised in social science by means of machine learning techniques in the context of social recommendation. We believe our elegant combination of machine learning with social science can help to achieve a performance boost in terms of social recommendation accuracy. (综上所述,本文的重点是受社会学发现的启发,我们开发了一个模型,以优雅的方式将社会科学概念和数学公式结合起来。我们在社会推荐的背景下,通过机器学习技术解决社会科学中提出的挑战。我们相信,我们将机器学习与社会科学完美结合,有助于提高社会推荐的准确性。)
-
The contributions of this paper are summarized as follows. (本文的贡献总结如下。)
- Motivated by the challenges discovered in social science, we propose to combine machine learning techniques with social science concepts, and formulate the problem ofoptimal limited attention in social recommendation. (基于在社会科学中发现的挑战,我们提出将机器学习技术与社会科学概念相结合,并提出在社会推荐中最佳有限关注的问题。)
- We develop a novel algorithm that is able to pick up a group of social connections (friends) for each individual efficiently such that the preferences of these chosen friends can best influence the target user, and then learn the optimal attentions from the target user towards these chosen friends adaptively with respect to the best recommendation accuracy. (我们开发了一种新的算法,能够有效地为每个人挑选一组社会关系(朋友),以便这些选择的朋友的偏好能够最好地影响目标用户,然后根据最佳推荐准确率自适应地学习目标用户对所选朋友的最佳关注。)
- We show the optimality of our proposed model in selecting the optimal number of social connections as well as adaptively learning the attentions. (我们证明了我们提出的模型在选择最佳的社会关系数以及自适应地学习注意方面的最优性。)
- We conduct extensive experiments on real-world datasets to show that our proposed algorithm can clearly beat existing approaches in various evaluation metrics. (我们在真实数据集上进行了大量实验,结果表明,我们提出的算法可以在各种评估指标上明显优于现有的方法。)
2 RELATED WORK
2.1 Collaborative Filtering.
- (1) Being capable of predicting user preferences through uncovering complex and unexpected patterns hidden in users’ past behaviours without any domain knowledge, collaborative filtering has become one of the most popular methods in recommender systems. (由于能够在没有任何领域知识的情况下,通过发现隐藏在用户过去行为中的复杂和意外模式来预测用户偏好,协同过滤已成为推荐系统中最流行的方法之一。)
- Collaborative filtering methods generally can be classified into memory-based methods and model-based methods [31]. (协同过滤方法通常可分为基于记忆的方法和基于模型的方法[31])
- Memory-based approach can be further categorized as user-based and item-based approaches, according to which of similar users and similar items will be taken into account. (基于记忆的方法可以进一步分为基于用户的方法和基于项目的方法,根据这两种方法,相似的用户和相似的项目将被考虑。)
- User- based methods predict an unknown rating from a target user on a target item through calculating the weighted average of all the ratings on the target item from users similar to the target user, (基于用户的方法通过计算与目标用户相似的用户对目标项目的所有评分的加权平均值,预测目标用户对目标项目的未知评分,)
- while item-based methods obtain the rating from a target user on a target item via computing the average ratings by the same user on items similar to the target item. (基于项目的方法通过计算同一用户对与目标项目相似的项目的平均评分来获得目标用户对目标项目的评分。)
- In contrast to the memory-based methods, model-based approaches operate the observed ratings scores with the help of machine learning techniques to train a predefined learning model which will later be used to predict unknown ratings. (与基于记忆的方法相比,基于模型的方法借助机器学习技术对观察到的评分进行操作,以训练预定义的学习模型,该模型稍后将用于预测未知评分。)
- Matrix factorization, as one of the most widely used model-based collaborative filtering methods, has achieved a promising success in both academia and industry [16, 33]. Among the literature of matrix factorization, Salakhutdinov and Mnih [23] propose a probabilistic version of matrix factorization whose time complexity is linear in the number of observations and is more resistant the overfitting problem. We refer readers to a general treatment [17] for detailed introduction on matrix factorization in recommendation. (矩阵分解作为最广泛使用的基于模型的协同过滤方法之一,在学术界和工业界都取得了巨大的成功[16,33]。在矩阵分解的文献中,Salakhutdinov和Mnih[23]提出了一种概率形式的矩阵分解,其时间复杂度在观测值的数量上是线性的,并且更能抵抗过拟合问题。我们建议读者参考一般处理方法[17],详细介绍建议中的矩阵分解。)
- Recent works on collaborative filtering [23, 26, 29, 30] take notice of the fact that only a small number of factors are important (sparseness) and one user’s preference vector is determined by how each factor applies to that user. Therefore, these methods focus on factorizing the user-item rating matrix with low-rank representations which will then be utilized to make further predictions. (最近关于协同过滤的研究[23,26,29,30]注意到,只有少数因素是重要的(稀疏性),一个用户的偏好向量取决于每个因素如何应用于该用户。因此,这些方法侧重于用低秩表示分解用户项目评分矩阵,然后利用这些矩阵进行进一步预测。)
2.2 Social Recommendation.
- (1) Since users become connected through online social networks, their preferences are no longer independently and identically distributed. Therefore, correlated relationships among connected users that provide social information have drawn more and more interests from researchers [36]. (由于用户通过在线社交网络连接起来,他们的偏好不再是独立同分布的。 因此,提供社会信息的互联用户之间的相关关系吸引了越来越多研究人员的兴趣[36]。)
- For instance, Weng et al. [38] find that users with social connections are more likely to share similar interests in various topics than two randomly chosen users, and Tang et al. [32] show that users with trust relations are more likely to have similar preferences in item ratings. (例如,翁等人[38]发现,与随机选择的两个用户相比,有社交关系的用户更有可能在各种主题上分享相似的兴趣,而唐等人[32]则表明,有信任关系的用户更有可能在项目评分上有相似的偏好。)
- These phenomena can be observed in most online social networks and explained by social influence [21] as well as homophily [22] in social correlation theories. (这些现象可以在大多数在线社交网络中观察到,并可以用社会影响[21]以及社会关联理论中的同质性[22]来解释。)
- This motivates the advent of social recommendation [3, 5, 9, 12, 18, 20, 24, 25, 39–45] . (这促使了社会推荐的出现)
- Particularly, Ma et al. [19] propose a probabilistic matrix factorization model through factorizing user-item rating matrix and user-user linkage matrix simultaneously. (特别是,Ma等人[19]通过同时分解用户项目评分矩阵和用户链接矩阵,提出了一种概率矩阵分解模型。)
- Later another matrix factorization model aggregating a user’s own rating and her friends’ ratings to predict the target user’s final rating on an item is introduced by them as well [18]. (后来,他们还引入了另一个矩阵分解模型,将用户自己的评分和她朋友的评分聚合起来,以预测目标用户对某个项目的最终评分[18]。)
- Jamali and Ester [12] formulate another matrix factorization model based on the assumption that users’ latent feature vectors are dependent on their social ties’. (Jamali和Ester[12]在假设用户的潜在特征向量依赖于他们的社会关系的基础上,提出了另一个矩阵分解模型。)
- There also exist several works trying to incorporate the concept of strong and weak ties into social recommendation. (也有一些作品试图将强关系和弱关系的概念融入社会推荐中)
- Wang et al. [35] integrate the concepts of strong and weak ties documented in social science into social recommendation through presenting a more fine-grained categorization of user-item feedback for Bayesian Personalized Ranking by leveraging the knowledge of tie strength and tie types. They later enable the learning of personalized tie type preference for each individual in probabilistic matrix factorization [34]. (Wang等人[35]通过利用领带强度和领带类型的知识,对用户项目反馈进行更细粒度的分类,为贝叶斯个性化排名,将社会科学中记录的强领带和弱领带的概念整合到社会推荐中。之后,它们可以在概率矩阵分解中学习每个个体的个性化领带类型偏好[34]。)
2.3 Limited Attention.
- (1) Limited attention is a concept widely discussed in social science [13, 27] and Kang et al. [14, 15] are the first to consider it in recommendation.
- However, they simply assign non-zero attentions (weights) to all social connections (friends), failing to simulate the real-world scenario where people with limited attention only take information from a small number of friends into consideration and ignore useless information produced by all other friends who have noisy influence on the target user. (然而,他们只是将非零关注(权重)分配给所有社会关系(朋友),未能模拟现实世界中注意力有限的人只考虑少数朋友的信息,而忽略所有其他对目标用户有噪音影响的朋友产生的无用信息。)
- Moreover, aggregation of preferences from all social connections is computationally expensive and time-consuming when making recommendation to users (especially those who have a huge number of social connections). Our proposed optimal limited attention social recommendation model in this paper overcomes previous works’ disadvantages through finding an optimal subset of best influential friends for each individual and calculating the optimal corresponding attentions for these selected friends. (此外,当向用户(尤其是那些拥有大量社交网络的用户)推荐时,将所有社交网络的偏好聚合在一起,在计算上既昂贵又耗时。本文提出的最优有限注意社会推荐模型克服了以往研究的不足,通过为每个个体寻找最佳有影响力的朋友子集,并计算这些朋友的最佳对应注意。)
3 SOCIAL RECOMMENDATION WITH OPTIMAL LIMITED ATTENTION
- (1) In this section, we first give a problem definition on the application of matrix factorization in recommendation as prior knowledge. We then define the problem of optimal limited attention in which limited attention is elegantly brought to social recommendation.
- (2) Finally, we detailedly explain our proposed OLA-Rec model which incorporates the concept of optimal limited attention into social recommendation. (在这一部分中,我们首先给出一个关于矩阵分解作为先验知识在推荐中应用的问题定义。然后我们定义了最优有限注意问题,其中有限注意被优雅地引入到社会推荐中。最后,我们详细解释了我们提出的LA-Rec模型,该模型将最优有限注意的概念融入到社会推荐中。)
3.1 Problem Definition
-
(1) In recommender systems, we are given a set of users U U U and a set of items I I I,
- as well as a ∣ U ∣ × ∣ I ∣ |U| × |I| ∣U∣×∣I∣ rating matrix R R R whose non-empty (observed) entries R i j R_{ij} Rij represent the feedbacks (e.g., ratings, clicks etc.) of user i ∈ U i \in U i∈U for item j ∈ I j \in I j∈I.
- When it comes to social recommendation, another ∣ U ∣ × ∣ U ∣ |U| × |U| ∣U∣×∣U∣ social tie matrix T T T whose non-empty entries T i u T_{iu} Tiu denote i ∈ U i \in U i∈U and u ∈ U u \in U u∈U are ties, may also be necessary.
- The task is to predict the missing values in R R R, i.e., given a user u ∈ U u \in U u∈U and an item p ∈ I p \in I p∈I for which R u p R_{up} Rup is unknown, we predict the rating of u u u for p p p using observed values in R R R and T T T (if available).
-
(2) A matrix factorization model assumes the rating matrix R R R can be approximated by a multiplication of d d d-rank factors,

- where U ∈ R d × ∣ U ∣ U \in R^{d\times |U|} U∈Rd×∣U∣ and V ∈ R d × ∣ I ∣ V \in R^{d\times |I|} V∈Rd×∣I∣.
- Normally d d d is far less than both ∣ U ∣ |U| ∣U∣ and ∣ I ∣ |I| ∣I∣.
- Thus given a user i i i and an item j j j, the rating R i j R_{ij} Rij of i i i for j j j can be approximated by the dot product of user latent feature vector U i U_i Ui and item latent feature V j V_j Vj,
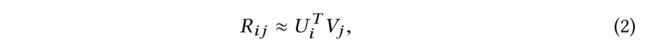
- where U i ∈ R d × 1 U_i \in R^{d×1} Ui∈Rd×1 is the i t h i_{th} ith column of U U U and V j ∈ R d × 1 V_j \in R^{d\times 1} Vj∈Rd×1 is the j t h j_th jth column of V V V.
- For ease of notation, we let ∣ U ∣ = M |U| = M ∣U∣=M and ∣ I ∣ = N |I| = N ∣I∣=N in the remaining of the paper.
3.2 Considering Optimal Limited Attention
- We define the optimal limited attention problem in Problem 1. (我们在问题1中定义了最优有限注意力问题。)
Problem 1. Optimal Limited Attention (OLA)
-
(1) Given a set of users, their social linkage information, a set of items as well as a subset of user-item ratings as input in the context of social recommendation, for each user select an optimal subset of her friends such that these friends’ preferences can best influence this user and learn an optimal attention for each of these selected friends. (给定一组用户、他们的社交链接信息、一组项目以及用户项目评分子集,作为社交推荐的输入,对于每个用户,选择其朋友的最佳子集,以便这些朋友的偏好能够最好地影响该用户,并为每个选定的朋友学习最佳关注度。)
-
(2) Existing social recommendation models either simply treat different social connections equally or employ Pearson Correlation Coefficient (PCC) to calculate similarities between users. (现有的社会推荐模型要么简单地平等对待不同的社会关系,要么采用皮尔逊相关系数(PCC)计算用户之间的相似性。)
- On the one hand, giving each social connection equal attention is not optimal because of the non-uniform distributions among friendships [7]. (一方面,由于友谊之间的分布不均匀,给予每个社会关系同等的关注并不是最优的[7]。)
- On the other hand, the calculation of PPC between two users i i i and f f f is based on those common items that these two users both rate, as is shown in (3). (另一方面,两个用户 i i i和 f f f之间的PPC计算是基于这两个用户都对其进行评分的公共项目,如(3)所示。)

- where I ( ⋅ ) I(\cdot) I(⋅) denotes the set of items rated by the corresponding user and (表示由相应用户评定的项目集)
- R ˉ \bar{R} Rˉ denotes the average rating score of the corresponding user. ( R ˉ \bar{R} Rˉ表示对应用户的平均评分。)
- We give an instance in which PCC fails to optimally capture the similarities between two users as follows. Suppose user i i i and u u u have exactly the same latent feature vector (0, 0, 0, 0.9, 0.1, 0, 3), and item j j j and k k k also have the same latent feature vector (0, 0, 0, 0.5, 4, 0, 0.2). (我们给出了一个例子,其中PCC未能最佳地捕获两个用户之间的相似性,如下所示。假设用户 i i i和 u u u具有完全相同的潜在特征向量(0,0,0,0.9,0.1,0,3),项目 j j j和 k k k也具有相同的潜在特征向量(0,0,0,0,0.5,4,0,0.2)。)
- Let us consider the scenario where i i i only rates j j j and u u u only rates k k k. The PCC similarity between user i i i and u u u is apparently 0, which is reasonable according to the definition of PCC but obviously not realistic. (让我们考虑的情况下, i i i只对 j j j评分和 u u u只对 k k k评分。PCC相似性之间的用户 i i i和 u u u显然是0,这是合理的,根据PCC的定义,但显然不现实。)
-
(3) Furthermore, we can also observe from (3) that PCC is static and independent of user latent feature vectors. Therefore, applying PCC similarity to the calculation of attentions between users will result in a suboptimal result. (此外,我们还可以从(3)中观察到,PCC是静态的,与用户潜在的特征向量无关。 因此,将PCC相似度应用于用户之间关注度的计算将导致次优结果。)
-
(3) As a conclusion, all the existing approaches fail to solve the optimal limited attention problem. (综上所述,现有的方法都无法解决最优有限注意问题。)
3.3 OLA-Rec: Social Recommendation with Optimal Limited Attention
-
(1) To solve Problem 1, we propose a novel algorithm OLA-Rec which is capable of finding an optimal number of best influential friends and their corresponding attentions from each target user. (为了解决问题1,我们提出了一种新的算法OLA Rec,该算法能够从每个目标用户中找到最佳数量的最有影响力的朋友及其相应的注意事项。)
-
(2) We begin by introducing a new d × 1 d \times 1 d×1 vector ϕ i \phi_i ϕi for each user i i i, such that
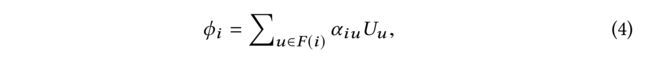
- where F ( i ) F(i) F(i) is the set of user i i i’s friends and α i u α_{iu} αiu is the attention from i i i to u u u.
- We further constrain α i u ≥ 0 α_{iu} \ge 0 αiu≥0 and ∑ u = 1 ∣ F ( i ) ∣ \sum^{|F(i)|}_{u=1} ∑u=1∣F(i)∣ so that all variables are in a comparable magnitude.
- We denote ϕ i \phi_i ϕi as the social factor which is an aggregation of the influence of user i i i’s friends, weighted by attentions ( α i ⋅ ) (α_{i·}) (αi⋅) from i i i.
- Larger α i u \alpha_{iu} αiu indicates user u u u receives more attention from user i i i and has more impact on i i i.
- Similarly, smaller α i u \alpha_{iu} αiu means user u u u receives less attention from user i i i and is less important in influencing i i i.
-
We minimize the absolute difference between ϕ i \phi_i ϕi and α i u U u \alpha_{iu}U_u αiuUu so that they are close to each other:

-
(2) As we discussed, the challenge in Problem 1 is to find an optimal number of best influential friends for each individual and learn the optimal attention for them with respect to the best recommendation accuracy. We start to tackle this challenge by considering the following inequality based on (5): (正如我们所讨论的,问题1中的挑战是为每个人找到最佳数量的最有影响力的朋友,并了解他们在最佳推荐准确性方面的最佳关注度。我们开始通过考虑以下基于(5)的不平等来应对这一挑战:)

- where L L L is the Lipschitz constant of ϕ i \phi_i ϕi given its Lipschitz continuity and ( L L L是 ϕ i \phi_i ϕi的Lipschitz常数,考虑到其Lipschitz连续性)
- d ( ⋅ , ⋅ ) d(·, ·) d(⋅,⋅) is a preset distance function (Euclidean distance in this paper). (是一个预设的距离函数(本文中的欧几里德距离)。)
- By Hoeffding’s inequality, with probability at least 1 − δ 1 − \delta 1−δ, we have : (根据霍夫丁不等式,至少有概率 1 − δ 1 − \delta 1−δ)
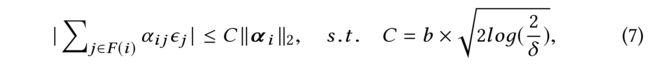
- whose proof will be given in Appendix B.
- Here we assume that ∣ ϵ j ∣ ≤ b |\epsilon_j| \le b ∣ϵj∣≤b for some given b > 0 b > 0 b>0 to bound ϵ \epsilon ϵ.
- In addition, it is also assumed that { ϵ i } i = 1 n \{\epsilon_i\}^n_{i=1} {ϵi}i=1nare independent so that we are able to apply Hoeffding’s inequality and bound the so-called variance. (是独立的,所以我们可以应用霍夫丁不等式,并限制所谓的方差。)
-
(3) The assumption of Lipschitz continuous function, on the other hand, is required to bound the so-called bias term. Thus there comes another optimization problem from (6) such that solving it could obtain a guarantee for (5) with high probability: (另一方面,Lipschitz连续函数的假设需要约束所谓的偏差项。因此,从(6)中得到了另一个优化问题,解决它可以以高概率获得(5)的保证:)

-
(4) and user i i i’s friends u ∈ F ( i ) u \in F(i) u∈F(i) are assumed to be in an ascending order with respect to d ( U u , U i ) d(U_u, U_i) d(Uu,Ui). (假设是按升序排列的)
- In fact, we only need to set the value of L C L_C LC ratio which equals to L / C L/C L/C in (9) rather than setting ϵ \epsilon ϵ and b b b during practical implementation. (实际上,我们只需要设置 L C L_C LC的值比等于(9)中的 L / C L/C L/C,而不是在实际实施过程中设置 ϵ \epsilon ϵ和 b b b。)
- We will discuss the impact of L C L_C LC ratio later in the experimental section. L C L_C LC ratio indirectly determines the attention weights α \alpha α and the value of optimal k ∗ k^∗ k∗ which will in turn influence the selected subsets of social connections. (我们将讨论 L C L_C LC的影响比率 稍后在实验部分。 L C L_C LC比率间接决定了注意力权重 α \alpha α和最佳 k ∗ k^∗ k∗这反过来会影响社会关系的选定子集。)
- Therefore, we test different settings of L C L_C LC ratio and examine the corresponding effects on the performances in later experiments. (因此,我们测试了 L C L_C LC的不同设置,并在以后的实验中检查相应的性能影响。)
-
(5) Inspired by Anava’s work [2], we come out with the following theorem and corollary: (受Anava’s工作[2]的启发,我们得出了以下定理和推论:)
Theorem 3.1.
- (1) The optimal α i \alpha_i αi of (8) for each user i i i, denoted as α i ∗ \alpha^∗_i αi∗, can be written in the following form:

- where we require β i u < λ \beta_{iu} < \lambda βiu<λ for some λ > 0 \lambda > 0 λ>0 in (10).
Proof.
-
(1) Consider the alternative expression in (8), i.e., m i n α i C ( ∥ α i ∥ 2 + α i T β ) min_{\alpha_i} C( ∥\alpha_i∥_2+ \alpha^T_i β) minαiC(∥αi∥2+αiTβ), by ignoring C and introducing the Lagrange Multipliers, we have: (通过忽略 C C C并引入拉格朗日乘数,我们得到:)
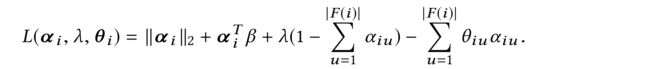
-
(2) Given the convexity of (8), a global optimum is guaranteed for any solution satisfying the KKT conditions. Take the partial derivative of Lagrangian with respect to α i \alpha_i αi, set it to 0: (给定(8)的凸性,对于满足KKT条件的任何解,都保证全局最优。取拉格朗日对 α i \alpha_i αi的偏导数,设为0:)
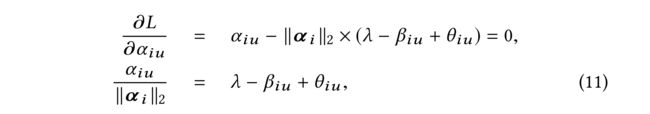
- where ∀ α i u > 0 \forall \alpha_{iu} > 0 ∀αiu>0, θ i u = 0 \theta_{iu} = 0 θiu=0 (i.e., β i u < λ \beta_{iu} < λ βiu<λ) and
- ∀ a l p h a i u = 0 \forall alpha_{iu} = 0 ∀alphaiu=0, θ i u ≥ 0 \theta_{iu} \ge 0 θiu≥0 (i.e., β i u ≥ λ \beta_{iu} \ge \lambda βiu≥λ) by KKT conditions.
-
(3) Thus for any optimal attention α i u ∗ > 0 α^∗_{iu} > 0 αiu∗>0, we have:
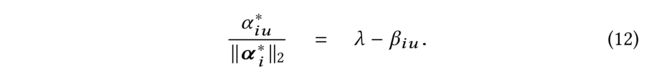
-
(4) Further combining (12) with the constraint that ∑ u = 1 ∣ F ( i ) ∣ α i u = 1 \sum^{|F(i)|}_{u=1} \alpha_{iu} = 1 ∑u=1∣F(i)∣αiu=1, any α i u ∗ > 0 α^∗_{iu} > 0 αiu∗>0 can be calculated as follows:
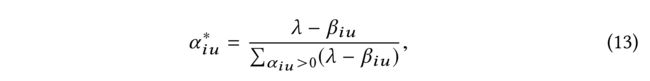
- which completes the proof.
-
A direct statement from Theorem 3.1 is as follows.
Corollary 3.2.
*There exists 1 ≤ k i ∗ ≤ ∣ F ( i ) ∣ 1 ≤ k^∗_i≤ |F(i)| 1≤ki∗≤∣F(i)∣ whose relation to α i ∗ α^∗_i αi∗ in Theorem 3.1 is as follows: ∀ u > k i ∗ \forall u > k^∗_i ∀u>ki∗, α i u ∗ = 0 α^∗_{iu} = 0 αiu∗=0 and ∀ u ≤ k i ∗ ∀u \le k^∗_i ∀u≤ki∗, α i u ∗ > 0 α^∗_{iu} > 0 αiu∗>0.
-
(5) Theorem 3.1 and Corollary 3.2 confirm the existence of optimal solution for Problem 1, which is that for each target user i i i, k i ∗ k^∗_i ki∗ is the optimal number of best influential friends needed whose attentions from i should be non-zero and whose attentions correspond to the k i ∗ k^∗_i ki∗ smallest values of β i β_i βi. (定理3.1和推论3.2证实了问题1的最优解的存在性,即每个目标用户 i i i的最优解。 k i ∗ k^*_i ki∗是所需的最佳有影响力的朋友数量,这些朋友的关注度应为非零,并且其关注度应与 β i β_i βi的 k i ∗ k^∗_i ki∗个最小值对应 )
- We will show how the optimal solution α i ∗ \alpha^∗_i αi∗ can be efficiently found and be incorporated in social recommendation. The following equation can be obtained by squaring and summing both sides in (12) over all non-zero α i ∗ \alpha^∗_i αi∗: (我们将展示最佳解决方案 α i ∗ \alpha^∗_i αi∗可以有效地找到并纳入社会推荐,以下等式可通过(12)中所有非零项 α i ∗ \alpha^*_i αi∗的平方和求和得到)
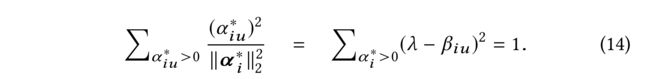
- We will show how the optimal solution α i ∗ \alpha^∗_i αi∗ can be efficiently found and be incorporated in social recommendation. The following equation can be obtained by squaring and summing both sides in (12) over all non-zero α i ∗ \alpha^∗_i αi∗: (我们将展示最佳解决方案 α i ∗ \alpha^∗_i αi∗可以有效地找到并纳入社会推荐,以下等式可通过(12)中所有非零项 α i ∗ \alpha^*_i αi∗的平方和求和得到)
-
(6) Through rewriting (14) in a quadratic form, we have (15): (通过以二次形式重写(14),我们得到)

-
(7) Thus, λ \lambda λ for user i i i can be calculated in (16) through solving (15). We note that we only keep the solution satisfying α i u ≥ 0 , ∀ u ∈ F ( i ) \alpha_{iu} \ge 0, \forall u \in F(i) αiu≥0,∀u∈F(i) (因此,可以通过求解(15)在(16)中计算用户 i i i的 λ \lambda λ。我们注意到,我们只会让解决方案满意)

-
(8) Therefore given k i ∗ k^∗_i ki∗, the optimal attention α i ∗ α^∗_i αi∗ can be obtained through substituting the computed value of λ \lambda λ by (16) into (10). Algorithm 1 presents the details for finding the optimal number k i ∗ k^∗_i ki∗ and optimal attention α i ∗ α^∗_i αi∗ for target user i i i. (因此给出了 k i ∗ k^∗_i ki∗ , 最佳注意 α i ∗ α^∗_i αi∗可通过将 λ \lambda λ的计算值代入(10)得到。算法1给出了寻找目标用户 i i i最优数 k i ∗ k^*_i ki∗的细节和最佳注意力 α i ∗ α^∗_i αi∗的细节。)

-
(9) Next we incorporate the concept of optimal limited attention into social recommendation through combining the optimal k ∗ k^∗ k∗ and α ∗ \alpha^∗ α∗ with matrix factorization. Generally, we estimate user i i i’s rating on item j j j, R i j R_{ij} Rij, through the dot product of social factor ϕ i \phi_i ϕi and item j j j’s latent feature vector V j V_j Vj: (接下来,我们将最优有限注意的概念结合到社会推荐中,通过在矩阵分解中结合 k ∗ k^∗ k∗ and α ∗ \alpha^∗ α∗ )

-
(10) Thus, we keep R i j R_{ij} Rij and ϕ i T V j \phi^T_iV_j ϕiTVj close to each other through minimizing the square loss shown in (18): (通过最大限度地减少图中所示的平方损失,彼此接近)
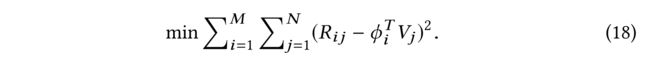
-
(11) Besides, given the additional social information for user i i i, we also hope that U i U_i Ui is close to ϕ i \phi_i ϕi and ϕ i \phi_i ϕi in turn is close to ∑ u ∈ F ( i ) k ∗ α i u U u \sum_{u \in F(i)_{k^*}} \alpha_{iu}U_u ∑u∈F(i)k∗αiuUu as well: (此外,考虑到用户ii的额外社交信息,我们也希望用户i 靠近 ϕ i \phi_i ϕi, ϕ i \phi_i ϕi反过来又去接近 ∑ u ∈ F ( i ) k ∗ α i u U u \sum_{u \in F(i)_{k^*}} \alpha_{iu}U_u ∑u∈F(i)k∗αiuUu)


- where we denote F ( i ) k ∗ F(i)_{k^∗} F(i)k∗ as the set of user i i i’s k i ∗ k^∗_i ki∗best influential friends and α i u ∗ α^∗_{iu} αiu∗ as the optimal attention from i i i to u u u.
-
(12) Putting (18) (19) and (20) together, our objective function is: (其中我们表示 F ( i ) k ∗ F(i)_{k^∗} F(i)k∗作为用户 i i i的 k i ∗ k^∗_i ki∗最好的有影响力的朋友,且 α i u ∗ α^∗_{iu} αiu∗是从用户 i i i到 u u u的最佳注意力。把(18)(19)和(20)放在一起,我们的目标函数是)
-
where ∑ U i T U i \sum U^T_iU_i ∑UiTUi and ∑ V j T V j \sum V^T_j V_j ∑VjTVjare regularization terms preventing overfitting.
- I i j R I^R_{ij} IijR is the indicator function that equals to 1 if user i i i has rated item j j j and equals to 0 otherwise.
-
(13) Assuming the optimal k i ∗ k^∗_i ki∗ and attention α i u ∗ α^∗_{iu} αiu∗ for user i i i are known, a local minimum of (21) can be found by taking the derivative and performing gradient descent on U i U_i Ui, V j V_j Vj, ϕ i \phi_i ϕi separately. The corresponding partial derivatives are shown as follows: (假设最优 k i ∗ k^∗_i ki∗和注意力 α i u ∗ \alpha^∗_{iu} αiu∗对于已知的用户 i i i,分别在 U i U_i Ui, V − j V-j V−j, ϕ i \phi_i ϕi上通过取导数并执行梯度下降,可以找到(21)的局部最小值,相应的偏导数如下所示:)
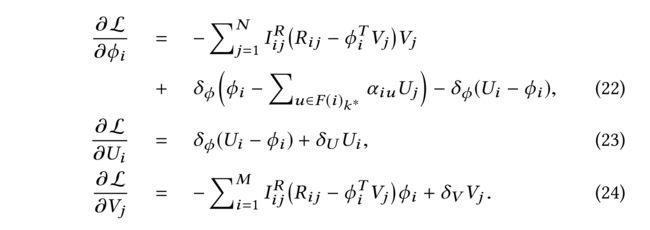
-
(14) We close this section by presenting the whole picture of our proposed OLA-Rec model. We employ an Expectation-Maximization (EM) [6] style optimization strategy to alternatively learn the parameters k ∗ k^∗ k∗, α ∗ α^∗ α∗, ϕ ϕ ϕ, U U U, V V V that minimize L \mathcal{L} L. (我们通过展示我们提出的OLA Rec模型的全貌来结束本节。我们采用期望最大化(EM)[6]式优化策略来交替学习参数 k ∗ k^∗ k∗, α ∗ α^∗ α∗, ϕ ϕ ϕ, U U U, V V V使 L \mathcal{L} L最小化的。)
E-step.
In each iteration, the optimal number k ∗ k^∗ k∗ and optimal attention α ∗ α^∗ α∗ for each user are calculated based on the current ϕ \phi ϕ and U U U through employing Algorithm 1. (在每次迭代中,每个用户的最优数 k ∗ k^∗ k∗ 最佳注意力 α ∗ \alpha^∗ α∗通过采用算法1,基于当前 ϕ \phi ϕ和 U U U,计算得到)
M-step.
Given the optimal k ∗ k^∗ k∗ and α ∗ α^∗ α∗ obtained from E-step , ϕ \phi ϕ, U U U, V V V are updated using standard gradient descent: (给定最优 k ∗ k^∗ k∗和 α ∗ α^∗ α∗E-step中获得, ϕ \phi ϕ, U U U, V V V使用标准梯度下降进行更新:)

-
where η \eta η is the learning rate and x ∈ { U , V , ϕ } x \in \{U,V, \phi\} x∈{U,V,ϕ} denotes any model parameter.(学习率 任何模型参数)
-
(15) Finally, the whole procedure terminates when the absolute difference between the losses in two consecutive iterations is less than 10−5. (最后,当两个连续迭代中损失的绝对差值小于 1 0 − 5 10^{-5} 10−5时,整个过程终止.)
-
(16) We close this section by pointing out that the concept of limited attention is a well-studied cognitive factor in social science which claims only a small portion of information can be processed in real time by each individual due to her limited mind strength. (我们在结束本节时指出,有限注意力的概念是社会科学中一个经过充分研究的认知因素,它声称由于每个人有限的思维能力,只有一小部分信息可以被实时处理)
- People nowadays with online social networks are much easier to get connected than before, especially for those who are not close enough to become friends off-line. This results in the problem that many of our friends on social networks may produce noisy/useless information. (通过一个数学模型和理论分析,在社会推荐中巧妙地引入有限注意的概念,我们最优地找到了最有用朋友的子集及其相应的注意权重,以同时解决上述问题)
- By elegantly introducing the concept of limited attention in social recommendation through a mathematical model with theoretical analyses, we optimally find a subset of most useful friends as well as their corresponding attention weights to solve the above problems simultaneously. (如今,拥有在线社交网络的人比以前更容易获得联系,尤其是那些关系不够亲密,无法在网上成为朋友的人。这导致了一个问题,即社交网络上的许多朋友可能会产生嘈杂/无用的信息。)
- In the following section, we will show that our solution is adequate to help boost recommendation performance through extensive experiments. (在下一节中,我们将通过大量实验证明我们的解决方案足以帮助提高推荐性能。)
4 EMPIRICAL EV ALUATION
In this section, we compare our proposed algorithm (OLA-Rec) with several state-of-the-art methods on four real-world datasets to demonstrate the superiority of OLA-Rec model over the others with respect to various evaluation metrics.
4.1 Experimental Setup
4.1.1 Evaluation Metrics.
-
The following metrics are used to measure the recommendation accuracy.
-
(1) Mean Absolute Error (MAE).

- where R i j R_{ij} Rij , R ^ i j \hat{R}_{ij} R^ij and N are the original rating, predictive rating and the number of ratings in test set.
-
(3) Recall@K.
This metric quantifies the fraction of consumed items that are in the top-K ranking list sorted by their estimated rankings. For each user u u u we define S ( K ; u ) S(K;u) S(K;u) as the set of already-consumed items in the test set that appear in the top-K list and S ( u ) S(u) S(u) as the set of all items consumed by this user in the test set. Then, we have (该指标量化了按估计排名排序的top-K排名列表中已消费物品的比例。对于每个用户 u u u,我们将 S ( K ; u ) S(K;u) S(K;u)定义为测试集中出现在top-K列表中的已消费项目集,将 S ( u ) S(u) S(u)定义为该用户在测试集中消费的所有项目集。那么,我们有)

-
(4) Precision@K.
This measures the fraction of the top-K items that are indeed consumed by the user (test set): (这测量了用户实际消费的top-K项目的分数(测试集):)
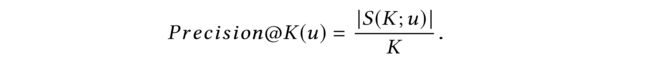
4.1.2 Datasets.
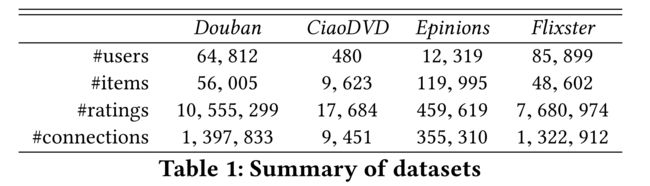
Our experiments are performed on four real-world datasets whose detailed filtering information will be presented in Appendix A. Table 1 gives a summary about their basic statistics. (我们的实验是在四个真实世界的数据集上进行的,这些数据集的详细过滤信息将在附录A中给出。表1总结了它们的基本统计数据。)
4.1.3 Comparable Approaches.
The following seven recommendation methods including our proposed OLA-Rec model are compared. (比较了以下七种推荐方法,包括我们提出的OLA Rec模型。)
- OLA-Rec. The proposed OLA-Rec model.
- TrustMF. The method capable of handling trust propagation, originally proposed by Yang et al. [40]. (该方法能够处理 信任传播,最初由Yang等人提出[40]。)
- SoReg. The individual-based regularization model with Pearson Correlation Coefficient (PCC) proposed in [20], which outperforms its other variants. ([20]中提出的 基于个体的 皮尔逊相关系数(PCC)正则化模型 优于其他变量。)
- SMF. This model [12] assumes that users’ latent feature factors are dependent on their ties’. (该模型[12]假设用户的潜在特征因素取决于他们的关系。)
- STE. The model proposed by Ma et al. [18] which aggregates a user’s own rating and her friends’ ratings to predict the target
user’s final rating on an item. (Ma等人[18]提出的模型将用户自己的评分和她朋友的评分相加,以预测目标用户对某个项目的最终评分。) - SoRec. The probabilistic matrix factorization model proposed by Ma et al. [19] which factorizes user-item rating matrix and
user-user linkage matrix simultaneously. (Ma等人[19]提出的概率矩阵分解模型同时分解用户项目评分矩阵和用户链接矩阵。) - PMF. The classic probabilistic matrix factorization model first proposed in [23]. (经典的概率矩阵分解模型首次在[23]中提出。)
4.2 Experimental Results
In Table 2, we show the performances of the above seven comparative models on four datasets, in terms of RMSE, MAE, Precision@5 (Pre@5) and Recall@5 (Rec@5). We conduct paired difference tests for two ranking metrics, Pre@5 and Rec@5, and ∗ indicates the significance of testing results at p < 0.05 with degree of freedom as # users - 1 on each dataset. (在表2中,我们展示了上述七个比较模型在四个数据集上的性能,即RMSE、MAE、,Precision@5 (Pre@5)及Recall@5 (Rec@5).我们对两个排名指标进行配对差异测试,Pre@5和Rec@5和∗ 表明测试结果在p<0.05时的显著性,每个数据集的自由度为#用户-1。)

-
(1) RMSE and MAE.
- As for RMSE and MAE, we observe that social recommendation models including SoRec, STE, SMF, SoReg and TrustMF benefit from taking extra social network information into account and therefore outperform vanilla matrix factorization based collaborative filtering model such as PMF. This result confirms the assumption in social recommendation literature that social information does help boost the accuracy of traditional recommendation methods. (至于RMSE和MAE,我们观察到包括SoRec、STE、SMF、SoReg和TrustMF在内的社交推荐模型从考虑额外的社交网络信息中获益,因此优于基于普通矩阵分解的协同过滤模型,如PMF。这一结果证实了社会推荐文献中的假设,即社会信息确实有助于提高传统推荐方法的准确性。)
- Besides, we can also observe from Table 2 that our proposed OLA-Rec model clearly beats all other methods on all datasets for both metrics, demonstrating the advantage of joint optimization in learning users’ latent preferences and finding the optimal number of their best influential social connections as well as obtaining the optimal corresponding attentions towards these chosen social connections. We note that due to the randomness in data splitting, model initialization and even data preprocessing, our results for some baselines may not be exactly the same as reported in the original works, though given our best efforts to diminish the variances. (此外,我们还可以从表2中观察到,我们提出的OLA Rec模型在两个指标的所有数据集上明显优于所有其他方法,展示了联合优化在学习用户潜在偏好、寻找其最佳有影响力的社会关系的最佳数量以及获得对所选社会关系的最佳对应关注方面的优势。 我们注意到,由于数据分割、模型初始化甚至数据预处理的随机性,我们对一些基线的结果可能与原始工作中报告的结果不完全相同,尽管我们尽了最大努力来减少差异。)
-
(2) Pre@5 and Rec@5.
- As for Pre@5 and Rec@5, we observe from Table 2 that our proposed OLA-Rec model significantly outperforms several baselines on almost every dataset, demonstrating its superiority over other state-of-the-art methods. For instance, the performance of OLA-Rec is roughly 9 times and 7 times better than PMF in terms of Rec@5 and Pre@5 on Douban, 6 times better and 3 times better than TrustMF in terms of Rec@5 and Pre@5 on Epinions. (至于Pre@5和Rec@5,我们从表2中观察到,我们提出的OLA Rec模型在几乎每个数据集上都显著优于几个基线,表明其优于其他最先进的方法。例如,OLA Rec的性能大约是PMF的9倍和7倍Rec@5和Pre@5在豆瓣上,与TrustMF相比,豆瓣的性能分别提高了6倍和3倍Rec@5和Pre@5在Epinions上。)
-
(3) Precision v.s. Recall.
- In Figure 1, we draw the Precision (Y-axis) vs. Recall (X-axis) curves of all seven recommendation methods for comparison. Data points from left to right on each line were calculated at different values of K, ranging from 5 to 50. The closer the line is to the top right corner, the better the algorithm is, indicating that both precision and recall are high. We observe from Figure 1 that OLA-Rec with no doubt achieves better performances than all other methods. Further, Figure 1 also confirms the trade-off between precision and recall —- as K increases, precision tends to go down while recall moves toward the opposite direction. (在图1中,我们绘制了所有七种推荐方法的精度(Y轴)与召回率(X轴)曲线,以进行比较。在不同的K值(从5到50)下,从左到右计算每条线上的数据点。直线越靠近右上角,算法就越好,这表明精确度和召回率都很高。我们从图1中观察到,OLA Rec无疑比所有其他方法获得了更好的性能。此外,图1还证实了精确性和召回率之间的权衡——随着K的增加,精确性趋于下降,而召回率则朝相反的方向移动。)
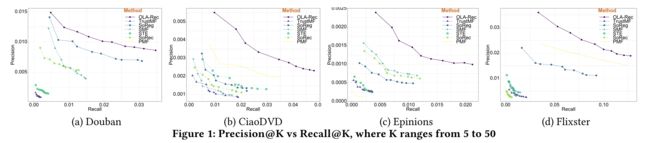
- In Figure 1, we draw the Precision (Y-axis) vs. Recall (X-axis) curves of all seven recommendation methods for comparison. Data points from left to right on each line were calculated at different values of K, ranging from 5 to 50. The closer the line is to the top right corner, the better the algorithm is, indicating that both precision and recall are high. We observe from Figure 1 that OLA-Rec with no doubt achieves better performances than all other methods. Further, Figure 1 also confirms the trade-off between precision and recall —- as K increases, precision tends to go down while recall moves toward the opposite direction. (在图1中,我们绘制了所有七种推荐方法的精度(Y轴)与召回率(X轴)曲线,以进行比较。在不同的K值(从5到50)下,从左到右计算每条线上的数据点。直线越靠近右上角,算法就越好,这表明精确度和召回率都很高。我们从图1中观察到,OLA Rec无疑比所有其他方法获得了更好的性能。此外,图1还证实了精确性和召回率之间的权衡——随着K的增加,精确性趋于下降,而召回率则朝相反的方向移动。)
-
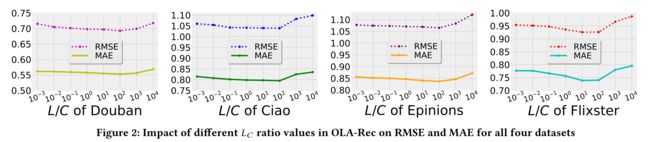
(4) Impact of L C L_C LC Ratio.
- We next discuss the impact of L C L_C LC ratio (L_C= L/C) in (9) on the performances of OLA-Rec. We can tell that LC controls the value of β i u β_iu βiu in (9), which in turn affects the calculation of λ \lambda λ in (16) and therefore indirectly influences the value of k k k. (接下来我们将讨论 L C L_C LC的影响(9)中的比值( L C L_C LC=L/C)对OLA-Rec的性能有影响。我们可以看出, L C L_C LC控制着 β i u β_{iu} βiu的值(9)中的,这反过来影响(16)中 λ \lambda λ的计算,因此间接影响 k k k的值。)
- When quite a small L C L_C LC is adopted, k k k tends to be very large, indicating that information from a large number of the target user’s friends (all of her friends in the extreme case) is considered to infer the target user’s preference. (当一个相当小的 L C L_C LC如果采用, k k k往往非常大,这表明来自目标用户的大量朋友(极端情况下是她的所有朋友)的信息被认为是推断目标用户偏好的信息。)
- Extremely, we may simply take every friend of the target user into account, ignoring the factor of limited attention. When L C L_C LC is very large, the target user’s taste will merely depend on very few friends (none of her friends in the extreme case). Figure 2 displays the performances of OLA-Rec with different L C L_C LC ratio values. (极端情况下,我们可能会简单地考虑目标用户的每个朋友,忽略注意力有限的因素。当 L C L_C LC是非常大的,目标用户的品味将只取决于很少的朋友(在极端情况下没有她的朋友)。图2显示了具有不同 L C L_C LC的OLA Rec的性能比值。)
- We observe that for all of the four datasets, as L C L_C LC increases, RMSE and MAE first decrease (prediction accuracy increases) and then increase (prediction accuracy decreases) after L C L_C LC goes beyond a certain threshold whose value is 100 for Douban, CiaoDVD, Epinions and 10 for Flixster. This confirms our intuition that by finding an optimal number of best influential friends for each user and learning their optimal attentions received from the target user, OLA-Rec is able to achieve a performance boost over models purely utilizing information from every friend without considering limited attention and models simply ignoring any social information. (我们观察到,对于所有四个数据集,在 L C L_C LC增加之后,RMSE和MAE先降低(预测精度增加),然后增加(预测精度降低)超过某个阈值,豆瓣、CiaoDVD、Epinions的值为100,Flixster的值为10。这证实了我们的直觉,即通过为每个用户找到最佳数量的最有影响力的朋友,并了解他们从目标用户那里得到的最佳关注,OLA Rec能够在完全利用每个朋友的信息的模型上实现性能提升,而无需考虑有限的注意力,模型只需忽略任何社交信息。)
-
(5) Histograms on k ∗ n \frac{k^∗}{n} nk∗.
- It is obvious that the upper bound of k i ∗ k^∗_i ki∗ is ∣ F ( i ) ∣ |F(i)| ∣F(i)∣ which is the size of user i i i’s total social connections. Therefore it is worth comparing the optimal number of selected social ties (denoted as k ∗ k^∗ k∗) with the exact number of total social ties (denoted as n n n) in the experiments. Figure 3 presents the histograms over k ∗ n \frac{k^∗}{n} nk∗ for users on each dataset. We observe a skewed distribution on each of the four datasets, showing that the majority of the population select between 70% and 100% of their social connections as social information sources. Furthermore, the histograms over total number of social connections are given in Figure 4, demonstrating a skewed distribution on each dataset as well. The combination of Figure 3 and Figure 4 provides us with two indications: (显然, k i ∗ k^*_i ki∗的上界是 ∣ F ( i ) ∣ |F(i)| ∣F(i)∣这是用户 i i i的总社交关系的大小。因此,值得比较所选社交关系的最佳数量(表示为 k ∗ k^* k∗) 与实验中总的社会关系(表示为 n n n)的确切数量。图3显示了 k ∗ n \frac{k^∗}{n} nk∗上的直方图表示每个数据集上的用户。我们观察到四个数据集中的每一个都有一个偏态分布,表明大多数人选择70%到100%的社会关系作为社会信息源。此外,图4给出了社会联系总数的直方图,显示了每个数据集上的偏态分布。图3和图4的组合为我们提供了两个指示:)
- (1) Most users in practice only need social information from a subset of their total social connections (i.e., k ∗ n \frac{k^∗}{n} nk∗) when making recommendations to them. (在实践中,大多数用户只需要他们全部社会关系的一个子集(即 k ∗ n \frac{k^∗}{n} nk∗<1)向他们提出建议时。)
- (2) Users with a larger number of social connections tend to have a smaller k ∗ n \frac{k^∗}{n} nk∗ and vice versa. This actually makes sense because having a large number of social connections may produce noisy information that has negative impact on inferring the preferences of these target users. (拥有大量社交网络的用户往往拥有较少的社交网络 k ∗ n \frac{k^∗}{n} nk∗ 反之亦然。这实际上是有道理的,因为拥有大量的社会关系可能会产生嘈杂的信息,对推断这些目标用户的偏好产生负面影响。)
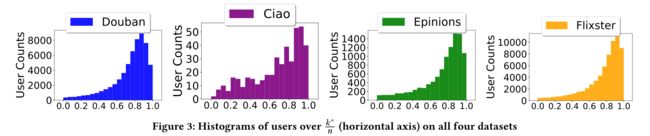

- (3) We remark that it is possible to use all the social connections when necessary, which actually is not a ”bad” choice. The contribution of our work is that for each user we can find an optimal subset (size k∗ ∈ [1, n], with theoretical guarantee) of her social ties who contribute in affecting her preference without any useful social information loss through an elegant combination of motivation from social science and formulation from math. In fact,our model is expected to reduce useless/noisy social information when k∗< n, which happens for over 80% of the users having more than 15 social ties. (我们注意到,在必要时可以使用所有的社会关系,这实际上不是一个“坏”的选择。我们工作的贡献在于,对于每个用户,我们都可以找到一个最优子集(大小 k ∗ ∈ [ 1 , n ] k^∗ \in [1,n] k∗∈[1,n],从理论上保证)她的社会关系通过社会科学的动机和数学公式的巧妙结合,在不损失任何有用的社会信息的情况下影响她的偏好。实际上,当 k ∗ < n k^* < n k∗<n、 超过80%的用户拥有超过15种社交关系。)
-
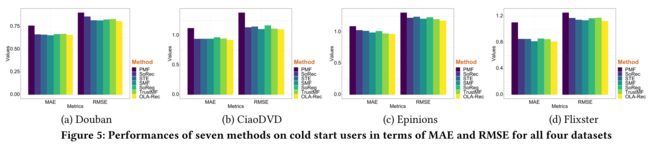
(6) Cold Start Problem.
- (1) Last but not least, we drill down to the performances of different algorithms on cold-start users. As is common practice, we define users rating less than five items as cold-start users. Figure 5 depicts the performances of various methods on cold start users. (最后,我们深入研究了不同算法在冷启动用户上的性能。按照惯例,我们将评分低于五项的用户定义为冷启动用户。图5描述了各种方法在冷启动用户上的性能。)
- (2) Our observations that social recommendation methods (including SoRec, STE, SMF, SoReg, TrustMF and OLA-Rec) significantly outperform PMF (a non-social algorithm) in terms of both MAE and RMSE in Figure 5 confirm the fact that social recommendation methods are superior to their non-social competitors particularly for cold-start users. (我们在图5中观察到,社交推荐方法(包括SoRec、STE、SMF、SoReg、TrustMF和OLA Rec)在MAE和RMSE方面显著优于PMF(一种非社交算法),这证实了一个事实,即社交推荐方法优于其非社交竞争对手,尤其是对于冷启动用户。)
- We also observe that our OLA-Rec model have similar accuracies in terms of both MAE and RMSE to the other social recommendation baselines. This may due to the reason that when the target user processes a very small number of social connections, the diversity of these social ties reduces dramatically, making the proposed OLA-Rec model simply take all social connections into account to obtain as much useful information as possible. (我们还观察到,我们的OLA Rec模型在MAE和RMSE方面的精确度与其他社会推荐基线类似。这可能是因为当目标用户处理极少量的社会关系时,这些社会关系的多样性会显著降低,这使得拟议的OLA Rec模型只考虑所有社会关系,以获得尽可能多的有用信息。)
- In this case, given exactly the same amount of social information shared by all social recommendation methods, the credit of slightly better performances obtained by OLA-Rec may go to learning the optimal attentions (i.e., α i ∗ α^∗_i αi∗) for each target user i i i. (在这种情况下,考虑到所有社会推荐方法共享的社会信息量完全相同,OLA Rec获得的稍好的性能可以归功于学习最佳注意(即 α i ∗ \alpha^*_i αi∗) 对于每个目标用户 i i i。)
5 CONCLUSIONS
- (1) Limited attention is very important to social recommendation as it has been proved to have significant impact on users’ online behaviours. (有限的关注对社交推荐非常重要,因为事实证明它对用户的在线行为有重大影响。)
- Therefore, we propose to incorporate limited attention, a well-studied social science notion into social recommendation in an appropriate way. (因此,我们建议以适当的方式将有限的注意力、经过充分研究的社会科学概念纳入社会推荐中。)
- We first formulate the optimal limited attention problem, aiming to optimally bring the concept of limited attention into social recommendation. (我们首先提出了最优有限注意问题,旨在将有限注意的概念最优地引入到社会推荐中。)
- Then we develop a novel model which efficiently finds an optimal number of friends whose preferences have the best impact on the target user and adaptively learns an optimal personalized attention towards every selected friend, as well as the latent preference for each user. (然后,我们开发了一个新的模型,该模型可以有效地找到对目标用户的偏好影响最大的最佳朋友数,并自适应地学习对每个选定朋友的最佳个性化注意,以及每个用户的潜在偏好。)
- We also provide a proof on the optimality of the proposed algorithm. Extensive experiments on four real-world datasets demonstrate the improvement of our proposed method over existing approaches. (我们还证明了该算法的最优性。在四个真实数据集上的大量实验表明,我们提出的方法比现有方法有了改进。)
ACKNOWLEDGMENTS
REFERENCES
A SUPPLEMENT
Datasets.
-
Douban. This is a public dataset from a Chinese movie forum (http://movie.douban.com/), containing user-user friendships and user-movie ratings, and is publicly available from (https: //www.cse.cuhk.edu.hk/irwin.king.new/pub/data/douban). (豆瓣。这是一个来自中国电影论坛的公共数据集(http://movie.douban.com/),包含用户友谊和用户电影评分,可从以下网址公开获取(https://www.cse.cuhk.edu.hk/irwin.king.new/pub/data/douban)。)
-
CiaoDVD.The trust relationships among users from CiaoDVD as well as their ratings on DVDs are included. It was crawled from the entire category of DVDs of a UK DVD community website (http://dvd.ciao.co.uk) in December, 2013. (包括CiaoDVD用户之间的信任关系以及他们在DVD上的评级。它是从英国DVD社区网站的整个DVD类别中抓取的(http://dvd.ciao.co.uk)2013年12月。)
-
Epinions. This dataset comes from an American website and consists of trust relationships and user-item ratings. This dataset (http://www.trustlet.org/wiki/Epinions_dataset) is extracted from the consumer review website Epinions (http://www.epinions.com/), which contains user-user trust relationships and numerical ratings. (该数据集来自一家美国网站,由信任关系 和 用户项目评级 组成。这个数据集(http://www.trustlet.org/wiki/Epinions_dataset)摘自消费者评论网站Epinions(http://www.epinions.com/),其中包含用户信任关系和数字评级。)
-
Flixster.This dataset (http://www.cs.ubc.ca/~jamalim/datasets/) contains the information of user-movie ratings as well as user-user friendships from Flixster, an American social movie site for discovering new movies (http://www.flixster.com/). (这个数据集(http://www.cs.ubc.ca/~jamalim/datasets/)包含用户电影评级的信息,以及来自Flixster的用户友谊信息。Flixster是一个美国社交电影网站,用于发现新电影(http://www.flixster.com/).)
-
We remove users with less than 2 ratings and select 80% of each user’s ratings at random for training, leaving the remainder as test set. (我们删除评分低于2的用户,并随机选择每个用户评分的80%进行训练,剩下的作为测试集。)
B PROOF OF EQUATION (7)
Theorem B.1. (Hoeffding’s Inequality).
- Let { x j } j = 1 n ∈ [ L j , U j ] n \{x_j\}^n_{j=1} \in [L_j, U_j]^n {xj}j=1n∈[Lj,Uj]n be a sequence of independent random variables, such that E [ x j ] = µ j E[x_j] = µ_j E[xj]=µj. Then, it holds that: (是一系列独立的随机变量)

- (2) We want to prove that by Hoeffding’s inequality, with probability at least 1 − δ \delta δ, we have : ( 我们想用霍夫丁不等式证明,概率至少为1− δ \delta δ,我们有)

- where ∣ ϵ j ∣ ≤ b |\epsilon_j| \le b ∣ϵj∣≤b for some b ≥ 0 b \ge 0 b≥0 and E [ ϵ j ] = 0 E[\epsilon_j] = 0 E[ϵj]=0. We further constrain α i j ≥ 0 \alpha_{ij} \ge 0 αij≥0 and ∑ j = 1 ∣ F ( i ) ∣ α i j = 1 \sum^{|F(i)|}_{j=1}α_{ij} = 1 ∑j=1∣F(i)∣αij=1.
Proof.
- Given x j = α i j ϵ j x_j = \alpha_{ij} \epsilon_j xj=αijϵj, we have:

- and thus:

- Let n = ∣ F ( i ) ∣ n = |F(i)| n=∣F(i)∣ and x = C ∥ α i ∥ 2 x = C∥\alpha_i∥_2 x=C∥αi∥2, we have:

- Recall that − b ≤ ϵ j ≤ b −b \le \epsilon_j \le b −b≤ϵj≤b and therefore L j = − b ∗ α i j L_j = −b ∗ \alpha_{ij} Lj=−b∗αij and U j = b ∗ α i j U_j = b ∗ \alpha_{ij} Uj=b∗αij. Thus we have:
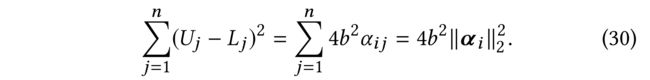
- Substitute Eq (30) into Eq (29), we have: (将等式(30)替换为等式(29),我们得到)

- By rewriting Eq (31), we finally get:

- which completes the proof.