【因果推断与机器学习】Causal_inference: Chapter 4
Chapter4: Estimation
一旦我们找到了识别因果量的策略,我们就需要选择如何使用统计方法估计这些因果量。我们使用受实际计算应用程序启发的示例来描述最常用的方法。首先,我们介绍因果估计的基础知识:如何从已确定的估计值到估计器?我们描述了在每种估计方法中都需要权衡的偏差和方差的挑战。其次,我们提出了各种估计方法,从简单的、可解释的估计器到复杂的基于机器学习的估计器,当数据是高维时通常需要的。
4.1 Example: Building an estimator
在上一章节中,我们看到识别是将因果效应转化为统计量的过程,称为识别的估计量。识别后Estimate是使用数据计算此量化效应的过程。
4.1.1 Estimating causal effect of ice-cream consumption
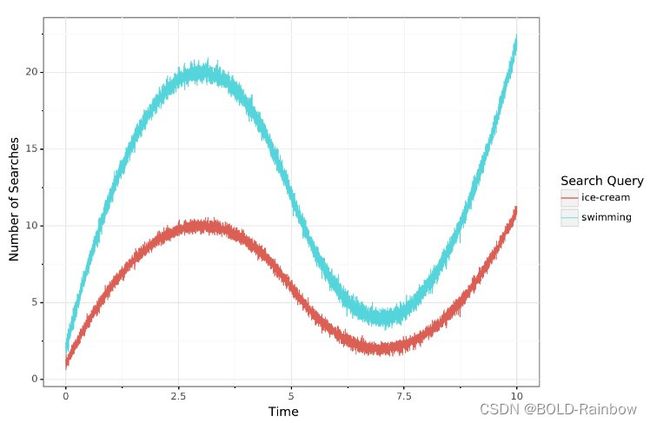
假设您有权访问向热门搜索引擎发出的搜索查询的匿名数据。进一步假设您是冰淇淋的学者,并希望了解其对不同健康结果的影响。你的同事与你分享了一个有趣的观察结果:“我可以在哪里吃冰淇淋”的搜索查询数量与“我可以在哪里游泳”的搜索查询数量高度相关。他们问你,这是否意味着吃冰淇淋会让人们更容易想游泳?图1绘制了两个搜索查询随时间的变化。
观察证据相当有力,但你可能会怀疑。在第1章中,我们看到温度可能是一个混杂因素,因此我们应该解释它。第3章通过引入后门标准,提供了这样做的正确方法。具体来说,假设没有其他混杂因素,因果关系是:
E [ s w i m ∣ d o ( i c e c r e a m ) ] = ∑ t e m p E [ s w i m ∣ i c e c r e a m , t e m p ] P ( t e m p ) (1) E[swim|do(icecream)]\: =\: \sum_{temp}E[swim|icecream,temp]P(temp) \\ \quad \tag{1} E[swim∣do(icecream)]=temp∑E[swim∣icecream,temp]P(temp)(1)
其中游泳和冰淇淋分别对应于游泳和冰淇淋的查询数量,温度是当时的温度。有多种方法可以估计上述数量。其中一种方法是离散化icecream和temp并计算对于给定的icecream和temp值的情况下,游泳对这两个变量的效应。让icecream二值化为**{High,Low}** 温度离散化为 {Low, Medium, High}.然后可以使用以下两个等式来估计因果效应:
E [ s w i m ∣ i c e c r e a m = i c , t e m p = t e ] = 1 N t e , i c ∑ t e m p = t e , i c e c r e a m = i c s w i m P r ( t e m p ) = N t e N (2) \begin{align} \mathbb{E}[swim|icecream=ic,temp=te] \: &= \: \frac{1}{N_{te,ic}}\sum_{temp=te,\\icecream=ic} swim\\ Pr(temp)\: &= \: \frac{N_{te}}{N}\\ \end{align} \tag{2} E[swim∣icecream=ic,temp=te]Pr(temp)=Nte,ic1temp=te,icecream=ic∑swim=NNte(2)
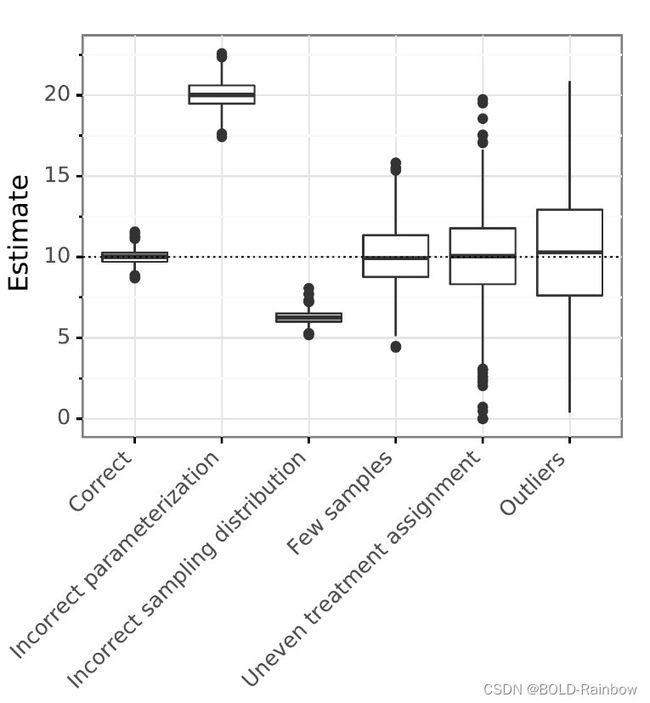
只要每个条件均值都可以可靠地估计,上述估计效果很好。当特定温度和冰淇淋查询桶的数据很少时会发生什么?表1给出了这样一个数据集,很少有人在低温下搜索冰淇淋。数据集中的每个条目都是一个连续的时间段,具有低温、中温度或高温。对于每个条目,数据集按级别提供冰淇淋查询的频率和游泳查询的数量。如果我们应用方程1,2,我们就获得了冰淇淋搜索对游泳的积极影响。但显然我们知道事实并非如此。罪魁祸首是从非常小的样本(在本例中为单个数据点)估计平均值。一个可能的解决方法是从低温中排除数据,并计算中高温下的影响。然而,我们的新估计不再对应于所有温度:根据数据,我们不能说冰淇淋在低温下的影响。
该示例说明了从数据中估计因果数量的挑战,即使使用直接确定的估计值也是如此。虽然我们展示了一个具有单个离散混杂器的示例,但是当混杂子是多维的并且当它们连续时不可避免时,混杂子的特定值的低频场景更有可能发生。如何对高维混杂因素进行条件分析是因果估计方法的关键问题之一。
表1:搜索不同时间点的冰激凌查询次数以及相关温度值。每行对应一个特定的(温度、冰激凌查询次数)。有些组合很少见:当温度较低时,只有一个时间段的冰淇淋查询数量很高。最右边的列显示同一时间段内的平均游泳查询。
| 温度 | 冰激凌查询次数 | 频率 | 平均游泳查询次数 |
|---|---|---|---|
| 低 | 低 | 9999 | 505 |
| 低 | 高 | 1 | 560 |
| 中等 | 低 | 5000 | 2151 |
| 中等 | 高 | 5000 | 2150 |
| 高 | 低 | 1000 | 4750 |
| 高 | 高 | 9000 | 4751 |
4.12 Estimating causal effect using a randomized experiment
如果我们能够创建自己的数据,则上述许多估计挑战都可以解决。让我们随机选择一个城市中的人样本,并将他们分为两组:一组每天提供冰淇淋,持续一周,另一组提供其他小吃。然后,我们可以在一周内跟踪他们的游泳活动(或搜索游泳)。这创建了一个随机实验,其中治疗是冰淇淋,结果是游泳活动。从第3章开始,我们知道在随机实验中确定的估计值只是给定治疗结果的条件期望。有了这个估计值作为目标估计值和可用的实验数据,我们现在可以使用一个简单的插件估计器来估计这个量,而不必担心温度等混杂因素。
E [ Y ∣ d o ( T = t ) ] → E [ Y ∣ T = t ] → ∑ i = 1 N 1 T = t Y ∑ i = 1 N 1 T = t \mathbb{E}[Y|do(T=t)]\rightarrow \mathbb{E}[Y|T=t] \rightarrow \frac{\sum_{i=1}^{N}1_{T=t}Y} {\sum_{i=1}^{N}1_{T=t}}\\ E[Y∣do(T=t)]→E[Y∣T=t]→∑i=1N1T=t∑i=1N1T=tY
使用这个基本的估计器,我们现在可以估计感兴趣的不同因果量。最常用的是平均治疗效果(ATE)。当治疗是二元的时,ATE简化为:
A T E : = E [ Y ∣ d o ( T = 1 ) ] − E [ Y ∣ d o ( T = 0 ) ] → E [ Y ∣ T = 1 ] − E [ Y ∣ T = 0 ] → ∑ i = 1 N 1 T = 1 Y ∑ i = 1 N 1 [ T = 1 ] − ∑ i = 1 N 1 T = 0 Y ∑ i = 1 N 1 [ T = 0 ] \begin{aligned} ATE:&=\mathbb{E}[Y|do(T=1)]\: - \: \mathbb{E}[Y|do(T=0)]\\ &\rightarrow \mathbb{E}[Y|T=1]-\mathbb{E}[Y|T=0] \rightarrow \frac{\sum_{i=1}^{N}1_{T=1}Y}{\sum_{i=1}^{N}1_[T=1]}-\frac{\sum_{i=1}^{N}1_{T=0}Y}{\sum_{i=1}^{N}1_[T=0]} \end{aligned} ATE:=E[Y∣do(T=1)]−E[Y∣do(T=0)]→E[Y∣T=1]−E[Y∣T=0]→∑i=1N1[T=1]∑i=1N1T=1Y−∑i=1N1[T=0]∑i=1N1T=0Y
注意到,我们不需要担心温度或任何其他变量。在随机实验中,估计值只是提供冰淇淋的人和没有提供冰淇淋的人之间平均游泳活动的差异。
然而,有时我们可能只对特定人群的影响感兴趣,例如,属于特定人口统计或共享某些属性的人。由于治疗是随机的,这些属性与治疗无关,但可以与结果相关。这些属性称为“效果修饰符”和由此产生的估计,条件平均治疗效果,通常缩写为CATE。它可以使用相同的原理进行估计:确定因果数量,然后使用简单的估计器。
C A T E : = E [ Y ∣ d o ( T = 1 ) , C = c ] − E [ Y ∣ d o ( T = 0 ) , C = c ] → E [ Y ∣ T = 1 , C = c ] − E [ Y ∣ T = 0 , C = c ] → ∑ i = 1 N 1 [ T = 1 , C = c ] Y ∑ i = 1 N 1 [ T = 1 , C = c ] − ∑ i = 1 N 1 [ T = 0 , C = c ] Y s u m i = 1 N 1 [ T = 0 , C = c ] \begin{aligned} CATE: &=\mathbb{E}[Y|do(T=1),C=c]-\mathbb{E}[Y|do(T=0),C=c] \\ &\rightarrow \mathbb{E}[Y|T=1,C=c]-\mathbb{E}[Y|T=0,C=c] \\ &\rightarrow {{\sum_{i=1}^{N}1[T=1,C=c]Y} \over {\sum_{i=1}^{N}1[T=1,C=c]} } - {{\sum_{i=1}^{N}1[T=0,C=c]Y}\over {sum_{i=1}^{N}1[T=0,C=c]}} \\ \end{aligned} CATE:=E[Y∣do(T=1),C=c]−E[Y∣do(T=0),C=c]→E[Y∣T=1,C=c]−E[Y∣T=0,C=c]→∑i=1N1[T=1,C=c]∑i=1N1[T=1,C=c]Y−sumi=1N1[T=0,C=c]∑i=1N1[T=0,C=c]Y
4.1.3 Challenges in estimation with finite data
如果我们从随机实验中获得足够大的数据,那么像这样的简单估计器就足够了。然而,由于数据有限,从随机实验中估计目标估计仍然存在多种挑战(因此也适用于观察性研究)。例如,考虑一个随机实验,其中真正的因果效应在人与人之间差异很大。特别是,对少数人来说,真正的效果比其他人高出几个数量级。查看均值的差异
N
上述ATE样本,取决于这些偏远人群是否被分配治疗或对照,可能会影响所得的ATE。如果您再次运行实验,您可能会得到截然不同的结果!知道了这一点,就可以修剪所有记录的结果,使得高于某个阈值的结果被限制在阈值。这将使每个实验的结果更具可重复性,但我们现在遇到了一个不同的问题:由于这种任意的截止,我们不再估计目标估计值。
当治疗是连续的时,会出现一系列不同的挑战。也许最根本的是,治疗效果不再明确。当冰淇淋查询从 0 增加到 10 或从 100 增加到 101 时,我们是否估计游泳查询的变化?如果效果因不同的治疗值而异,我们报告哪一个?
最后,还有一个更普遍的问题,即搜索引擎用户是否代表底层人群。如果没有,我们可能会估计冰淇淋对搜索引擎用户的因果影响,但这可能不会推广到我们感兴趣的人群。也许搜索引擎的用户比一般人群更老,更健康或在某些方面不同?就像我们在第3章中定义了用于识别的治疗分配机制一样,抽样机制对于估计很重要。抽样机制是收集数据的过程,反过来,确定样本表示目标概率分布的程度。例如,通过仅从搜索引擎用户收集数据,所得到的数据可能不代表目标人群,即城市中的人们。
形式上,抽样机制定义了一个概率分布,从中独立地绘制可用的数据点。抽样分布与目标数据分布匹配的程度决定了数据的适宜性。因此,根据现有数据估计的任何数量仅对应于可以假定其随机抽样的特定抽样分布,除非可以假定现有数据代表一般总体。
The bias-variance tradeoff
我们上面的例子说明了统计估计器的偏差和方差之间的基本权衡。偏差对应于估计值预计接近已识别估计值的程度。如果多次运行试验,估计器的方差对应于估计值中的预期差值。
一般来说,减少方差(例如,通过删除上面示例中的异常值)会增加偏差,反之亦然。很难获得既具有低偏差又具有低方差的估计器。更复杂的是,对于一个数据集具有低偏差和低方差的估计器可能对不同的数据集具有非常不同的属性,因此通常没有普遍最好的估计器。
估计的目标是在偏差和方差之间找到令人满意的权衡。正式地,对于目标估计 h h h及其估计器 h ^ \hat{h} h^,偏差定义为目标估计值与预期值之间的差值 h ^ \hat{h} h^在多个独立样本上。方差定义为不同样本的估计值与均值估计值之间的平方差的预期值。
B i a s : = ∣ h − E [ h ^ ] V a r : = E [ ( h ^ − E [ h ^ ] ) 2 ] \begin{aligned} Bias:&=|h-\mathbb{E}[\hat{h}] \\ Var:&= \mathbb{E}[{(\hat{h}-\mathbb{E}[\hat{h}])^2}] \end{aligned} Bias:Var:=∣h−E[h^]=E[(h^−E[h^])2]