曲线拟合问题(手写高斯牛顿法/ceres/g2o)
曲线拟合问题 手写高斯牛顿法/ceres/g2o
- 矩阵求导术
-
- 曲线拟合
- 手写高斯牛顿
- ceres曲线拟合
- g2o曲线拟合
代码里面有详细的注释,可以结合代码来看
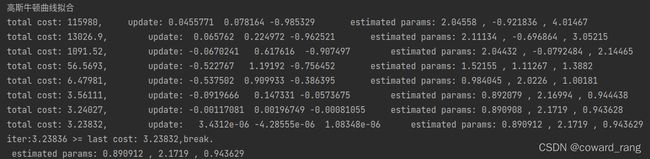
第一种方法是直接高斯牛顿来求的,套公式
第二种方法ceres ,同样定义出误差项,待优化变量就行,雅克比可求可不求,自己求的速度快,只需要重新实现里面的函数就行
第三种方法g2o,这里牵涉到定点与边的概念,顶点就是优化的量,边就是误差项,也可以自动求导,也可以重新实现自己求导
里面应该没有错误,要是有错误也是笔误,公式太难敲了
矩阵求导术
在讲解高斯牛顿前,首先讲一下矩阵求导,毕竟都是为了求极值,需要用到导数
令 A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] , x = ( x 1 ⋮ a n ) A= \begin{bmatrix} a_{11}& a_{12}& \cdots & a_{1n} \\ a_{21}& a_{22}& \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1}& a_{n2}& \cdots & a_{nn} \end{bmatrix} , x =\begin{pmatrix} x_{1} \\ \vdots \\ a_{n} \end{pmatrix} A=⎣⎢⎢⎢⎡a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann⎦⎥⎥⎥⎤,x=⎝⎜⎛x1⋮an⎠⎟⎞
则 A x = [ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n ⋮ a n 1 x 1 + a n 2 x 2 + ⋯ + a n n x n ] n ∗ 1 , 令 f ( x ) = ( f 1 ( x ) f 2 ( x ) ⋮ f n ( x ) ) Ax= \begin{bmatrix} a_{11}x_{1}+a_{12}x_{2}+\cdots+a_{1n}x_{n} \\ a_{21}x_{1}+a_{22}x_{2}+\cdots+a_{2n}x_{n} \\ \vdots \\ a_{n1}x_{1}+a_{n2}x_{2}+\cdots+a_{nn}x_{n} \\ \end{bmatrix}_{n*1},令 f(x) =\begin{pmatrix} f_{1}(x) \\ f_{2}(x) \\ \vdots \\ f_{n}(x) \end{pmatrix} Ax=⎣⎢⎢⎢⎡a11x1+a12x2+⋯+a1nxna21x1+a22x2+⋯+a2nxn⋮an1x1+an2x2+⋯+annxn⎦⎥⎥⎥⎤n∗1,令f(x)=⎝⎜⎜⎜⎛f1(x)f2(x)⋮fn(x)⎠⎟⎟⎟⎞
∂ f ( x ) ∂ x T = [ ∂ f 1 ( x ) ∂ x 1 ∂ f 1 ( x ) ∂ x 2 ⋯ ∂ f 1 ( x ) ∂ x 3 ∂ f 2 ( x ) ∂ x 1 ∂ f 2 ( x ) ∂ x 2 ⋯ ∂ f 2 ( x ) ∂ x 3 ⋮ ⋮ ⋱ ⋮ ∂ f n ( x ) ∂ x 1 ∂ f n ( x ) ∂ x 2 ⋯ ∂ f n ( x ) ∂ x 3 ] = ( a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ) = A \frac{\partial f(x)}{\partial x^{T}}= \begin{bmatrix} \frac{\partial f_{1}(x)}{\partial x_{1}}& \frac{\partial f_{1}(x)}{\partial x_{2}} &\cdots &\frac{\partial f_{1}(x)}{\partial x_{3}}\\ \frac{\partial f_{2}(x)}{\partial x_{1}}& \frac{\partial f_{2}(x)}{\partial x_{2}} &\cdots &\frac{\partial f_{2}(x)}{\partial x_{3}}\\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial f_{n}(x)}{\partial x_{1}}& \frac{\partial f_{n}(x)}{\partial x_{2}} &\cdots &\frac{\partial f_{n}(x)}{\partial x_{3}}\\ \end{bmatrix} =\begin{pmatrix} a_{11} & a_{12} &\cdots & a_{1n} \\ a_{21} & a_{22} &\cdots & a_{2n} \\ \vdots & \vdots &\ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix} =A ∂xT∂f(x)=⎣⎢⎢⎢⎢⎡∂x1∂f1(x)∂x1∂f2(x)⋮∂x1∂fn(x)∂x2∂f1(x)∂x2∂f2(x)⋮∂x2∂fn(x)⋯⋯⋱⋯∂x3∂f1(x)∂x3∂f2(x)⋮∂x3∂fn(x)⎦⎥⎥⎥⎥⎤=⎝⎜⎜⎜⎛a11a21⋮an1a12a22⋮an2⋯⋯⋱⋯a1na2n⋮ann⎠⎟⎟⎟⎞=A
所以 ∂ A x ∂ x T = A \frac{\partial Ax}{\partial x^{T}}= A ∂xT∂Ax=A
对于一个最小二乘的问题
x ∗ = a r g min 1 2 ∣ ∣ f ( x ) ∣ ∣ 2 ① \tag*{①}x^ {*} =arg \min \frac {1}{2} ||f(x) ||^ {2} x∗=argmin21∣∣f(x)∣∣2①
高斯牛顿的思想是把 f ( x ) f(x) f(x)泰勒展开,取一阶线性项近似:
f ( x + Δ x ) ≈ f ( x ) + f ′ ( x ) Δ x = f ( x ) + J ( x ) T △ x ② \tag*{②}f(x+ \Delta x) \approx f(x)+f'(x) \Delta x = f(x)+J(x)^{T} \triangle x f(x+Δx)≈f(x)+f′(x)Δx=f(x)+J(x)T△x②
将②式代入①式
1 2 ∥ f ( x + J ( x ) T Δ x ) ∥ 2 = 1 2 ( f ( x ) T f ( x ) + 2 f ( x ) T J ( x ) Δ x + Δ x T J ( x ) T J ( x ) Δ x ) \frac{1}{2}\left\|f(x+J(x)^{T}\Delta x) \right\|^{2} = \frac{1}{2}(f(x)^{T}f(x)+2f(x)^{T}J(x)\Delta x+\Delta x^{T}J(x)^{T}J(x)\Delta x) 21∥∥f(x+J(x)TΔx)∥∥2=21(f(x)Tf(x)+2f(x)TJ(x)Δx+ΔxTJ(x)TJ(x)Δx)
最后求得结果:
J ( x ) T J ( x ) Δ x = − J ( x ) T f ( x ) J(x)^ {T}J(x)\Delta x=-J(x)^ {T}f(x) J(x)TJ(x)Δx=−J(x)Tf(x)
备注:
1.这里求导的第①项与 Δ x \Delta x Δx无关,求导结果为0,
2.第②项 ( f ( x ) T J ( x ) Δ x ) ′ = J ( x ) T f ( x ) , (f(x)^{T}J(x)\Delta x)^{'} = J(x)^{T}f(x), (f(x)TJ(x)Δx)′=J(x)Tf(x),这个是根据上面的的矩阵求导 ∂ A x ∂ x = A T \frac{\partial Ax }{\partial x}=A^{T} ∂x∂Ax=AT得到的
3.第③项 Δ x T J ( x ) T J ( x ) Δ x = 2 J ( x ) T J ( x ) Δ x \Delta x^{T}J(x)^{T}J(x)\Delta x = 2J(x)^{T}J(x)\Delta x ΔxTJ(x)TJ(x)Δx=2J(x)TJ(x)Δx详情见手写的,不想敲公式了结论就是: d x T A x d x = ( A + A T ) x \frac{\mathrm{d} x^{T}Ax}{\mathrm{d} x} = (A+A^{T})x dxdxTAx=(A+AT)x,等有时间再敲… ( J ( x ) T J ( x ) ) T = J ( x ) T J ( x ) (J(x)^{T}J(x))^{T} =J(x)^{T}J(x) (J(x)TJ(x))T=J(x)TJ(x), 整体 J ( x ) T J ( x ) J(x)^{T}J(x) J(x)TJ(x)是反对称矩阵,
曲线拟合
拟合一条如下的曲线方程, w w w为高斯噪声,满足 w ( 0 , σ 2 ) w~(0,\sigma_{2}) w (0,σ2).
y = e x p ( a x 2 + b x + c ) + w y = exp(ax^{2}+bx+c)+w y=exp(ax2+bx+c)+w
有N个观测数据,构建一个最小二乘问题,
min a , b , c 1 2 ∑ i = 1 N ∥ y i − e x p ( a x i 2 + b x i + c ) ∥ \min_{a,b,c} \frac{1}{2} \sum_{i=1}^{N} \left \| yi-exp(ax_{i}^2+bx_{i}+c) \right \| a,b,cmin21i=1∑N∥∥yi−exp(axi2+bxi+c)∥∥
定义误差项 e i = y i − e x p ( a x i 2 + b x i + c ) ⇒ f ( x i ) = e i ei = yi-exp(ax_{i}^2+bx_{i}+c) \Rightarrow f(xi) = ei ei=yi−exp(axi2+bxi+c)⇒f(xi)=ei
待估计变量 a , b , c a,b,c a,b,c,注意这里的自变量不是 x x x不是向量 [ a , b , c ] [a,b,c] [a,b,c],这里的雅克比就是梯度
{ ∂ e i ∂ a = − x 2 ∗ e x p ( a x 2 + b x + c ) ∂ e i ∂ b = − x ∗ e x p ( a x 2 + b x + c ) ∂ e i ∂ c = − e x p ( a x 2 + b x + c ) \begin{cases} &\frac{\partial ei}{\partial a} = -x_{2}*exp(ax^{2}+bx+c) \\ &\frac{\partial ei}{\partial b} = -x*exp(ax^{2}+bx+c)\\ &\frac{\partial ei}{\partial c} = -exp(ax^{2}+bx+c) \end{cases} ⎩⎪⎨⎪⎧∂a∂ei=−x2∗exp(ax2+bx+c)∂b∂ei=−x∗exp(ax2+bx+c)∂c∂ei=−exp(ax2+bx+c)
J i = [ ∂ e i ∂ a ∂ e i ∂ b ∂ e i ∂ c ] J_{i}=\begin{bmatrix} \frac{\partial ei}{\partial a} &\frac{\partial ei}{\partial b} &\frac{\partial ei}{\partial c} \end{bmatrix} Ji=[∂a∂ei∂b∂ei∂c∂ei]
最终代入高斯牛顿的公式中
∑ J x i J x i T △ x = ∑ − e i ∗ J ( x i ) T ⇒ ∑ H i △ X = ∑ b i \sum J_{xi}J_{xi}^T \bigtriangleup x = \sum -ei*J_(xi)^T \Rightarrow \sum Hi \bigtriangleup X=\sum bi ∑JxiJxiT△x=∑−ei∗J(xi)T⇒∑Hi△X=∑bi
得到线性方程之后,即可每次求解,迭代更新,
△ X = H . l d l t ( ) . s o l v e ( b ) \bigtriangleup X = H.ldlt().solve(b) △X=H.ldlt().solve(b)
手写高斯牛顿
//
// Created by lyr on 2022/1/12.
//
#include "iostream"
#include ceres曲线拟合
整个就更简单了 ,只需要传入优化的参数,计算残差,计算整体的雅克比即可,重新实现一下Evaluate函数
//
// Created by lyr on 2022/1/12.
//
#include 自动求导,只需要知道残差也就是误差项跟优化变量,雅克比cere自动求出来
#include g2o曲线拟合
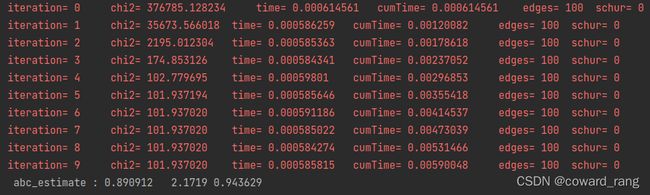
g2o曲线拟合跟上面的一样,知道待优化的变量,定义好残差就行,这里计算了雅克比
//
// Created by lyr on 2022/1/12.
//
#include 雅克比自己不计算,需要g2o自动计算的话,就不需要实现 l i n e a r i z e O p l u s linearizeOplus linearizeOplus
//
// Created by lyr on 2022/1/12.
//
#include (_vertices[0]);
// const Eigen::Vector3d abc = v->estimate();
// _jacobianOplusXi[0] = -_x * _x * exp(abc[0]*_x*_x +abc[1]*_x+abc[2]);
// _jacobianOplusXi[1] = -_x * exp(abc[0]*_x*_x +abc[1]*_x+abc[2]);
// _jacobianOplusXi[2] = -exp(abc[0]*_x*_x +abc[1]*_x+abc[2]);
// }
bool read(std::istream &is)override {
}
bool write(std::ostream &os) const override {
}
public:
double _x;
};
int main() {
double ar = 1.0, br = 2.0, cr = 1.0; //真实的参数值
double ae = 2.0, be = -1.0, ce = 5.0; //估计参数值
int N = 100; //数据点的个数
double w_sigma = 1.0; //噪声sigma值(标准差)
double inv_sigma = 1.0 / w_sigma;
cv::RNG rng; //opencv随机数产生器
/**
* 带有噪声的曲线:y = exp(ar*x^2 +br*x + cr) + w;//其中w是满足高斯分布的噪声w~(0,sigma^2)
* *****/
std::vector<double> x_data, y_data; //存储含有噪声的真实数据
for (int i = 0; i < N; i++) {
double x = i / 100.0;
x_data.push_back(x);
/**产生一个满足真实的曲线的方程 + 协方差为w_sigma^2的高斯分布的随机数***/
y_data.push_back(exp(ar * x * x + br * x + cr) + rng.gaussian(pow(w_sigma, 2)));
}
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3,1>>BlockSolverType; // 优化变量的维度是3维(ae,be,ce),误差项是1维
//线性求解器的类型
typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType>LinearSolverType;
//选择优化方法
auto solver = new g2o::OptimizationAlgorithmGaussNewton(g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
//创建图模型 设置优化方法
g2o::SparseOptimizer optimizer;
optimizer.setVerbose(true);
optimizer.setAlgorithm(solver);
//往图里面添加顶点(待优化的变量)
CurveFittingVertex *v = new CurveFittingVertex();
v->setEstimate(Eigen::Vector3d(ae,be,ce)); //这个就是传入一个预测值 (也就是给这个类里面的_estimate赋初值)
v->setId(0);
optimizer.addVertex(v); //加入到顶点
//往图中增加边(误差项)
for(int i = 0 ;i<N;i++)
{
CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]);
edge->setId(i);
edge->setVertex(0,v); //设置连接的顶点(只有一个顶点)
edge->setMeasurement(y_data[i]); // 观测数值
// 信息矩阵:协方差矩阵之逆(这里讲的是对加的误差项的一个置信度)
edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) );
optimizer.addEdge(edge);
}
optimizer.initializeOptimization();
optimizer.optimize(10); //迭代次数
Eigen::Vector3d abc_estimate = v->estimate(); //估计是顶点,这里只有一个定点,返回顶点的估计值
std::cout <<" abc_estimate : "<<abc_estimate.transpose()<<"\n";
return 0;
}
参考[1]: <视觉slam十四讲>