单链表输入和正序输出c语言,数据结构与算法——单链表及第三次实验题解

数据结构与算法——单链表及第三次实验题解

数据结构与算法——单链表及第三次实验题解

数据结构与算法——单链表及第三次实验题解

文章目录

数据结构与算法——单链表及第三次实验题解

学习思路

单链表的基本结构

单链表的基本操作

定义单链表——C++版

创建单链表

插入元素

在头部插入元素

在尾部插入元素

头指针与尾指针的区别

删除元素

遍历元素

求单链表的长度

单链表的进阶操作

输出单链表

销毁单链表

以已有数组为基础创建单链表

倒序创建——头插法

正序创建——尾插法

删除第i个元素

在第i个元素后插入值为value的结点

找到值为value的元素，并返回它的位置

题解

1:整数单链表的基本运算-1

描述

输入

输出

样例输入

样例输出

题解1

2:整数单链表的基本运算-2

描述

输入

输出

样例输入

样例输出

题解2

3:单链表的插入和显示操作

描述

输入

输出

样例输入

样例输出

题解3

这块涉及很多指针，所以对很多同学来说都会有难度。我觉的应该先抓一些基本操作，然后再去看大的算法设计是由哪些基本操作构成的。基本操作大概包括：

创建单链表；

插入元素；

删除元素；

遍历单链表；

书上的结构体、动态内存分配都是用C语言的结构体实现的，但我觉得大家可能对C++的new和delete更熟悉一点，而且C++的结构体形式也更加简单，所以后续的代码都将用C++给出

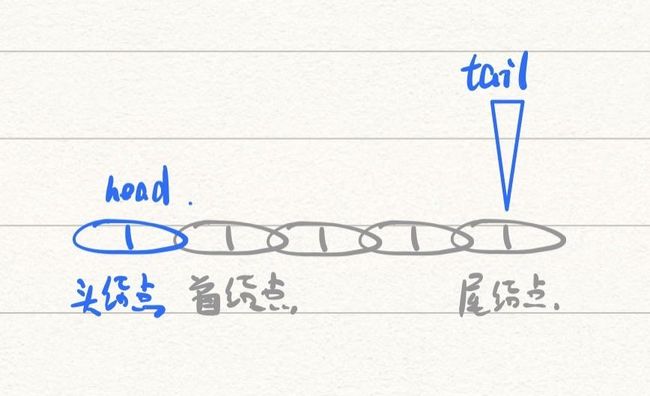
单链表是由一个个的结点组成，每个节点都是指针类型的变量，都包含数据域和指针域。其中数据域用来存储数据，指针域用来连接下一个结点：

我们用来存储数据的单链表是由一个个上面这样的结点组成的，对于每个节点，你可以通过它找到它下一个结点，但你不可以通过它找到它上一个结点，这就决定了要对单链表进行操作，必须找到目标结点的上一个结点

为了便于操作，我们经常给单链表添加头指针和尾指针，分别指向首结点和尾结点

定义单链表——C++版

struct node{

int data; //数据域

node *next; //指针域

};

创建单链表

与创建数组不同，最初创建单链表，其实就是创建头指针，后续的“扩大单链表”，其实就是给头指针上挂上其他的链条。

所以我建议大家直接将“创建单链表”理解为“创建头指针”，然后将其他的赋值、完善等操作理解为“给头指针挂上新的链条”。

创建头指针用到如下代码

node *head;

head=new node();

head->next=NULL;

方便起见，我们把后两句存放在一个初始化函数里：

void initList(node *&head){ //初始化函数

head=new node();

head->next=NULL;

}

这样以后创建头指针的时候，只要写：

node *head;

initList(head);

就可以创建好了。

插入元素

插入元素可以很形象地理解为在一条链子上插入新的一环。比如将结点p插入到两个结点之间，也就是插入到结点before之后，其实是这样的过程：

p->next=before->next; //p的指针域连接last后面的环

before->next=p; //last的指针域连接p

在头部插入元素

如果我要在最头上插入一个新结点，那我找不到before，怎么办？

这就体现出头指针head的作用了，头指针head的存在保证了就算你想在最开始的位置插入结点，你还是能找到一个before，来完成你的操作。

p->next=head->next; //p的指针域指向原来的首结点

head->next=p; //头指针指向p，p成为新的首结点

在尾部插入元素

在尾部插入元素时，最后的元素相当于before，但没有before->next。我们在最后加一个尾指针tail，这样插入元素时，情况又变成了在两个“结点”之间插入一个新的结点。

但值得注意的是，尾指针指向最后一个元素，而不是最后一个元素指向尾指针，所以插入操作与前面略有不同：

tail->next=p; //tail->next表示尾结点的指针域

tail=p; //尾指针指向新的尾结点p

头指针与尾指针的区别

需要注意的是，头指针其实是头结点的指针域，也就是说，头指针本身是一个结点，但尾指针并不是结点，它只是一个单纯的指针。

头指针通过指针域来发挥“指针”的作用，也就是说，首结点是head->next。在实际应用中，我们要输出首结点的数据，其实是这样输出的：

coutdata;

而尾指针就是一个纯粹的指针，尾结点就是tail，所以如果要输出尾结点的数据，是这样的：

cout

在初始化单链表，也就是创建头指针的过程中，如果需要添加尾指针，应该是这样的：

void initList_tail(node *&head){

head=new node();

head->next=NULL;

node *tail=head;

}

因为刚创建头指针的过程中，头指针本身就是最后一个元素，所以按照尾指针的定义，应该让尾指针指向最后一个元素，也就是指向头指针。

删除元素

删除元素也可以类比取下链条中的某一环，并把这一环销毁。思路应该是创建一个临时指针，用来代表这个即将被销毁的结点，然后重新连接链条，并销毁待删除的结点。

node *q=before->next;

before->next=q->next;

delete q;

遍历元素

单链表的遍历特别有顺藤摸瓜捣毁黑帮的感觉，就像你手里掌握着黑帮老大——头指针，然后通过他，你能找到他的小弟，然后找到小弟的小弟…最后找到的那个人，他是黑帮最底层的人，他没有小弟——NULL。

需要注意的有两点：

黑帮成员之间有鲜明的等级观念，只有上级能联系下属，下属无法联系上级，也就是说单链表的遍历是单向的

黑帮老大是个重要人物，不能出事，因为我们一旦失去了黑帮老大，就再也控制不住整个黑帮了。所以每次遍历的时候，我们需要额外找个跑腿的——工作指针p，用它来联系小弟们，以保证老大head不被改变。

综上，遍历的操作应该是：

void findBro(node *head){

node *p=head; //工作指针

//或：node *p=head->next;

while(p!=NULL){ //判断当前的人是不是最底层小弟

//操作

p=p->next; //找他的小弟

}

}

求单链表的长度

掌握了遍历的方法后，我们可以在遍历过程中夹带一点私货，比如记录一下这个黑帮一共有多少人——求单链表长度：

int getLength(node *head){ //求长度

int count=0;

node *p=head->next; //工作指针

while(p!=NULL){

p=p->next;

count++;

}

return count;

}

有了count的引入，就为我们的操作带来了更多的可能，比如判断if(count==i)，以实现找到第i个元素等，在后面的部分会给出相应的代码

输出单链表

void output(node *head){ //其实就是在遍历过程中加一个输出

node *p=head->next;

while(p!=NULL){

cout

p=p->next;

}

cout<

}

销毁单链表

拆分为基本操作：遍历+单个元素删除

void destoryList(node *&head){ //销毁

node *pre=head,*p=head->next; //从头结点开始删除

while(p!=NULL){

delete pre;

pre=p;

p=p->next;

}

}

以已有数组为基础创建单链表

倒序创建——头插法

拆分为基本操作：不断地往表头插入新结点

void createList(node *&head,int a[],int len){ //已有数组a，数组长度len

for(int i=0;i

node *s=new node(); //创建一个游离的新结点

s->data=a[i]; //给新结点赋值

s->next=head->next; //把新结点插入链表的前端

head->next=s;

}

}

正序创建——尾插法

拆分为基本操作：不断地往表尾插入新的结点

void createList_tail(node *head,int a[],int len){

node *tail=head;

for(int i=0;i

node *s=new node(); //创建一个游离的新结点

s->data=a[i]; //给新结点赋值

tail->next=s; //把新结点插入链表的尾端

tail=s;

}

}

删除第i个元素

拆分为基本操作：遍历到第i-1个元素的位置，删除它后面的元素

void deleElem(node *&head,int i){ //删除第i个元素

node *p=head; //工作指针

int count=1;

while(p!=NULL&&count!=i){

p=p->next;

count++;

}

node *q=p->next; //基本操作——删除

p->next=q->next;

delete q;

}

在第i个元素后插入值为value的结点

拆分为基本操作：遍历到第i个元素的位置，在它后面插入新的元素

void insElem(node *&head,int value,int i){ //在第i个元素后插入值为value的结点

node *p=head->next; //工作指针

int count=1;

while(p!=NULL&&count!=i){

p=p->next;

count++;

}

node *q=new node(); //创建

q->data=value;

q->next=p->next;

p->next=q;

}

ps. i=0时在头结点后直接插入结点

找到值为value的元素，并返回它的位置

拆分为基本操作：遍历单链表直到找到value，然后输出此时的count

int findValue(node *head,int value){

node *p=head->next;

int count=1;

while(p!=NULL&&p->data!=value)

{

p=p->next;

count++;

}

return count;

}

1:整数单链表的基本运算-1

题目链接：传送门

描述

设计整数单链表的基本运算程序，并用相关数据进行测试

输入

顺序输入单链表A的各个元素

输出

第一行：创建单链表A后，输出所有元素

第二行：删除第一个元素，输出删除后的所有元素

第三行：输出删除元素后表的长度

第四行：在第二元素处插入一个新的元素100

第五行：输出第一个元素100所在位置

样例输入

1 2 3 4 0 9

样例输出

1 2 3 4 0 9

2 3 4 0 9

5

2 100 3 4 0 9

2

题解1

#include

using namespace std;

struct node{ //定义链表

int data;

node *next;

};

//头结点用head表示

void initList(node *&head){ //初始化函数

head=new node();

head->next=NULL;

}

void destoryList(node *&head){ //销毁链表

node *pre=head,*p=head->next; //从头结点开始删除

while(p!=NULL){

delete pre;

pre=p;

p=p->next;

}

}

int getLength(node *head){ //求长度

int count=0;

node *p=head->next;

while(p!=NULL){

p=p->next;

count++;

}

return count;

}

int findValue(node *head,int value){ //找到值为value的结点

node *p=head->next;

int count=1;

while(p!=NULL&&p->data!=value)

{

p=p->next;

count++;

}

return count;

}

void insElem(node *&head,int value,int i){ //在第i个元素后插入值为value的结点

node *p=head->next;

int count=1;

while(p!=NULL&&count!=i){

p=p->next;

count++;

}

node *q=new node();

q->data=value;

q->next=p->next;

p->next=q;

}

void deleElem(node *&head,int i){ //删除第i个元素

node *p=head;

int count=1;

while(p!=NULL&&count!=i){

p=p->next;

count++;

}

node *q=p->next;

p->next=q->next;

delete q;

}

void output(node *head){ //输出

node *p=head->next;

while(p!=NULL){

cout

p=p->next;

}

cout<

}

void createList_tail(node *head,int a[],int len){ //尾插法创建链表

node *tc=head;

for(int i=0;i

node *s=new node();

s->data=a[i];

tc->next=s;

tc=s;

}

}

int main()

{

node *head;

initList(head);

int a[10000];

for(int i=0;i<6;i++)cin>>a[i];

createList_tail(head,a,6);

output(head);

deleElem(head,1);

output(head);

cout<

insElem(head,100,1);

output(head);

cout<

destoryList(head);

return 0;

}

2:整数单链表的基本运算-2

题目链接：传送门

描述

设计有序整数单链表的插入运算程序，并用相关数据进行测试

输入

按升序顺序输入单链表A的各个元素和待插入元素

输出

第一行：创建单链表A后，输出所有元素

第二行：输出按照升序插入后的所有元素

样例输入

0 1 2 3 4 9

7

样例输出

0 1 2 3 4 9

0 1 2 3 4 7 9

题解2

这个题需要稍微拐一个弯，就是需要找到插入位之前的元素，所以在比较大小的过程中，需要把手伸的长一点，即如果下一个元素的数值大于待插入元素，那么工作指针p停留在当前元素：

#include

using namespace std;

struct node{

int data;

node *next;

};

//头结点用head表示

void initList(node *&head){ //无值初始化

head=new node();

head->next=NULL;

}

void destoryList(node *&head){ //销毁

node *pre=head,*p=head->next; //从头结点开始删除

while(p!=NULL){

delete pre;

pre=p;

p=p->next;

}

}

void output(node *head){

node *p=head->next;

while(p!=NULL){

cout

p=p->next;

}

cout<

}

void createList_tail(node *head,int a[],int len){

node *tc=head;

for(int i=0;i

node *s=new node();

s->data=a[i];

tc->next=s;

tc=s;

}

}

int main()

{

node *head;

initList(head);

int a[1000],value;

for(int i=0;i<6;i++)cin>>a[i];

cin>>value;

createList_tail(head,a,6);

output(head);

node *p=head->next;

while(p!=NULL&&p->next->data<=value)

p=p->next;

node *s=new node();

s->data=value;

s->next=p->next;

p->next=s;

output(head);

destoryList(head);

return 0;

}

3:单链表的插入和显示操作

题目链接：传送门

描述

使用尾插法创建链表，查找链表值最大结点(假定当前链表最大值唯一)，在最大值结点后插入一个比最大值大10的结点。

#include

#include

using namespace std;

typedef int ElemType;

#define MAX_SIZE 100

typedef struct node

{

ElemType data;//数据域

struct node *next;//指针域

} SLinkNode;//单链表结点类型

void CreateListR(SLinkNode *&L, ElemType a[], int n)//尾插法建表

{

SLinkNode *s, *tc; int i;

L = (SLinkNode *)malloc(sizeof(SLinkNode));//创建头结点

tc = L;//tc为L的尾结点指针

for (i = 0; i < n; i++)

{

s = (SLinkNode *)malloc(sizeof(SLinkNode));

s->data = a[i];//创建存放a[i]元素的新结点s

tc->next = s;//将s结点插入tc结点之后

tc = s;

}

tc->next = NULL;//尾结点next域置为NULL

}

int InsElemSpe(SLinkNode *&L)//插入结点

{

// 在此处补充你的代码

return 1;//插入运算成功,返回1

}

void DispList(SLinkNode *L)//输出单链表

{

SLinkNode *p = L->next;

while (p != NULL)

{

cout

p = p->next;

}

cout<

}

void DestroyList(SLinkNode *&L)//销毁单链表L

{

SLinkNode *pre = L, *p = pre->next;

while (p != NULL)

{

free(pre);

pre = p; p = p->next;//pre、p同步后移

}

free(pre);

}

int main()

{

ElemType a[MAX_SIZE];

SLinkNode *L;

int nlength;

cin >> nlength;

for (int i = 0; i < nlength; i++)

cin >> a[i];

CreateListR(L, a, nlength);

InsElemSpe(L);

DispList(L);

DestroyList(L);

return 0;

}

输入

输入分两行数据，第一行是尾插法需要插入的数据的个数，第二行是具体插入的数值。

输出

按程序要求输出

样例输入

4

40 50 70 65

样例输出

40 50 70 80 65

题解3

只给出自己写的那部分函数：

int InsElemSpe(SLinkNode *&L)

{

// 在此处补充你的代码

SLinkNode *p=L->next;

int max_value=0;

while (p!=NULL){

max_value=max(max_value,p->data);

p=p->next;

}

SLinkNode *pp=L->next;

while(pp!=NULL&&pp->data!=max_value)

pp=pp->next;

SLinkNode *q=(SLinkNode*)malloc(sizeof(SLinkNode));

q->data=max_value+10;

q->next=pp->next;

pp->next=q;

return 1;//插入运算成功,返回1

}

数据结构与算法——单链表及第三次实验题解相关教程

数据结构详解系列第一章 绪论

数据结构详解系列：第一章 绪论 本章主要需要了解数据结构中的一些基本概念，区别逻辑结构和物理结构。 文章目录 前言 总览： ①基本概念和术语 总览： ①基本概念和术语 数据： ? 能够描述客观事物属性，且能够输入到计算机中 被识别和处理的符号集合 。 数

高阶数据结构之AVL树

高阶数据结构之AVL树 AVL树的插入实现 AVL树是二叉平衡树，即在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。 二叉搜索树 特征： 任取树中的结点，要求结点的左子树中的所有key全部小于结点的key 结点的右子树中的所有key全部大于

数据结构详解系列：第二章 线性表

数据结构详解系列：第二章 线性表 前言 本章主要详解了线性表(逻辑结构)对应的顺序表和链表(存储结构)的实现方式，其中包含增删改查的操作的多种实现方法及代码，最后还介绍了一些特殊链表的引入，以解决现有的存储结构存在的一些问题缺陷。 文章目录 前

最短路径算法

最短路径算法 为什么80%的码农都做不了架构师？ 问题描述：给你一个顶点做源点，你想要知道，如何从源点到达其他所有点的最短路径。 OK，这个问题看起来没什么用。我们一般想知道的是A点到B点的最短路径，这个单源最短路径问题告诉我们A点到所有点的最短路径

【算法系列 四】 String

【算法系列 四】 String 为什么80%的码农都做不了架构师？ 1. 字符串循环左移(九度OJ1362)，要求时间复杂度O(N)，空间复杂度O(1) 这是一道基本的题目，简单说来就是三次翻转 比如：abcdef 左移两位 cdefab 过程： ab 翻转 ba cdef 翻转 fedc 将上面两个翻转后

从代码出发：多层全连接神经网络反向传播算法代码剖析

从代码出发：多层全连接神经网络反向传播算法代码剖析 BP反向传播算法剖析 代码 运行过程 最后结果可视化 数据分布 最后结果 ‘’’ 写在前面： 复习了一边BP算法，照着书上代码研究了一遍，加了些注释。代码看起来还能接受，自己照着写出来的就出现各种问题

数据结构详解系列：第三章 栈和队列

数据结构详解系列：第三章 栈和队列 前言 本章主要详解了栈和队列以及特殊矩阵的压缩知识，其中包括栈的顺序存储和链式存储，队列的顺序存储以及链式存储，循环队列的顺序实现以及优化改进-双端队列，最后介绍了三种特殊矩阵的存储结构压缩算法。 文章目录 前

优秀数据结构学习 - 共享内存无锁队列的实现(二)

优秀数据结构学习 - 共享内存无锁队列的实现(二) 1 关键技术 操作系统提供的进程间通信机制有文件、socket、消息队列、管道、共享内存等。其中，共享内存是最快的IPC机制[6]。 共享内存映射到进程空间后，数据可以直接从共享内存进行读写，不需要执行系统调