np.meshgrid()函数
文章目录
-
- (1)自己理解
- (2)官方解释
- (3)参数:
-
- 3.1 x1, x2,…, xn:array_like
- 3.2 sparse:bool, optional 默认false
- 3.3 copy:bool, optional
(1)自己理解
np.meshgrid(a, b,indexing = "xy") 函数会返回 b.shape() 行 ,a.shape() 列的二维数组。
因此 i, j 都是 b.shape()行 a.shape() 列 的二维数组。
(2)官方解释
参考:https://numpy.org/doc/stable/reference/generated/numpy.meshgrid.html
代码:numpy.meshgrid(*xi, copy=True, sparse=False, indexing='xy')
作用:给定一维坐标数组 x1、x2、…、xn,制作 N 维坐标数组以对 N 维网格上的 N 维标量/矢量场进行矢量化评估。
(3)参数:
3.1 x1, x2,…, xn:array_like
表示网格坐标的一维数组。
indexing:{'xy', 'ij'}, optional
可选参数,用于设置输出的是笛卡尔(‘xy’,默认)还是矩阵(‘ij’)索引。此函数通过索引关键字参数支持两种索引约定。
给出字符串“ij”返回一个带有矩阵索引的网格,而“xy”返回一个带有笛卡尔索引的网格。
在输入长度为 M 和 N 的二维情况下,对于“xy”索引,输出形状为 (N, M),对于“ij”索引,输出形状为 (M, N)。
在输入长度为 M、N 和 P 的 3-D 情况下,对于“xy”索引,输出的形状为 (N, M, P),对于“ij”索引,输出的形状为 (M, N, P)。
简单示例 (python代码)
import numpy as np
x = [1, 2, 3, 4]
y = [7, 8, 9]
X, Y = np.meshgrid(x, y)
print("X:")
print(X)
print("Y:")
print(Y)
print("==============================")
X1, Y1 = np.meshgrid(x, y,indexing='xy')
print("X1:")
print(X1)
print("Y1:")
print(Y1)
print("==============================")
X2, Y2 = np.meshgrid(x, y,indexing='ij')
print("X2:")
print(X2)
print("Y2:")
print(Y2)
结果输出:
X:
[[1 2 3 4]
[1 2 3 4]
[1 2 3 4]]
Y:
[[7 7 7 7]
[8 8 8 8]
[9 9 9 9]]
==============================
X1:
[[1 2 3 4]
[1 2 3 4]
[1 2 3 4]]
Y1:
[[7 7 7 7]
[8 8 8 8]
[9 9 9 9]]
==============================
X2:
[[1 1 1]
[2 2 2]
[3 3 3]
[4 4 4]]
Y2:
[[7 8 9]
[7 8 9]
[7 8 9]
[7 8 9]]
3.2 sparse:bool, optional 默认false
简单示例 (注:为True的看上面示例)
import numpy as np
x = [1, 2, 3, 4]
y = [7, 8, 9]
X, Y = np.meshgrid(x, y,sparse=True)
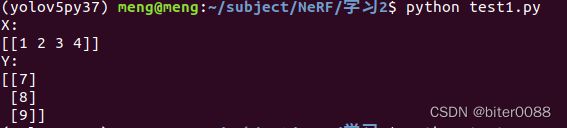
print("X:")
print(X)
print("Y:")
print(Y)
结果输出:
X:
[[1 2 3 4]]
Y:
[[7]
[8]
[9]]
meshgrid 对于评估网格上的函数非常有用。如果函数依赖所有坐标,可以使用参数 sparse=True 来节省内存和计算时间。
简单示例:
import numpy as np
x = [1, 2, 3, 4]
y = [7, 8, 9]
X, Y = np.meshgrid(x, y,sparse=True)
zs = np.sqrt(X**2 + Y **2)
print("X.shape,Y.shape,zs.shape",X.shape,Y.shape,zs.shape)
print("==============================")
X1, Y1 = np.meshgrid(x, y,sparse=False)
zz = np.sqrt(X1**2 + Y1 **2)
print("X1.shape,Y1.shape,zz.shape",X1.shape,Y1.shape,zz.shape)
print("==============================")
print(np.array_equal(zz, zs))
结果输出:
X.shape,Y.shape,zs.shape (1, 4) (3, 1) (3, 4)
==============================
X1.shape,Y1.shape,zz.shape (3, 4) (3, 4) (3, 4)
==============================
True