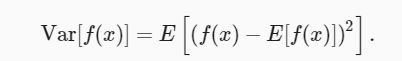动手学深度学习 ——概率论基础

基本概率论

假设我们掷骰子，想知道看到1的几率有多大，而不是看到另一个数字。 如果骰子是公平的，那么所有六个结果 {1,…,6} 都有相同的可能发生， 因此我们可以说 1 发生的概率为 1/6 。

然而现实生活中，对于我们从工厂收到的真实骰子，我们需要检查它是否有瑕疵。 检查骰子的唯一方法是多次投掷并记录结果。 对于每个骰子，我们将观察到 {1,…,6} 中的一个值。 对于每个值，一种自然的方法是将它出现的次数除以投掷的总次数， 即此事件（event）概率的估计值。 大数定律（law of large numbers）告诉我们： 随着投掷次数的增加，这个估计值会越来越接近真实的潜在概率。
在统计学中，我们把从概率分布中抽取样本的过程称为抽样（sampling）。 笼统来说，可以把分布（distribution）看作是对事件的概率分配。 将概率分配给一些离散选择的分布称为多项分布（multinomial distribution）。

概率论公理

在处理骰子掷出时，我们将集合 S={1,2,3,4,5,6} 称为样本空间（sample space）或结果空间（outcome space）， 其中每个元素都是结果（outcome）。 事件（event）是一组给定样本空间的随机结果。 例如，“看到 5 ”（ {5} ）和“看到奇数”（ {1,3,5} ）都是掷出骰子的有效事件。 注意，如果一个随机实验的结果在 A 中，则事件 A 已经发生。 也就是说，如果投掷出 3 点，因为 3∈{1,3,5} ，我们可以说，“看到奇数”的事件发生了。
概率（probability）可以被认为是将集合映射到真实值的函数。 在给定的样本空间 S 中，事件 A 的概率， 表示为 P(A) ，满足以下属性:

• 对于任意事件 A ，其概率从不会是负数，即 P(A)≥0 ；
• 整个样本空间的概率为 1 ，即 P(S)=1 ；
• 对于互斥（mutually exclusive）事件（对于所有 i≠j 都有 Ai∩Aj=∅ ）的任意一个可数序列 A1,A2,… ，序列中任意一个事件发生的概率等于它们各自发生的概率之和，即 P(⋃∞i=1Ai)=∑∞i=1P(Ai) 。

有了这个公理系统，我们可以避免任何关于随机性的哲学争论； 相反，我们可以用数学语言严格地推理

随机变量

在我们掷骰子的随机实验中，我们引入了随机变量（random variable）的概念。 随机变量几乎可以是任何数量，并且它可以在随机实验的一组可能性中取一个值。

联合概率

第一个被称为联合概率（joint probability） P(A=a,B=b) 。 给定任意值 a 和 b ，联合概率可以回答： A=a 和 B=b 同时满足的概率是多少？ 请注意，对于任何 a 和 b 的取值， P(A=a,B=b)≤P(A=a) 。 这点是确定的，因为要同时发生 A=a 和 B=b ， A=a 就必须发生， B=b 也必须发生（反之亦然）。因此， A=a 和 B=b 同时发生的可能性不大于 A=a 或是 B=b 单独发生的可能性。

条件概率

联合概率的不等式带给我们一个有趣的比率： 0≤P(A=a,B=b)/P(A=a)≤1 。 我们称这个比率为 条件概率（conditional probability）， 并用 P(B=b∣A=a) 表示它：它是 B=b 的概率，前提是 A=a 已发生。

贝叶斯定理

使用条件概率的定义，我们可以得出统计学中最有用的方程之一：Bayes定理（Bayes’ theorem）。 根据乘法法则（multiplication rule ）可得到 P(A,B)=P(B∣A)P(A) 。 根据对称性，可得到 P(A,B)=P(A∣B)P(B) 。 假设 P(B)>0 ，求解其中一个条件变量，我们得到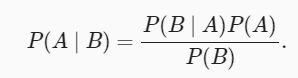
其中 P(A,B) 是一个联合分布（joint distribution）， P(A∣B) 是一个条件分布（conditional distribution）。 这种分布可以在给定值 A=a,B=b 上进行求值。

边际化

为了能进行事件概率求和，我们需要求和法则（sum rule）， 即 B 的概率相当于计算 A 的所有可能选择，并将所有选择的联合概率聚合在一起：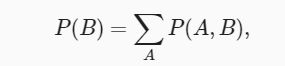
这也称为边际化（marginalization）。 边际化结果的概率或分布称为边际概率（marginal probability） 或边际分布（marginal distribution）。

独立性

依赖（dependence）与独立（independence）。 如果两个随机变量 A 和 B 是独立的，意味着事件 A 的发生跟 B 事件的发生无关。 在这种情况下，统计学家通常将这一点表述为 A⊥B 。 根据贝叶斯定理，马上就能同样得到 P(A∣B)=P(A) 。 在所有其他情况下，我们称 A 和 B 依赖。 比如，两次连续抛出一个骰子的事件是相互独立的。
由于 P(A∣B)=P(A,B)/P(B)=P(A) 等价于 P(A,B)=P(A)P(B) ， 因此两个随机变量是独立的，当且仅当两个随机变量的联合分布是其各自分布的乘积。 同样地，给定另一个随机变量 C 时，两个随机变量 A 和 B 是条件独立的（conditionally independent）， 当且仅当 P(A,B∣C)=P(A∣C)P(B∣C) 。 这个情况表示为 A⊥B∣C 。

期望和方差

为了概括概率分布的关键特征，我们需要一些测量方法。 一个随机变量 X 的期望（expectation，或平均值（average））表示为

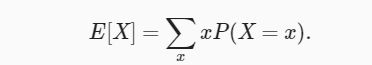
当函数 f(x) 的输入是从分布 P 中抽取的随机变量时， f(x) 的期望值为

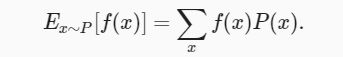
衡量随机变量 X 与其期望值的偏置。这可以通过方差来量化

方差的平方根被称为标准差（standard deviation） 随机变量函数的方差衡量的是：当从该随机变量分布中采样不同值 x 时， 函数值偏离该函数的期望的程度：