Polarized 3D翻译

Polarized 3D阅读

Polarized 3D: High-Quality Depth Sensing with Polarization Cues 偏振三维:高质量的偏振线索深度感知

Abstract

​ 为解决偏振法线进行深度增强中物理的伪影的影响，比如方位模糊、折射失真和前端并行信号退化。提出了一种将偏振的表面法线(polarization normals)与对齐的深度图相结合的框架来增强粗深度图。

1. Introduction

​ 如今，消费类3D相机制作的深度地图往往很嘈杂，而且缺乏足够的细节。因此，增强从Kinect等紧凑传感器获得的3D深度地图是一个越来越受欢迎的研究领域。其中一个最有前途的解决方案是将捕获的粗糙深度地图与从立体光度(PS-photometric stereo)或阴影形状(SfS-shape-from-shading)获得的表面法线相结合。这种深度法向融合是有逻辑的——粗深度图提供几何结构，表面法线捕捉待融合的细节。将低质量的深度图与SfS或PS获得的表面法线图结合在一起的论文有几十篇。比较受欢迎的论文包括使用SfS的[44,14,43]和使用PS的[31,15]。作为一种补充技术，我们建议首先使用极化的表面法线来增强深度图。

​ 物体的形状会对反射光的偏振产生微小的变化，旋转数码相机前的偏振滤光片就可以得到最好的效果。通过偏振获得表面法线比SfS和PS有潜在的优势，包括:

• 被动Passive捕获:假设入射到物体上的光是非偏振的，可以通过旋转成像传感器上的偏振器来获得表面法线。
• 对漫反射(diffuse interreflections)的鲁棒性:与SfS和PS不同，漫反射不会显著破坏估计的形状。
• 材料不变捕获:从偏振光问题的形状物理适用于从电绝缘到金属到半透明物体的材料。
• 照明鲁棒捕获:如果入射光是非偏振的，则形状估计是可靠的，并且可以在室内，室外或在有图案的照明下进行。

然而，利用偏振光法获得表面法线的方法尚不成熟。得到的法线被剧烈地扭曲了。具体的未决问题[24,3]包括:

1. 模糊度：表面法线的方位角分量包含了π弧度的模糊度，这导致三维形状的模糊翻转。
2. 折射率失真：获得表面法线的天顶分量需要折射率的知识来估计精确的三维形状。
3. 平行于正面的表面：当天顶角接近零时，获得的法线是有噪声的。
4. 深度不连续：即使法线得到正确，也必须进行梯度积分以恢复3D形状。
5. 相对深度：积分表面法线只能得到相对的三维形状，直到偏移量和缩放常数。

​ 在这篇论文中，我们解决了这些挑战的每一个，通过一个粗糙的深度图开始，作为一个约束，以纠正从偏振光获得的法线。虽然我们不能解决所有的开放问题，但我们的校正足以使用偏振法线来增强深度图。图1中概述了我们的方法

图1所示。建议的技术大纲。(a)一个物体的Kinect深度与(b)三张偏光滤镜不同旋转的照片相结合。©从菲涅耳方程(Fresnel equations)得到曲面法线的积分。注意方位模糊（azimuthal ambiguity）（视作一个形状的翻转）和天顶角（zenith angle）的扭曲（视作形状的平整度）。(d)对方位模糊校正后的曲面法线积分消除了翻转，对天顶失真校正后，采用基于物理的积分，最终结果如(e)所示。

1.1. Contributions

​ 从概念上讲，我们提出了利用偏振线索的法线来提高粗深度图质量的唯一技术。我们设计了一个基于物理的框架，其中粗深度图用于解决方位模糊（解决问题1）和修正折射失真（解决问题2），为了恢复三维形状，我们提出了一种==以偏振度作为加权参数的生成树积分方案。这种方法是专为偏振光法线设计的，解决了问题3。==众所周知，深度和法线的一般融合可以解决问题4和问题5。

2. Related Work

偏光形状Shape from Polarization (SfP)：通过分析反射光的偏振特性来估计表面法线。在[36]中可以找到概述，它描述了如何使用镜面反射的偏振度和方向来获得表面法线。镜面偏振光中的信息也可以扩展到透明物体（transparent objects）[37,25]。另一方面，也可以利用漫射偏振反射来估计绝缘物体（dielectric objects）的形状[27,3]。综上所述，这些论文说明了在可控的研究环境下偏振光的好处，但是，不管使用哪种偏振光技术，SfP 线索仍然是一个不适定的问题，因为形状上有一些模糊之处。这包括，例如，在求解估算的表面法线的方位角和天顶分量时缺乏一致性。为了解决这种模棱的问题，[2]使用两个视点来获得偏振测量。而[27]的工作则选择使用表面法线分布的先验，并在多视图数据[26]上扩展到空间雕刻获得粗糙形状。相比之下，我们使用额外的粗深度测量来充分解决经典SfP中的主要工件。

Combining depth and normal cues结合深度和法线线索：是目前一种流行的获取3D信息的技术。一般来说，现有技术结合了以几何为基础的技术来获得粗糙深度和以光度为基础的技术来获得表面法线。这种融合是很有动力的:（1）几何方法有助于消除光度测量技术中的模糊性，如SfS或未经校准的PS;（2）采用光度法将几何数据的表面细节添加到粗深度图中;（3）粗糙深度图为梯度曲面问题提供了锚点anchor，解决了深度不连续处的不可积曲面的挑战。现存的许多作品都部分或完全地反映了这三个方面。以前探索过的组合包括:激光扫描与PS[31]结合，多视角立体与SfS[42]或PS结合[47,19,7]，消费者深度感知与SfS结合[44,14,43]，消费者深度感知与PS结合[48,15,40]。如果无法获得高质量的表面法线，那么融合一系列重叠的深度图是一种流行的方法，可以为各种交互应用程序[17]或大规模实时表面重建[32]生成光滑表面。表1总结了我们提出的方法的优点和局限性。

表1。偏振允许在复杂的场景中增强深度，包括闪亮的物体、交互反射和不受控制的照明。单次拍摄是可能使用偏振相机。这些相机出售时带有用于多个偏振通道的传感器镶嵌图。

**Polarization in computational imaging计算成像中的偏振光:**一些研究人员已经利用偏光球面梯度照明图案和相机前的偏光镜来捕获偏光传输的行为，以进行静态表情的高分辨率面部扫描[22]，镜面粗糙度和各向异性的估计[9]，推论。 通过圆偏振提示[10，12]设置每个像素的表面反射率参数，以及进行多视图面部性能捕获[11]。偏振线索也广泛应用于计算成像应用，如漫反射和镜面反射的分离[30,49]、图像去雾[38]、图像拼接和全景拼接[39]、光照复用[6]和相机[23,18]或显示硬件[21]。此外，偏振线索还可以用于恢复半透明物体形状[5]、海面形状[46]或水下散射[41]。

3. Basics of shape from polarization

3.1. Surface normals from polarization cues

​ 照片是用偏光镜在一定角度${\varphi }_{\text{pol }}$拍摄的，在单个图像点上，强度intensity可以写成

$$I\left({\varphi }_{\mathrm{p}\mathrm{o}\mathrm{l}}\right)=\frac{I_{\mathrm{m}\mathrm{a}\mathrm{x}}+I_{\min }}{2}+\frac{I_{\max }-I_{\min }}{2}\cos \left(2\left({\varphi }_{\mathrm{p}\mathrm{o}\mathrm{l}}-\phi \right)\right)\text{\hspace{1em}(1)}$$

其中，方程中的三个未知变量为$I_{\mathrm{m}\mathrm{a}\mathrm{x}}$、$I_{\mathrm{m}\mathrm{i}\mathrm{n}}$和$\phi$，如图2所示。在正弦波上采样不同的值相当于用偏振镜角度的不同旋转来拍摄照片

图2。捕捉的设置。在(a)中，使用带有偏振滤光镜的标准相机在不同滤光镜旋转下拍摄扩散球体。下面一行捕捉到的照片看起来类似，但在(b)中，当一个像素与滤光片角度相对应时，观察到一个正弦模式。相位编码方位角，振幅和偏移编码天顶角。

Obtaining the azimuth of surface normal得到表面法线方位角：通过对${\varphi }_{\text{pol }}$的三个值进行采样，足以表征接收信号的幅度，相位和偏移，其中方位角$\phi$被编码为接收信号的相位。然而，需要注意的是，这个解决方案并不是唯一的：==在偏振图像中，通过π弧度分开的两个方位角是无法分辨的。==具体来说，其中$\phi$和$\phi$ + π的方位角对于等式1返回相同的值。在实践中，当使用偏振形状时，这将导致令人失望的结果。解决这种歧义是本文研究的重点之一。

Obtaining the zenith of surface normal得到表面法向顶点：偏振光程度由式1的振幅和偏移量决定，可表示为
$$\rho =\frac{I_{\max }-I_{\min }}{I_{\max }+I_{\min }}\text{\hspace{1em}(2)}$$
将菲涅耳Fresnel 方程(见[16])代入方程2，偏振度可以写成
$$\rho =\frac{{\left(n-\frac{1}{n}\right)}^2{\sin }^2\theta }{2+2n^2-{\left(n+\frac{1}{n}\right)}^2{\sin }^2\theta +4\cos \theta \sqrt{n^2-{\sin }^2\theta }}\text{\hspace{1em}(3)}$$

其中n为折射率，θ为天顶角。假设折射率已知，可以用封闭形式估计天顶角，也可以通过数值优化来估计。

Specular vs diffuse polarization镜面偏振与漫反射偏振：公==式3对于绝缘表面是稳健的，但不能用于非绝缘表面，如镜子或金属。这些材料不反射任何漫射光，==而是关系
$${\rho }^{\mathrm{s}\mathrm{p}\mathrm{e}\mathrm{c}}=\frac{2n\tan \theta \sin \theta }{{\tan }^2\theta {\sin }^2\theta +{\left|n^{\ast }\right|}^2}\text{\hspace{1em}(4)}$$
其中${\left|n^{\ast }\right|}^2=n^2\left(1+{\kappa }^2\right)$，κ是材料的衰减指数，可以求出天顶角[28]。可以确定是使用公式3还是4来获得基于单个像素偏振度的天顶角。这样描述的方法的变体是在以前的SfP工作中实施，由于SfP的局限性(参见第1节的要点1-5)，SfP从来没有被认为是SfS的可靠替代品。

4. Framework for Depth-Polarization Fusion

​ 假设场景具有以下属性:(1)非偏振环境光;(2)镜面无相互反射;(3)只有绝缘材料或低频材料发生变化;(4)漫反射主导曲面或镜面反射主导曲面

关于假设的细节，请参阅附录。

4.1. Correcting normals from polarization

​ 我们利用获得的深度图来纠正偏振光法向的系统畸变。设$\mathbf{D}\in {\mathbb{R}}^{M\times N}$为得到的深度图。我们的校正方案在法线域中运行，因此我们从深度图中找到曲面法线，表示为${\mathbf{N}}^{\text{depth }}\in {\mathbb{R}}^{M\times N\times 3}$。粗深度图包含量化误差和噪声，因此应该使用鲁棒robust的方法，如[24,20]来获得法线。具体来说，我们选择[20]中引入的平面主成分分析技术，因为它具有鲁棒性(技术细节见补充)。

4.1.1 Removing low-frequency azimuthal ambiguity

考虑图3中的角落场景。使用粗深度传感器，获得表面的低频版本(注意图3b中三维形状的光滑性)。另一方面，由于方位角翻转，偏振法线的形状非常不准确，但高频细节可以恢复。

图3。常用的基准场景[13,29]。将偏振光技术与Kinect结合在一起可以提高性能。顶部一行显示了一个角落的3D形状。第二行显示表面法线。第三行以毫米为单位绘制表面误差估计值，第四行以w.r.t.度表示表面法线的角误差估计值。

​ 用${\mathbf{N}}^{\text{polar }}$表示由偏振线索得到的法线图。目标是找到一个与${\mathbf{N}}^{\text{polar }}$和${\mathbf{N}}^{\text{depth }}$相关的运算符$\mathcal{A}$，它可以用数字表示为$\mathcal{A}=\arg {\min }_{\mathcal{A}}{\Vert {\mathbf{N}}^{\text{depth }}-\mathcal{A}\left({\mathbf{N}}^{\text{polar }}\right)\Vert }_2^2$。==在没有附加约束的情况下，该优化是不适定的(ill-posed)。==然而，为了解决偏振模糊问题，我们只对将$\mathcal{A}$表示为二元线性算子感兴趣。这两种状态对应的是通过π旋转方位角，或者不是。由于目标是解决低频模糊，在总变化的意义上，我们施加了一个附加约束，即A是一个光滑算子。综合起来，这可以表示为一个总变差最小化问题:
$$\begin{array}{rl}\mathcal{A}=& \underset{\mathcal{A}}{\mathrm{argmin}}{\Vert {\mathbf{N}}^{\text{depth }}-\mathcal{A}\left({\mathbf{N}}^{\text{polar }}\right)\Vert }_2^2+\gamma \Vert \nabla \mathcal{A}{\Vert }_1\\ & \text{ subject to }\mathcal{A}\in \{0,1\},\end{array}\text{\hspace{1em}(5)}$$
其中参数$\gamma$控制(分段)平滑的解决方案。有许多知名的求解器可以解决这个优化程序。由于决策变量是二值的，所以我们使用图形切分(graph-cuts)，它通常用于将图像分割成前景和背景补丁。在得到$\mathcal{A}$后，我们可以通过对偏振法线应用算子来校正模糊度的低频变化:
$${\mathbf{N}}^{\text{corr }}=\mathcal{A}\left({\mathbf{N}}^{\text{polar }}\right)\text{\hspace{1em}(6)}$$
对低频模糊度进行校正后，我们可以回到角落的物理实验。通过应用本节介绍的技术，我们已经从图3g中模糊的法线到图3h中正确翻转的法线。在这个例子中，模糊度在本质上是低频率的，所以粗深度图就足够了。

4.1.2 Removing high-frequency azimuthal ambiguity

​ 如果深度图是粗糙的，由低频信息组成，则不能用于解决高频模糊区域。为了应对这一挑战，我们迫使表面的这些区域关闭。图4a示出在平面上具有高频V形槽(V-groove)的概念示例。法线可以在平面上正确消除模糊，但山脊无法使用4.1.1节的方法消除模糊。特别要注意的是，高频脊可以有六种形式之一。为了约束这个问题，我们在高频区域的起点定义一个锚点（Anchor Point），在脊的中心定义一个轴点（Pivot Point）。锚点代表高频脊的边界条件，枢轴点表示与面的前端平行的部分，即天顶角接近于零的地方。

​ 给定锚点和枢轴点，我们定义一个小面facet作为锚点和枢轴点之间的点集(见图4b)。一个小面可以形成一个平面的或非平面的表面。假设有K个facet，有$2\times 2^K-V$ 种可能的曲面构型，其中$V$是closed surfaces的数量。这个曲面有两个facet和两个closed surfaces，因此有六种可能的构型。其中4个是not closed，即高频区域在锚点处有不连续。不连续在物理上是可能的。在现实世界中，V形槽实际上可能是现实世界中的斜坡，但高频细节在锚点处具有这样的不连续性的可能性较小。 因此，我们假设高频表面是封闭的。

​ 在这两个闭合曲面中，一个是凹的，另一个是凸的。没有办法用偏振线索来区分这些表面。这并不是偏振增强所独有的：凸/凹模糊适用于SfS[33]和未经校准的PS[45]的整个表面。

图4。解决高频模棱两可。考虑一个带有高频凹坑的平面。(a)确定锚点和枢轴点，将模糊区域上的点组合成(b)面。©每个面都可以以π弧度旋转，从而产生歧义。

4.1.3 Correcting for refractive distortion

​ 回想一下，估计天顶角需要知道折射率。对于绝缘范围内的材料，估计天顶角的偏差只是一个很小的误差来源(图5)。然而，对于非绝缘材料，天顶角表面法线将被扭曲，这在集成时将导致三维形状的畸变。

​ 为了使天顶角不失真，我们首先找到深度图中能够很好地估计粗糙物体形状的区域。具体来说，我们将二进制掩码定义为
$$\mathbf{M}=1\text{ if }{\nabla }^T{\mathbf{N}}^{\text{depth }}\le ϵ\text{ and }{\nabla }^T{\mathbf{N}}^{\text{corr }}\le ϵ,\mathbf{M}=0\text{ o.w. }\text{\hspace{1em}(7)}$$
其中$ϵ$是平滑阈值。直观地说，掩模在确定区域取1的值，在这些区域中物体缺乏高频细节(由偏振法线决定)，在其他区域取0。对于图3中的转角，我们可以观察到转角的尖点，即由于多路径而导致Kinect数据不准确的地方，由于${\mathbf{N}}^{\text{corr }}$的散度较高而被掩盖了。

​ 令${\mathbf{\theta }}^{\text{depth }}$和${\mathbf{\theta }}^{\text{corr }}$表示第4.1.1节中${\mathbf{N}}^{\text{depth }}$和${\mathbf{N}}^{\text{corr }}$的天顶分量。在每个补丁patch,中，我们旋转修正后的法线，即$\mathcal{R}=\arg {\min }_{\mathcal{R}}{\Vert \mathbf{M}\odot {\mathbf{\theta }}^{\text{depth }}-\mathcal{R}\left({\mathbf{\theta }}^{\text{corr }}\right)\Vert }_2^2$。为了校正折射率，法线通过应用旋转操作（等式8）来更新
$${\mathbf{N}}^{\text{corr }}:=\mathcal{R}\left({\mathbf{N}}^{\text{corr }}\right)\text{\hspace{1em}(8)}$$

图5。在绝缘范围内(n=1.3 ~ 1.8)，折射率畸变对形状重构的影响很小(模拟实例)。我们用三个球体模拟了一个场景，每个球体都有不同的材料属性，但几何上是相同的。如果折射率未知(并且使用硬编码阈值)，则(a)-©底部一行所显示的估算的表面法线会出现轻微的扭曲。当对(a)-©的上排所示的表面进行积分时，形状稍有变化，如(d)所示。

4.2. Corrected normals from polarization to enhance the coarse depth map

​ 给出修正后的法线，就可以通过积分得到三维形状。不幸的是，众所周知，由于深度不连续，表面法向积分是一项具有挑战性的任务[1,48]。为了恢复合理的三维形状，我们开发了一种集成方案，将输入深度图$\text{ (D) }$和偏振的物理直觉 physical intuition$\left({\mathbf{N}}^{\text{corr }}\right)$结合起来，以恢复表面$\mathbf{D}\in {\mathbb{R}}^{M\times N}$的深度坐标。

4.2.1 Spanning tree constraint

​ 积分表面法线的标准方法是使用著名的泊松Poisson方程，为我们的问题写有${\nabla }^2\mathbf{D}={\nabla }^T{\mathbf{N}}^{\text{corr }}$。这是最小二乘意义上的最优解，并且在噪声模型是系统的情况下很有效。

​ 对于偏振问题，曲面法线存在系统误差。直观地说，避免使用不可靠的表面法线进行积分是可取的。特别地，只要在一个加权的二维图上使用最小生成树(生成树是用Kruskal的算法找到的)，曲面就可以以封闭的形式恢复。最优解写为
$${\nabla }_S^2\mathbf{D}={\nabla }_S^T{\mathbf{N}}^{\text{corr }}\text{\hspace{1em}(9)}$$
其中$S$为重建过程中使用的${\nabla }_S^2$和${\nabla }_S^T$代表在$S$上计算的拉普拉斯和散度算子，为了精确积分，该集合$S$包含了图的生成树。设${\mathbf{W}}_{x,y}$为二维网格的权值。为了找到权重，大多数以前的工作使用随机抽样、梯度大小或对可积性的约束[1,8]。

​ 利用偏振的物理特性来激励图权的选择。具体来说，当偏振程度ρ值较低时，偏振法线被认为是有噪声的

低偏振度通常发生在天顶角接近于零时(即平行面)。对于深度图，4.1.3节定义的掩模算子(mask operator)$M$提供了一个置信度权重。

​ 我们将积分中使用的梯度集$S$初始化为空集。第一个加入到$S$中的梯度是那些位于有权图的最小生成树上的梯度:
$$\mathbf{W}=\rho \text{ if }\rho >\tau \text{ and }\mathbf{M}=0,\mathbf{W}=\tau \text{ otherwise }\text{\hspace{1em}(10)}$$
其中$\tau$反映了偏振和深度法线的置信水平。然后，我们使用[1]中描述的迭代$\alpha$-方法更新$S$，并添加了${\mathbf{N}}^{\text{corr }}$和 ${\mathbf{N}}^{\text{depth }}$在更新过程中。最后，我们将修正后的法线更新为
$${\mathbf{N}}_{x,y}^{\text{corr }}:={\mathbf{N}}_{x,y}^{\text{depth }}\text{ if }{\mathbf{W}}_{x,y}\le \tau \text{\hspace{1em}(11)}$$

4.2.2 Depth fidelity constraint

​ 当对曲面法线进行积分时，只会得到一个相对的三维形状，但其偏移量和尺度是未知的。在这里，深度保真约束用于保存全局坐标系统，并加强集成表面和深度地图的精确区域之间的一致性。具体地说，深度约束的形式是
$$\Vert \mathbf{M}\odot (\mathbf{D}-\mathbf{D}){\Vert }_2^2\text{\hspace{1em}(12)}$$
在这里，我们使用了与掩码相结合的元素乘法，只有在深度图可靠的情况下，才能增强保真度。深度保真度和生成树约束都被纳入一个稀疏线性系统
$$\left[\begin{array}{c}\lambda \mathbf{M}\odot \mathbf{I}\\ {\nabla }_S^2\end{array}\right]\mathrm{VEC}(\mathbf{D})=\left[\begin{array}{c}\lambda \mathrm{VEC}(\mathbf{M}\odot \mathbf{D})\\ {\nabla }_S^T\left({\mathbf{N}}^{\text{corr }}\right)\end{array}\right]\text{\hspace{1em}(13)}$$
其中$VEC$为向量化算子，$I$为单位矩阵，大小为$MN\times MN$， $\lambda$为标量参数，用于调整生成树与深度保真约束之间的权衡。关于求解器的详细信息，请参见附录。

5. Assessment and Results

​ 在具有挑战性的材料或照明条件下，先前的遮阳增强技术的成功有限。所提出的技术，利用偏振，能够处理更复杂的场景。

5.1. Robustness in the wild

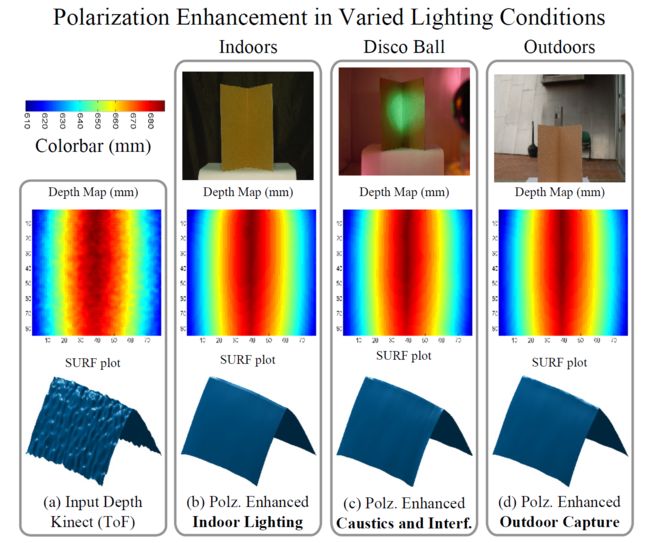
Robustness to lighting conditions对照明条件的鲁棒性：假设在入射光为非偏振的情况下，该方法对不同的光照条件具有较强的鲁棒性。如图6所示，在以下三种光照条件下，深度增强效果几乎相同:(图6b)室内光照;(图6c)迪斯科球干扰下的照明;(图6d)即使是在户外。后两个条件违反了SfS的照明假设。

图6。偏振增强工作在一系列的光照条件下(真实的实验)。(a) ToF Kinect由于多路径，无法准确捕捉角。(b)室内偏振增强。©迪斯科灯光下的偏振增强。迪斯科球投射方向不均匀的光线到角落，并引入腐蚀剂效果。(d)冬季部分晴天的户外偏振增强。

Robustness to material properties对材料性能的鲁棒性：如图7所示，在三种材料上对所提出的技术进行了评估:(1)漫反射;(2)光泽;和(3)镜面。偏振增强对于每一种材料都是一致的，尽管对于像镜子的物体稍微差一些。使用阴影增强的比较论文只适用于传感器的表面 Lambertian surface[44,14,43,34]。

图7。偏振增强工作在各种物质条件下。使用噪声深度骨架作为深度模板，并通过细化技术恢复所有材料的球体。

Robustness to diffuse multipath对扩散多路径的鲁棒性：弥漫性多径Diffuse multipath一直是ToF社区的一个积极挑战[35,13,29]。本文提出的偏振增强技术大大优于目前最先进的多径校正技术，同时使用更少的图像[29]。详见图8的说明。

图8。该方法可以有效地消除ToF传感器中的多径干扰。将所提出的技术与Naik等人的[29]进行比较，后者将ToF与投影机的结构化照明模式相结合。Naik等人的技术使用了25张编码照明照片。通过用偏振器拍摄的3张照片和Kinect深度图，所提出的技术保留了地面真相的尖锐边缘。

5.2. Results on various scenes

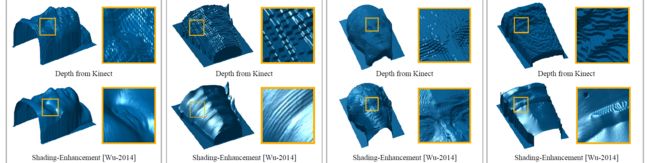
​ 图9显示了其他结果，以及Wu等人直接进行的与阴影细化的定性比较。

Diffuse face scene分散的脸场景：我们选择如图9a所示的人体场景，比较遮光增强的最佳情况与我们提出的偏振增强技术的性能。具体来说，人体模型被涂上漫反射漆，并被远处的灯光照亮，以符合SfS的假设。即使在理想的条件下，阴影细化，提出的技术使用偏振导致轻微改善三维重建。如特写所示，凹眼窝由于漫反射引起的阴影细化的挑战。

Coffee cup scene咖啡杯场景：图9b为泡沫塑料咖啡杯深度重建图。这样的表面不是朗伯式的，并且会导致阴影细化的伪影。所提出的技术明显优于阴影细化，并且正如特写镜头所示，能够清晰地恢复沟槽(300微米特征尺寸)。对于这个场景，提出的技术优于激光扫描对象(比较见补充)。

Two-face scene双面人场景：为了说明对混合材料的鲁棒性，图9c显示了一个模特儿，用两种不同颜料和高光性的颜料绘制。遮光增强不能处理面部的光泽，因此整个重建效果较差。此外，在材料转换的点上，当地的人工制品是可见的(最好在特写中看到)。相比之下，偏振增强技术可以很好地恢复地表，并且对物质变化具有鲁棒性(见特写)。注意，在材料过渡点缺少伪影验证了假设4不需要严格(因为油漆有不同比例的漫反射和镜面反射率)。

Trash can scene垃圾桶场景：图9d描绘了自然光照下的日常物体场景。这个场景包括一个坚硬的塑料垃圾桶，有一个闪闪发光的塑料衬垫，在一个有窗户的照明良好的机械车间。这是一个具有挑战性的场景深度增强，与失控的照明，混合材料和高光物体。所提出的技术比着色细化要好得多。 特别是，通过阴影细化进行的重建在恢复的曲面中包含与图像中的镜面高光相对应的孔。 此外，由于衬里高度镜面反射，因此遮光效果无法解决山脊的问题。

图9。各种各样的捕捉，从控制的场景到复杂的场景。请使用PDF浏览器放大。

5.3. Quantitative analysis of enhancement

​ 表2显示了平均绝对误差wrt。本文中场景采样的激光扫描。由于基于阴影的技术[43]无法处理诸如铬球或有光泽的咖啡杯之类的发亮物体，因此误差实际上会增加wrt。输入深度。相反，所提出的偏振技术减少了所有场景的误差。因为偏振可以处理交互反射(Kinect不能)，偏振在角落场景中表现出最大的改进。参考图3以获得更多的参数。

​ 为了验证所提方法的分辨率增强效果，我们使用精密卡尺测量了图9c中300微米处的杯形沟槽。与某些激光扫描器相比，该技术能够更精确地分辨细节。

5.4. Implementation details

​ 如图2所示，捕获设置包括以下内容:佳能Rebel T3i单反相机，标准的佳能EF-S 18-55mm f/3.5-5.6 IS II单反镜头，1 / 4波片的线性偏光镜，型号Hoya cirpl。在偏振器的传动轴上进行标定。对于所有场景，$\tau$和$ϵ$的值是相同的。最常用的深度地图是最新款的微软Kinect。法线贴图和深度贴图使用Kinect的内在参数和相对姿态(仅限翻译)进行注册。为了测量偏振线索，传感器响应必须是线性的，强制通过预处理来自相机的CR2原始文件。真值Ground truth是通过多条纹，三角测量，激光扫描仪和基准是通过ICPLaser Scanner 。源代码、数据集和运行时细节可以在项目网页上找到

6. Discussion

​ 总之，我们提出了第一种利用偏振法线进行深度增强的技术。尽管阴影细化是一个既定领域，但随着每年的进步，所提出的技术利用不同的物理特性来展示互补的优势。

Benefits：通过使用深度图在偏振形状问题上放置许多限制，本文解决了以前偏振形状研究中的许多歧异，同时展示了与替代技术(SfS和PS)相比的令人信服的优势。特别地，SfS和PS假设朗伯物体和远程/控制照明，而提出的技术已经证明了在可控和不可控的设置下漫反射到镜面状物体的结果。此外，本文提出的技术可以是被动的，可以在一次拍摄中实现，并且不需要基线(表1)。虽然本文的技术不是针对多径校正，但使用的图像较少，其性能优于一篇专门研究ToF多径校正的论文(图8)。

Limitations：该技术需要采集3张图像；然而，现成的解决方案Polarization mosaic允许单次捕获。为了稳健的性能，必须满足第4节和表1中的假设。请注意，其中一些限制也存在于SfS和PS上下文中。例如，所提出的技术不能处理高光互反射，而SfS或PS方法不能处理漫反射或高光互反射。

Open challenges：虽然所提出的技术能够获得令人鼓舞的结果(如图9d)，但仍存在一些科学挑战，包括:（1）更好的方法来计算偏振法线现场方面包含漫反射和镜面反射的混合物(看到脚注1, 2),（2）是否有一种方法可以正确地解决高频细节不必诉诸封闭曲面启发式(Sec 4.1.2),和（3）备用方式规避低程度的极化fronto-parallel方面(Sec 4.2.1)准备。额外的信息，例如，来自多视图数据，圆偏振，或阴影，可能是改进我们技术的一种方式。总之，我们希望我们的实际结果能激发人们对使用偏振进行3D传感的兴趣。