线性系统大作业——2.二阶倒立摆建模与控制系统设计(上)
文章目录
- 0.简介
- 1.建立数学模型
-
- 1.1.牛顿运动定律分析
-
- 欧拉-拉格朗日方程分析
- 2.Simulink仿真
- 3.使用SimMechancis仿真
- 4.在平衡点附近模型线性化
- 5.系统能控性、能观性和稳定性分析
-
- 5.1.能控性分析
- 5.2.能观性分析
- 5.3.稳定性分析
-
- 5.3.1.Routh-Hurwitz判据
-
- Lyapunov函数
- 6.基于极点配置方法的控制器设计
0.简介
本文是《线性系统理论》大作业的一部分,内容是一阶和二阶倒立摆的分析与控制,本文是 线性系统大作业——0.一阶和二阶倒立摆建模与控制系统设计 的一部分。
另外,由于本文字数过多,超过了CSDN单篇文章的字数限制,因此将本文分成了上下两部分。下半部分见:线性系统大作业——2.二阶倒立摆建模与控制系统设计(下)
最后,本文中使用的 MATLAB 代码和 Simulink 仿真模型已经上传到 GitHub 上。
Code: https://github.com/Cc19245/Inverted-pendulum.git
1.建立数学模型

给定二阶倒立摆的物理模型如图所示,给出系统的参数如表所示,假设两杆的质量都是均匀分布的,并且不考虑系统的摩擦。
| 物理量 | 数值 |
|---|---|
| 小车质量( M M M) | 2 k g 2kg 2kg |
| 下杆质量( m 1 m_1 m1) | 0.5 k g 0.5kg 0.5kg |
| 上杆质量( m 2 m_2 m2) | 0.5 k g 0.5kg 0.5kg |
| 下杆长度( L L L) | 0.4 m 0.4m 0.4m |
| 上杆长度( L L L) | 0.4 m 0.4m 0.4m |
1.1.牛顿运动定律分析
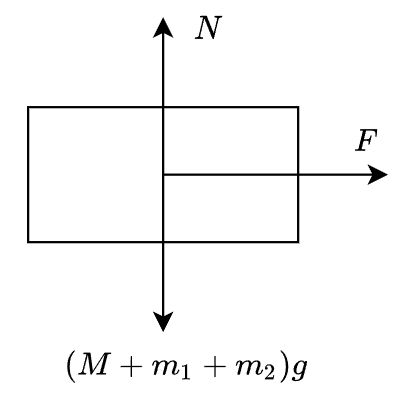
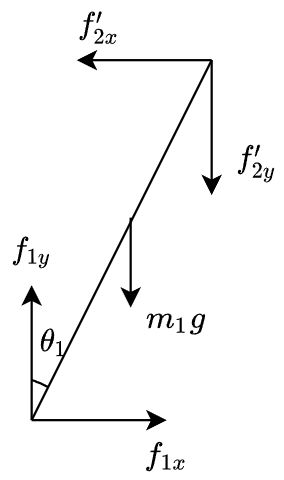
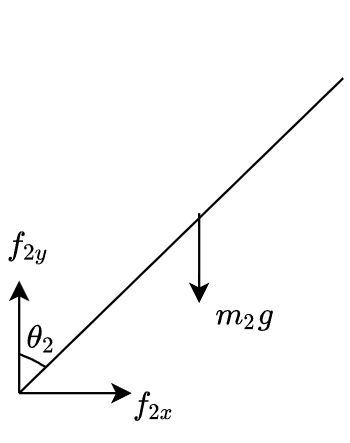
对整个系统、下摆杆和上摆杆进行受力分析分别如图所示。
上摆杆和下摆杆的质心坐标为 x 1 g = x + l 1 sin θ 1 y 1 g = l 1 cos θ 1 x 2 g = x + L sin θ 1 + l 2 sin θ 2 y 2 g = L cos θ 1 + l 2 cos θ 2 \begin{aligned} \begin{array}{cccc} &x_{1 g}=x+l_{1} \sin \theta_{1} \\ &y_{1 g}=l_{1} \cos \theta_{1} \\ &x_{2 g}=x+L \sin \theta_{1}+l_{2} \sin \theta_{2} \\ &y_{2 g}=L \cos \theta_{1}+l_{2} \cos \theta_{2} \end{array} \end{aligned} x1g=x+l1sinθ1y1g=l1cosθ1x2g=x+Lsinθ1+l2sinθ2y2g=Lcosθ1+l2cosθ2
首先对系统进行整体的受力分析,在水平方向有 F = M x ¨ + m 1 ∂ 2 ( x 1 g ) ∂ t 2 + m 2 ∂ 2 ( x 2 g ) ∂ t 2 \begin{aligned} F =M\ddot{x}+m_{1} \frac{\partial^{2}\left(x_{1 g}\right)}{\partial t^{2}}+m_{2} \frac{\partial ^{2}\left(x_{2 g}\right)}{\partial t^{2}} \end{aligned} F=Mx¨+m1∂t2∂2(x1g)+m2∂t2∂2(x2g)
对下摆杆在惯性系下受力分析,则下摆杆还受到自身加速度引起的惯性力,由动量矩定理,有
f 2 y ′ L sin θ 1 + m 1 g l 1 sin θ 1 − f 2 x ′ L cos θ 1 − m 1 x ¨ 1 g l 1 cos θ 1 + m 1 y ¨ 1 g l 1 sin θ 1 = I 1 θ ¨ 1 \begin{aligned} &f_{2 y}^{\prime} L \sin \theta_{1}+m_{1} g l_{1} \sin \theta_{1}-f_{2 x}^{\prime} L \cos \theta_{1}-m_{1} \ddot{x}_{1 g} l_1 \cos \theta_{1}+m_{1} \ddot{y}_{1 g} l_1 \sin \theta_{1}=I_{1} \ddot{\theta}_{1} \end{aligned} f2y′Lsinθ1+m1gl1sinθ1−f2x′Lcosθ1−m1x¨1gl1cosθ1+m1y¨1gl1sinθ1=I1θ¨1
同理对上摆杆,有 m 2 g l 2 sin θ 2 − m 2 l 2 cos θ 2 x ¨ 2 g + m 2 l 2 sin θ 2 y ¨ 2 g = I 2 θ ¨ 2 \begin{aligned} m_{2} g l_{2} \sin \theta_{2}-m_{2} l_{2} \cos \theta_{2} \ddot{x}_{2 g}+m_{2} l_{2} \sin \theta_{2} \ddot{y}_{2 g}=I_{2} \ddot{\theta}_{2} \end{aligned} m2gl2sinθ2−m2l2cosθ2x¨2g+m2l2sinθ2y¨2g=I2θ¨2
对上摆杆,在水平方向和竖直方向进行受力分析,由牛顿运动定律可得
f 2 x = m 2 x ¨ 2 g = m 2 ( x + L sin θ 1 + l 2 sin θ 2 ) ′ ′ f 2 y − m 2 g = m 2 y ¨ 2 g = m 2 ( L cos θ 1 + l 2 cos θ 2 ) ′ ′ \begin{aligned} \begin{array}{c} f_{2 x}=m_{2} \ddot{x}_{2 g}=m_{2}\left(x+L \sin \theta_{1}+l_{2} \sin \theta_{2}\right)^{''} \\ f_{2 y} - m_2g=m_{2} \ddot{y}_{2 g}=m_{2}\left(L \cos \theta_{1}+l_{2} \cos \theta_{2}\right)^{''} \end{array} \end{aligned} f2x=m2x¨2g=m2(x+Lsinθ1+l2sinθ2)′′f2y−m2g=m2y¨2g=m2(Lcosθ1+l2cosθ2)′′
将式带入式可得 ( M + m 1 + m 2 ) x ¨ + ( m 1 l 1 + m 2 L ) cos θ 1 ⋅ θ ¨ 1 + m 2 l 2 cos θ 2 ⋅ θ ¨ 2 − ( M 1 l 1 + M 2 L ) sin θ 1 ⋅ θ ˙ 1 2 − M 2 l 2 sin θ 2 ⋅ θ ˙ 2 2 = F \begin{aligned} \begin{array}{cc} &\left(M+m_{1}+m_{2}\right) \ddot{x}+\left(m_{1} l_{1}+m_{2} L\right) \cos \theta_{1} \cdot \ddot{\theta}_{1}+m_{2} l_{2} \cos \theta_{2} \cdot \ddot{\theta}_{2} \\ &-\left(M_{1} l_{1}+M_{2} L\right) \sin \theta_{1} \cdot \dot{\theta}_{1}^{2}-M_{2} l_{2} \sin \theta_{2} \cdot \dot{\theta}_{2}^{2}=F \end{array} \end{aligned} (M+m1+m2)x¨+(m1l1+m2L)cosθ1⋅θ¨1+m2l2cosθ2⋅θ¨2−(M1l1+M2L)sinθ1⋅θ˙12−M2l2sinθ2⋅θ˙22=F
将式和式带入式,可得 ( m 1 l 1 + m 2 L ) cos θ 1 ⋅ x ¨ + ( I 1 + m 1 l 1 2 + m 2 L 2 ) θ ¨ 1 + m 2 L l 2 cos ( θ 2 − θ 1 ) ⋅ θ ¨ 2 − m 2 L l 2 sin ( θ 2 − θ 1 ) ⋅ θ ˙ 2 2 = ( m 1 l 1 + m 2 L ) g sin θ 1 \begin{aligned} \begin{array}{cc} &\left(m_{1} l_{1}+m_{2} L\right) \cos \theta_{1} \cdot \ddot{x}+\left(I_{1}+m_{1} l_{1}^{2}+m_{2} L^{2}\right) \ddot{\theta}_{1}+m_{2} L l_{2} \cos \left(\theta_{2}-\theta_{1}\right) \cdot \ddot{\theta}_{2} \\ &-m_{2} L l_{2} \sin \left(\theta_{2}-\theta_{1}\right) \cdot \dot{\theta}_{2}^{2}=\left(m_{1} l_{1}+m_{2} L\right) g \sin \theta_{1} \end{array} \end{aligned} (m1l1+m2L)cosθ1⋅x¨+(I1+m1l12+m2L2)θ¨1+m2Ll2cos(θ2−θ1)⋅θ¨2−m2Ll2sin(θ2−θ1)⋅θ˙22=(m1l1+m2L)gsinθ1
将式和式带入式,可得 m 2 l 2 cos θ 2 ⋅ x ¨ + m 2 L l 2 cos ( θ 2 − θ 1 ) ⋅ θ ¨ 1 + ( I 2 + m 2 l 2 2 ) θ ¨ 2 + m 2 L l 2 sin ( θ 2 − θ 1 ) ⋅ θ ˙ 1 2 = m 2 g l 2 sin θ 2 \begin{aligned} \begin{array}{cc} &m_{2} l_{2} \cos \theta_{2} \cdot \ddot{x}+m_{2} L l_{2} \cos \left(\theta_{2}-\theta_{1}\right) \cdot \ddot{\theta}_{1}+\left(I_{2}+m_{2} l_{2}^{2}\right) \ddot{\theta}_{2} \\ &+m_{2} L l_{2} \sin \left(\theta_{2}-\theta_{1}\right) \cdot \dot{\theta}_{1}^{2}=m_{2} g l_{2} \sin \theta_{2} \end{array} \end{aligned} m2l2cosθ2⋅x¨+m2Ll2cos(θ2−θ1)⋅θ¨1+(I2+m2l22)θ¨2+m2Ll2sin(θ2−θ1)⋅θ˙12=m2gl2sinθ2
则由上述三式组成的方程组即为二阶倒立摆的动力学方程。
欧拉-拉格朗日方程分析
选择小车位移 x x x和两个摆杆的角度 θ 1 \theta_1 θ1和 θ 2 \theta_2 θ2作为广义坐标,小车推理 F F F作为广义力,则有
T M = 1 2 M r ˙ 2 T m 1 = 1 2 I 1 θ ˙ 1 2 + 1 2 m 1 × { [ d d t ( r + l 1 sin θ 1 ) ] 2 + [ d d t ( l 1 cos θ 1 ) ] 2 } = 1 2 I 1 θ ˙ 1 2 + 1 2 m 1 × [ ( r ˙ + l 1 cos θ 1 ⋅ θ ˙ 1 ) 2 + ( l 1 sin θ 1 ⋅ θ ˙ 1 ) 2 ] T m 2 = 1 2 I 2 θ ˙ 2 2 + 1 2 m 2 × { [ d d t ( r + L 1 sin θ 1 + l 2 sin θ 2 ) ] 2 + [ d d t ( L 1 cos θ 1 + l 2 cos θ 2 ) ] 2 } = 1 2 I 2 θ ˙ 2 2 + 1 2 m 2 × [ ( r ˙ + L 1 cos θ 1 ⋅ θ ˙ 1 + l 2 cos θ 2 ⋅ θ ˙ 2 ) 2 + ( L 1 sin θ 1 ⋅ θ ˙ 1 + l 2 sin θ 2 ⋅ θ ˙ 2 ) 2 ] V M = 0 V m 1 = m 1 g l 1 cos θ 1 V m 2 = m 2 g × ( L 1 cos θ 1 + l 2 cos θ 2 ) \begin{aligned} \begin{aligned} T_{M} &=\frac{1}{2} M \dot{r}^{2} \\ T_{m_1} &=\frac{1}{2} I_{1} \dot{\theta}_{1}^{2}+\frac{1}{2} m_{1} \times\left\{\left[\frac{d}{d t}\left(r+l_{1} \sin \theta_{1}\right)\right]^{2}+\left[\frac{d}{d t}\left(l_{1} \cos \theta_{1}\right)\right]^{2}\right\} \\ &=\frac{1}{2} I_{1} \dot{\theta}_{1}^{2}+\frac{1}{2} m_{1} \times\left[\left(\dot{r}+l_{1} \cos \theta_{1} \cdot \dot{\theta}_{1}\right)^{2}+\left(l_{1} \sin \theta_{1} \cdot \dot{\theta}_{1}\right)^{2}\right] \\ T_{m_2} &=\frac{1}{2} I_{2} \dot{\theta}_{2}^{2}+\frac{1}{2} m_{2} \times\left\{\left[\frac{d}{d t}\left(r+L_{1} \sin \theta_{1}+l_{2} \sin \theta_{2}\right)\right]^{2}+\left[\frac{d}{d t}\left(L_{1} \cos \theta_{1}+l_{2} \cos \theta_{2}\right)\right]^{2}\right\} \\ &=\frac{1}{2} I_{2} \dot{\theta}_{2}^{2}+\frac{1}{2} m_{2} \times\left[\left(\dot{r}+L_{1} \cos \theta_{1} \cdot \dot{\theta}_{1}+l_{2} \cos \theta_{2} \cdot \dot{\theta}_{2}\right)^{2}+\left(L_{1} \sin \theta_{1} \cdot \dot{\theta}_{1}+l_{2} \sin \theta_{2} \cdot \dot{\theta}_{2}\right)^{2}\right] \\ V_{M} &=0 \\ V_{m_1} &=m_{1} g l_{1} \cos \theta_{1} \\ V_{m_2} &=m_{2} g \times\left(L_{1} \cos \theta_{1}+l_{2} \cos \theta_{2}\right) \end{aligned}\end{aligned} TMTm1Tm2VMVm1Vm2=21Mr˙2=21I1θ˙12+21m1×{[dtd(r+l1sinθ1)]2+[dtd(l1cosθ1)]2}=21I1θ˙12+21m1×[(r˙+l1cosθ1⋅θ˙1)2+(l1sinθ1⋅θ˙1)2]=21I2θ˙22+21m2×{[dtd(r+L1sinθ1+l2sinθ2)]2+[dtd(L1cosθ1+l2cosθ2)]2}=21I2θ˙22+21m2×[(r˙+L1cosθ1⋅θ˙1+l2cosθ2⋅θ˙2)2+(L1sinθ1⋅θ˙1+l2sinθ2⋅θ˙2)2]=0=m1gl1cosθ1=m2g×(L1cosθ1+l2cosθ2)
将上述变量带入欧拉-拉格朗日方程,化简可得系统数学模型为
[ M 11 M 12 M 13 M 21 M 22 M 23 M 31 M 32 M 33 ] [ x ¨ θ ¨ 1 θ ¨ 2 ] + [ C 11 C 12 C 13 C 21 C 22 C 23 C 31 C 32 C 33 ] [ x ˙ θ ˙ 1 θ ˙ 2 ] + [ G 1 G 2 G 3 ] = [ u 0 0 ] \begin{aligned} \begin{array}{l} {\left[\begin{array}{lll} M_{11} & M_{12} & M_{13} \\ M_{21} & M_{22} & M_{23} \\ M_{31} & M_{32} & M_{33} \end{array}\right]\left[\begin{array}{c} \ddot{x} \\ \ddot{\theta}_{1} \\ \ddot{\theta}_{2} \end{array}\right]+} {\left[\begin{array}{lll} C_{11} & C_{12} & C_{13} \\ C_{21} & C_{22} & C_{23} \\ C_{31} & C_{32} & C_{33} \end{array}\right]\left[\begin{array}{c} \dot{x} \\ \dot{\theta}_{1} \\ \dot{\theta}_{2} \end{array}\right]+\left[\begin{array}{c} G_{1} \\ G_{2} \\ G_{3} \end{array}\right]=\left[\begin{array}{c} u \\ 0 \\ 0 \end{array}\right] } \end{array}\end{aligned} ⎣⎡M11M21M31M12M22M32M13M23M33⎦⎤⎣⎡x¨θ¨1θ¨2⎦⎤+⎣⎡C11C21C31C12C22C32C13C23C33⎦⎤⎣⎡x˙θ˙1θ˙2⎦⎤+⎣⎡G1G2G3⎦⎤=⎣⎡u00⎦⎤
其中, M 11 = M + m 1 + m 2 M 12 = ( m 1 l 1 + m 2 L ) cos θ 1 M 13 = m 2 l 2 cos θ 2 M 21 = M 12 M 22 = I 1 + m 1 l 1 2 + m 2 L 2 M 23 = m 2 L l 2 cos ( θ 2 − θ 1 ) M 31 = M 13 M 32 = M 23 M 33 = I 2 + m 2 l 2 2 C 11 = 0 , C 12 = − ( m 1 l 1 + m 2 L ) θ ˙ 1 sin θ 1 , C 13 = − m 2 l 2 θ ˙ 2 sin θ 2 C 21 = 0 , C 22 = 0 , C 23 = − m 2 L l 2 θ ˙ 2 sin ( θ 2 − θ 1 ) C 31 = 0 , C 32 = m 2 L l 2 θ ˙ 1 sin ( θ 2 − θ 1 ) , C 33 = 0 G 1 = 0 , G 2 = − ( m 1 l 1 + m 2 L ) g sin θ 1 , G 3 = − m 2 g l 2 sin θ 2 u = F \begin{aligned} \begin{array}{l} M_{11}=M+m_{1}+m_{2} \\ M_{12}=\left(m_{1} l_{1}+m_{2} L\right) \cos \theta_{1} \\ M_{13}=m_{2} l_{2} \cos \theta_{2} \\ M_{21}=M_{12} \\ M_{22}= I_1 + m_{1} l_{1}^{2} + m_{2} L^{2} \\ M_{23}=m_{2} L l_{2} \cos \left(\theta_{2}-\theta_{1}\right) \\ M_{31}=M_{13} \\ M_{32}=M_{23} \\ M_{33} = I_{2} + m_{2} l_{2}^{2} \\ C_{11}=0, C_{12}=-\left(m_{1} l_{1}+m_{2} L\right) \dot{\theta}_{1} \sin \theta_{1}, C_{13}=-m_{2} l_{2} \dot{\theta}_{2} \sin \theta_{2}\\ C_{21}=0, C_{22}=0, C_{23}=-m_{2} L l_{2} \dot{\theta}_{2} \sin \left(\theta_{2}-\theta_{1}\right) \\ C_{31}=0, C_{32}=m_{2} L l_{2} \dot{\theta}_{1} \sin \left(\theta_{2}-\theta_{1}\right), C_{33}=0 \\ G_{1}=0, G_{2}=-\left(m_{1} l_{1}+m_{2} L\right) g \sin \theta_{1}, G_{3}=-m_{2} g l_{2} \sin \theta_{2} \\ u=F \end{array} \end{aligned} M11=M+m1+m2M12=(m1l1+m2L)cosθ1M13=m2l2cosθ2M21=M12M22=I1+m1l12+m2L2M23=m2Ll2cos(θ2−θ1)M31=M13M32=M23M33=I2+m2l22C11=0,C12=−(m1l1+m2L)θ˙1sinθ1,C13=−m2l2θ˙2sinθ2C21=0,C22=0,C23=−m2Ll2θ˙2sin(θ2−θ1)C31=0,C32=m2Ll2θ˙1sin(θ2−θ1),C33=0G1=0,G2=−(m1l1+m2L)gsinθ1,G3=−m2gl2sinθ2u=F
由此可见,使用欧拉-拉格朗日方程建立的系统动力学方程和使用牛顿运动定律建立的动力学方程是完全相同的,因此初步验证了所建立的动力学方程的正确性。
2.Simulink仿真
由二阶倒立摆系统的动力学方程可以发现,系统存在非常严重的耦合现象,因此直接使用Simulink搭建仿真模型较为麻烦,因此这里使用S-Fuction来建立系统的仿真模型。编写MATLAB代码实现如下:
% 二阶倒立摆系统的动力学方程s-function建模
function [sys,x0,str,ts,simStateCompliance] =
order2_sfun(t,x,u,flag, x_0, theta1_0, theta2_0)
switch flag,
case 0,
[sys,x0,str,ts,simStateCompliance]=
mdlInitializeSizes(t,x,u, x_0, theta1_0, theta2_0);
case 1,
sys=mdlDerivatives(t,x,u);
case 2,
sys=mdlUpdate(t,x,u);
case 3,
sys=mdlOutputs(t,x,u);
case 4,
sys=mdlGetTimeOfNextVarHit(t,x,u);
case 9,
sys=mdlTerminate(t,x,u);
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag',
num2str(flag));
end
% 主函数结束
% ---------------------------------------------
function [sys,x0,str,ts,simStateCompliance]=
mdlInitializeSizes(t,x,u, x_0, theta1_0, theta2_0)
% 初始化
sizes = simsizes;% 生成sizes数据结构
sizes.NumContStates = 6;% 连续状态数, 分别是x', theta1', theta2', x, theta1, theta2
sizes.NumDiscStates = 0;% 离散状态数,缺省为 0
sizes.NumOutputs = 6;% 输出量个数,缺省为 0,
sizes.NumInputs = 1;% 输入量个数,缺省为 0
sizes.DirFeedthrough = 1;%是否存在直接馈通。1:存在;0:不存在,缺省为 1
sizes.NumSampleTimes = 1; % at least one sample time is needed
sys = simsizes(sizes);
x0 = [0; 0; 0; x_0; theta1_0; theta2_0];% 设置初始状态
str = [];% 保留变量置空
ts = [0 0]; % 连续系统
simStateCompliance = 'UnknownSimState';
% end mdlInitializeSizes
% ---------------------------------------------
function sys=mdlDerivatives(t,x,u)
% 计算导数例程子函数
M=2; m1=0.5; m2=0.5; l1=0.2; l2=0.2; L=0.4; g=9.8
I1 = 1/12*m1*(2*l1)^2; I2 = 1/12*m2*(2*l2)^2;
dx_ = x(1); dth1_ = x(2); dth2_ = x(3);
x_ = x(4); th1_ = x(5); th2_ = x(6);
M11 = M + m1 + m2;
M12 = (m1*l1+m2*L)*cos(th1_);
M13 = m2*l2*cos(th2_);
M21 = M12;
M22 = I1 + m1*l1^2 + m2*L^2;
M23 = m2*L*l2*cos(th2_ - th1_);
M31 = M13;
M32 = M23;
M33 = I2 + m2*l2^2;
C11 = 0; C12 = -(m1*l1+m2*L)*sin(th1_)*dth1_;
C13 = -m2*l2*sin(th2_)*dth2_;
C21 = 0; C22 = 0; C23 = -m2*L*l2*dth2_*sin(th2_ - th1_);
C31 = 0; C32 = m2*L*l2*dth1_*sin(th2_ - th1_); C33 = 0;
G1 = 0; G2 = -(m1*l1+m2*L)*g*sin(th1_);
G3 = -m2*g*l2*sin(th2_);
A = [M11 M12 M13 C11 C12 C13;
M21 M22 M23 C21 C22 C23;
M31 M32 M33 C31 C32 C33;
0 0 0 1 0 0 ;
0 0 0 0 1 0 ;
0 0 0 0 0 1 ];
B = [u-G1;
-G2;
-G3;
dx_;
dth1_;
dth2_];
sys = A\B;
% ---------------------------------------------
function sys=mdlUpdate(t,x,u)
%3. 状态更新例程子函数
sys = [];
% ---------------------------------------------
function sys=mdlOutputs(t,x,u)
%4. 计算输出例程子函数
sys=[x(1);x(2);x(3);x(4);x(5);x(6)];
% ---------------------------------------------
function sys=mdlGetTimeOfNextVarHit(t,x,u)
% 5. 计算下一个采样时间,仅在系统是变采样时间系统时调用
sampleTime = 1; % Example, set the next hit to be one second later.
sys = t + sampleTime;
% ---------------------------------------------
function sys=mdlTerminate(t,x,u)
% 6. 仿真结束时要调用的例程函数
sys = [];
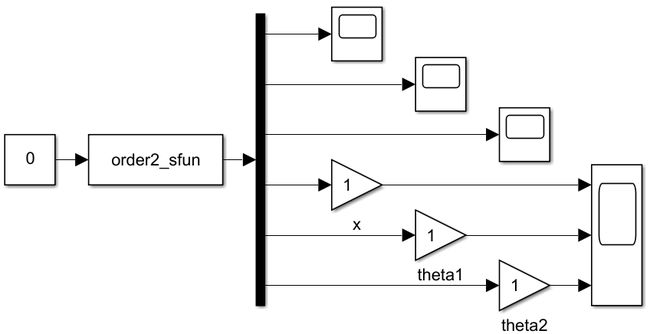
利用s-function在Simulink中搭建系统的仿真模型如图所示。
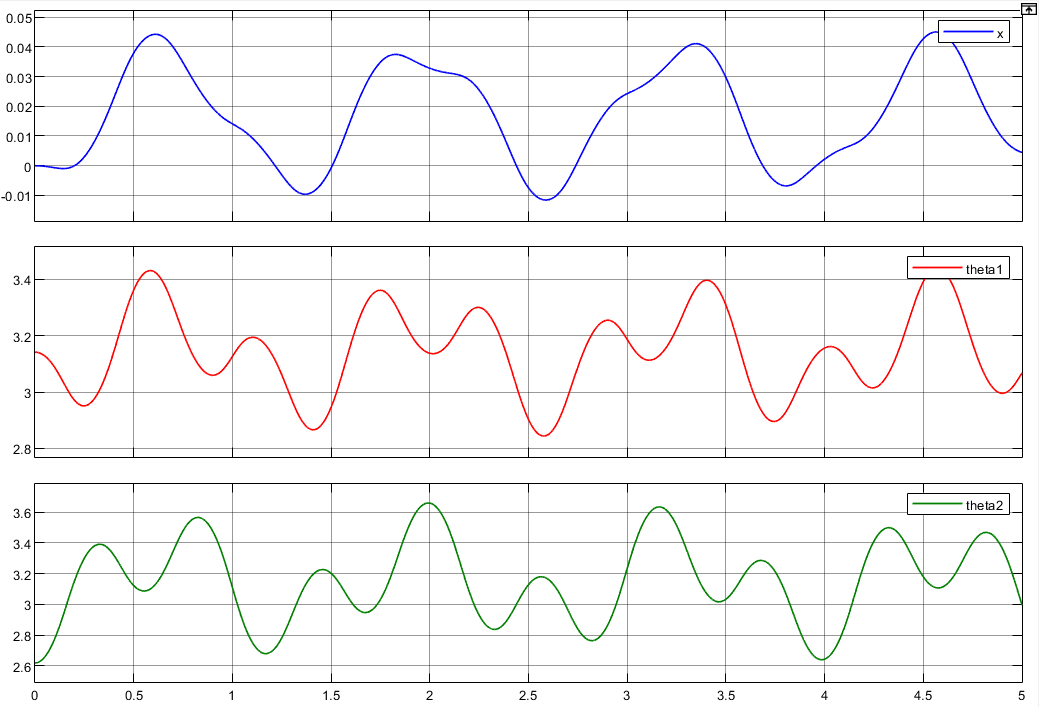
由于二阶倒立摆很不稳定,所以为了看系统初始状态下存在小扰动时系统的动态响应,假设系统的初始状态偏离渐进稳定点,即 x = 0 , θ 1 = π , θ 2 = 5 6 π x=0,\theta_1=\pi,\theta_2=\frac{5}{6}\pi x=0,θ1=π,θ2=65π,且系统无输入,则此后小车位置 x x x和倒立摆的摆角 θ 1 \theta_1 θ1、 θ 2 \theta_2 θ2的变化如图所示。
3.使用SimMechancis仿真
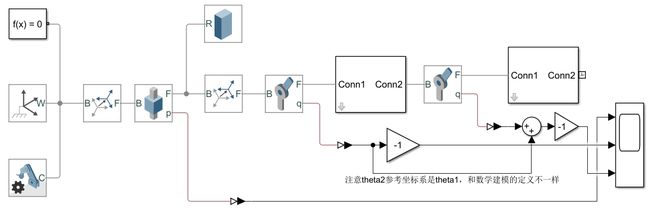
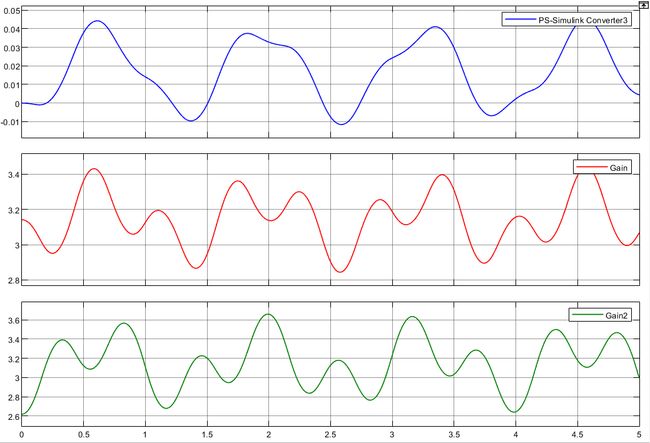
如图所示,是使用SimMechanicalcs建立二阶倒立摆的物理模型。其中增益模块的增益值-1是由于SimMechanicalcs中的 θ \theta θ方向和上面推导的方向相反,另外值得注意的是,在SimMechanicalcs中的 θ 2 \theta_2 θ2角度定义的参考系和上面的推导也不相同,它的角度是以下杆的方向为参考进行角度定义,也就是下杆和上杆之间的角度。因此为了和上面的公式推导结果相对比,在接入示波器之前将 θ 1 \theta_1 θ1和 θ 2 \theta_2 θ2加起来。如图所示,是使用SimMechanicalcs的仿真结果。
由图可见这个结果和上面动力学建模并使用Simulink仿真的结果完全相同,从而证明了之前动力学建模的正确性。
4.在平衡点附近模型线性化
系统在平衡点附近时, θ 1 \theta_1 θ1和 θ 2 \theta_2 θ2都很小,并且假设其角速度 θ 1 ˙ \dot{\theta_1} θ1˙和 θ 2 ˙ \dot{\theta_2} θ2˙也很小,则可进行近似处理: cos θ ≈ 1 , sin θ ≈ θ , sin θ θ ˙ ≈ 0 \cos{\theta} \approx 1, \sin\theta \approx \theta, \sin \theta \dot{\theta} \approx0 cosθ≈1,sinθ≈θ,sinθθ˙≈0。从而得到二阶倒立摆系统在平衡点附近的动力学方程为
[ M + m 1 + m 2 m 1 l 1 + m 2 L m 2 l 2 m 1 l 1 + m 2 L I 1 + m 1 l 1 2 + m 2 L 2 m 2 L l 2 m 2 l 2 m 2 L l 2 I 2 + m 2 l 2 2 ] [ x ¨ θ ¨ 1 θ ¨ 2 ] = [ 0 0 0 0 ( m 1 l 1 + m 2 L ) g 0 0 0 m 2 g l 2 ] [ x θ 1 θ 2 ] + [ 1 0 0 ] u \begin{aligned} \begin{array}{c} &\left[ \begin{array}{ccc} M+m_1+m_2 & m_1l_1+m_2L & m_2l_2 \\ m_1l_1+m_2L & I_1+m_1l_1^2+m_2L^2 & m_2Ll_2 \\ m_2l_2 & m_2Ll_2 & I_2+m_2l_2^2 \end{array}\right]\left[ \begin{array}{c} \ddot{x} \\ \ddot{\theta}_{1} \\ \ddot{\theta}_{2} \end{array}\right] &=\left[\begin{array}{ccc} 0 & 0 & 0 \\ 0 & (m_1l_1+m_2L)g & 0 \\ 0 & 0 & m_2gl_2 \end{array}\right]\left[ \begin{array}{c} x \\ \theta_{1} \\ \theta_{2} \end{array}\right]+\left[ \begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right]u \end{array}\end{aligned} ⎣⎡M+m1+m2m1l1+m2Lm2l2m1l1+m2LI1+m1l12+m2L2m2Ll2m2l2m2Ll2I2+m2l22⎦⎤⎣⎡x¨θ¨1θ¨2⎦⎤=⎣⎡0000(m1l1+m2L)g000m2gl2⎦⎤⎣⎡xθ1θ2⎦⎤+⎣⎡100⎦⎤u
使用MATLAB符号函数求逆的功能求解可得 [ x ¨ θ ¨ 1 θ ¨ 2 ] = [ a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 ] [ x θ 1 θ 2 ] + [ b 1 b 2 b 3 ] u \begin{aligned} \begin{array}{c} {\left[ \begin{array}{c} \ddot{x} \\ \ddot{\theta}_{1} \\ \ddot{\theta}_{2} \end{array} \right]= \left[ \begin{array}{ccc} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\\ \end{array} \right] \left[ \begin{array}{c} x \\ \theta_{1} \\ \theta_{2} \end{array} \right]+ \left[ \begin{array}{c} b_{1} \\ b_{2} \\ b_{3} \end{array} \right]u} \end{array}\end{aligned} ⎣⎡x¨θ¨1θ¨2⎦⎤=⎣⎡a11a21a31a12a22a32a13a23a33⎦⎤⎣⎡xθ1θ2⎦⎤+⎣⎡b1b2b3⎦⎤u
其中, a 11 = 0 a 12 = − I 2 g L 2 m 2 2 + g L l 1 l 2 2 m 1 m 2 2 + 2 I 2 g L l 1 m 1 m 2 + g l 1 2 l 2 2 m 1 2 m 2 + I 2 g l 1 2 m 1 2 I 1 I 2 M + I 1 I 2 m 1 + I 1 I 2 m 2 + I 2 L 2 M m 2 + I 2 M l 1 2 m 1 + I 1 M l 2 2 m 2 + I 2 L 2 m 1 m 2 + I 1 l 2 2 m 1 m 2 + I 2 l 1 2 m 1 m 2 + M l 1 2 l 2 2 m 1 m 2 − 2 I 2 L l 1 m 1 m 2 a 13 = − g m 1 l 1 2 l 2 2 m 2 2 − L g m 1 l 1 l 2 2 m 2 2 + I 1 g l 2 2 m 2 2 I 1 I 2 M + I 1 I 2 m 1 + I 1 I 2 m 2 + I 2 L 2 M m 2 + I 2 M l 1 2 m 1 + I 1 M l 2 2 m 2 + I 2 L 2 m 1 m 2 + I 1 l 2 2 m 1 m 2 + I 2 l 1 2 m 1 m 2 + M l 1 2 l 2 2 m 1 m 2 − 2 I 2 L l 1 m 1 m 2 a 21 = 0 a 22 = g ( I 2 L m 2 2 + I 2 l 1 m 1 2 + L M l 2 2 m 2 2 + I 2 L M m 2 + L l 2 2 m 1 m 2 2 + I 2 M l 1 m 1 + I 2 L m 1 m 2 + l 1 l 2 2 m 1 2 m 2 + I 2 l 1 m 1 m 2 + M l 1 l 2 2 m 1 m 2 ) I 1 I 2 M + I 1 I 2 m 1 + I 1 I 2 m 2 + I 2 L 2 M m 2 + I 2 M l 1 2 m 1 + I 1 M l 2 2 m 2 + I 2 L 2 m 1 m 2 + I 1 l 2 2 m 1 m 2 + I 2 l 1 2 m 1 m 2 + M l 1 2 l 2 2 m 1 m 2 − 2 I 2 L l 1 m 1 m 2 a 23 = − g l 2 2 m 2 2 ( L m 1 − l 1 m 1 + L M ) I 1 I 2 M + I 1 I 2 m 1 + I 1 I 2 m 2 + I 2 L 2 M m 2 + I 2 M l 1 2 m 1 + I 1 M l 2 2 m 2 + I 2 L 2 m 1 m 2 + I 1 l 2 2 m 1 m 2 + I 2 l 1 2 m 1 m 2 + M l 1 2 l 2 2 m 1 m 2 − 2 I 2 L l 1 m 1 m 2 a 31 = 0 a 32 = − g l 2 m 2 ( L 2 M m 2 − l 1 2 m 1 2 + L l 1 m 1 2 + L 2 m 1 m 2 + L M l 1 m 1 − L l 1 m 1 m 2 ) I 1 I 2 M + I 1 I 2 m 1 + I 1 I 2 m 2 + I 2 L 2 M m 2 + I 2 M l 1 2 m 1 + I 1 M l 2 2 m 2 + I 2 L 2 m 1 m 2 + I 1 l 2 2 m 1 m 2 + I 2 l 1 2 m 1 m 2 + M l 1 2 l 2 2 m 1 m 2 − 2 I 2 L l 1 m 1 m 2 a 33 = g l 2 m 2 ( I 1 m 1 + I 1 m 2 + I 1 M + l 1 2 m 1 m 2 + L 2 M m 2 + M l 1 2 m 1 + L 2 m 1 m 2 − 2 L l 1 m 1 m 2 ) I 1 I 2 M + I 1 I 2 m 1 + I 1 I 2 m 2 + I 2 L 2 M m 2 + I 2 M l 1 2 m 1 + I 1 M l 2 2 m 2 + I 2 L 2 m 1 m 2 + I 1 l 2 2 m 1 m 2 + I 2 l 1 2 m 1 m 2 + M l 1 2 l 2 2 m 1 m 2 − 2 I 2 L l 1 m 1 m 2 b 1 = I 2 m 2 L 2 + m 1 m 2 l 1 2 l 2 2 + I 2 m 1 l 1 2 + I 1 m 2 l 2 2 + I 1 I 2 I 1 I 2 M + I 1 I 2 m 1 + I 1 I 2 m 2 + I 2 L 2 M m 2 + I 2 M l 1 2 m 1 + I 1 M l 2 2 m 2 + I 2 L 2 m 1 m 2 + I 1 l 2 2 m 1 m 2 + I 2 l 1 2 m 1 m 2 + M l 1 2 l 2 2 m 1 m 2 − 2 I 2 L l 1 m 1 m 2 b 2 = − l 1 m 1 m 2 l 2 2 + I 2 L m 2 + I 2 l 1 m 1 I 1 I 2 M + I 1 I 2 m 1 + I 1 I 2 m 2 + I 2 L 2 M m 2 + I 2 M l 1 2 m 1 + I 1 M l 2 2 m 2 + I 2 L 2 m 1 m 2 + I 1 l 2 2 m 1 m 2 + I 2 l 1 2 m 1 m 2 + M l 1 2 l 2 2 m 1 m 2 − 2 I 2 L l 1 m 1 m 2 b 3 = − l 2 m 2 ( m 1 l 1 2 − L m 1 l 1 + I 1 ) I 1 I 2 M + I 1 I 2 m 1 + I 1 I 2 m 2 + I 2 L 2 M m 2 + I 2 M l 1 2 m 1 + I 1 M l 2 2 m 2 + I 2 L 2 m 1 m 2 + I 1 l 2 2 m 1 m 2 + I 2 l 1 2 m 1 m 2 + M l 1 2 l 2 2 m 1 m 2 − 2 I 2 L l 1 m 1 m 2 \begin{aligned} \begin{array}{l} a_{11}=0 \\ a_{12}= -\frac{I_2gL^2m_2^2 + gLl_1l_2^2m_1m_2^2 + 2I_2gLl_1m_1m_2 + gl_1^2l_2^2m_1^2m_2 + I_2gl_1^2m_1^2}{I_1I_2M + I_1I_2m_1 + I_1I_2m_2 + I_2L^2Mm_2 + I_2Ml_1^2m_1 + I_1Ml_2^2m_2 + I_2L^2m_1m_2 + I_1l_2^2m_1m_2 + I_2l_1^2m_1m_2 + Ml_1^2l_2^2m_1m_2 - 2I_2Ll_1m_1m_2} \\ a_{13}=-\frac{gm_1l_1^2l_2^2m_2^2 - Lgm_1l_1l_2^2m_2^2 + I_1gl_2^2m_2^2}{I_1I_2M + I_1I_2m_1 + I_1I_2m_2 + I_2L^2Mm_2 + I_2Ml_1^2m_1 + I_1Ml_2^2m_2 + I_2L^2m_1m_2 + I_1l_2^2m_1m_2 + I_2l_1^2m_1m_2 + Ml_1^2l_2^2m_1m_2 - 2I_2Ll_1m_1m_2}\\ a_{21}=0 \\ a_{22}=\frac{g(I_2Lm_2^2 + I_2l_1m_1^2 + LMl_2^2m_2^2 + I_2LMm_2 + Ll_2^2m_1m_2^2 + I_2Ml_1m_1 + I_2Lm_1m_2 + l_1l_2^2m_1^2m_2 + I_2l_1m_1m_2 + Ml_1l_2^2m_1m_2)}{I_1I_2M + I_1I_2m_1 + I_1I_2m_2 + I_2L^2Mm_2 + I_2Ml_1^2m_1 + I_1Ml_2^2m_2 + I_2L^2m_1m_2 + I_1l_2^2m_1m_2 + I_2l_1^2m_1m_2 + Ml_1^2l_2^2m_1m_2 - 2I_2Ll_1m_1m_2}\\ a_{23}=-\frac{gl_2^2m_2^2(Lm_1 - l_1m_1 + LM)}{I_1I_2M + I_1I_2m_1 + I_1I_2m_2 + I_2L^2Mm_2 + I_2Ml_1^2m_1 + I_1Ml_2^2m_2 + I_2L^2m_1m_2 + I_1l_2^2m_1m_2 + I_2l_1^2m_1m_2 + Ml_1^2l_2^2m_1m_2 - 2I_2Ll_1m_1m_2}\\ a_{31}=0 \\ a_{32}=-\frac{gl_2m_2(L^2Mm_2 - l_1^2m_1^2 + Ll_1m_1^2 + L^2m_1m_2 + LMl_1m_1 - Ll_1m_1m_2)}{I_1I_2M + I_1I_2m_1 + I_1I_2m_2 + I_2L^2Mm_2 + I_2Ml_1^2m_1 + I_1Ml_2^2m_2 + I_2L^2m_1m_2 + I_1l_2^2m_1m_2 + I_2l_1^2m_1m_2 + Ml_1^2l_2^2m_1m_2 - 2I_2Ll_1m_1m_2}\\ a_{33}=\frac{gl_2m_2(I_1m_1 + I_1m_2 + I_1M + l_1^2m_1m_2 + L^2Mm_2 + Ml_1^2m_1 + L^2m_1m_2 - 2Ll_1m_1m_2)}{I_1I_2M + I_1I_2m_1 + I_1I_2m_2 + I_2L^2Mm_2 + I_2Ml_1^2m_1 + I_1Ml_2^2m_2 + I_2L^2m_1m_2 + I_1l_2^2m_1m_2 + I_2l_1^2m_1m_2 + Ml_1^2l_2^2m_1m_2 - 2I_2Ll_1m_1m_2} \\ b_{1}=\frac{I_2m_2L^2 + m_1m_2l_1^2l_2^2 + I_2m_1l_1^2 + I_1m_2l_2^2 + I_1I_2}{I_1I_2M + I_1I_2m_1 + I_1I_2m_2 + I_2L^2Mm_2 + I_2Ml_1^2m_1 + I_1Ml_2^2m_2 + I_2L^2m_1m_2 + I_1l_2^2m_1m_2 + I_2l_1^2m_1m_2 + Ml_1^2l_2^2m_1m_2 - 2I_2Ll_1m_1m_2}\\ b_{2}=-\frac{ l_1m_1m_2l_2^2 + I_2Lm_2 + I_2l_1m_1}{I_1I_2M + I_1I_2m_1 + I_1I_2m_2 + I_2L^2Mm_2 + I_2Ml_1^2m_1 + I_1Ml_2^2m_2 + I_2L^2m_1m_2 + I_1l_2^2m_1m_2 + I_2l_1^2m_1m_2 + Ml_1^2l_2^2m_1m_2 - 2I_2Ll_1m_1m_2}\\ b_{3}=-\frac{l_2m_2(m_1l_1^2 - Lm_1l_1 + I_1)}{I_1I_2M + I_1I_2m_1 + I_1I_2m_2 + I_2L^2Mm_2 + I_2Ml_1^2m_1 + I_1Ml_2^2m_2 + I_2L^2m_1m_2 + I_1l_2^2m_1m_2 + I_2l_1^2m_1m_2 + Ml_1^2l_2^2m_1m_2 - 2I_2Ll_1m_1m_2} \end{array} \end{aligned} a11=0a12=−I1I2M+I1I2m1+I1I2m2+I2L2Mm2+I2Ml12m1+I1Ml22m2+I2L2m1m2+I1l22m1m2+I2l12m1m2+Ml12l22m1m2−2I2Ll1m1m2I2gL2m22+gLl1l22m1m22+2I2gLl1m1m2+gl12l22m12m2+I2gl12m12a13=−I1I2M+I1I2m1+I1I2m2+I2L2Mm2+I2Ml12m1+I1Ml22m2+I2L2m1m2+I1l22m1m2+I2l12m1m2+Ml12l22m1m2−2I2Ll1m1m2gm1l12l22m22−Lgm1l1l22m22+I1gl22m22a21=0a22=I1I2M+I1I2m1+I1I2m2+I2L2Mm2+I2Ml12m1+I1Ml22m2+I2L2m1m2+I1l22m1m2+I2l12m1m2+Ml12l22m1m2−2I2Ll1m1m2g(I2Lm22+I2l1m12+LMl22m22+I2LMm2+Ll22m1m22+I2Ml1m1+I2Lm1m2+l1l22m12m2+I2l1m1m2+Ml1l22m1m2)a23=−I1I2M+I1I2m1+I1I2m2+I2L2Mm2+I2Ml12m1+I1Ml22m2+I2L2m1m2+I1l22m1m2+I2l12m1m2+Ml12l22m1m2−2I2Ll1m1m2gl22m22(Lm1−l1m1+LM)a31=0a32=−I1I2M+I1I2m1+I1I2m2+I2L2Mm2+I2Ml12m1+I1Ml22m2+I2L2m1m2+I1l22m1m2+I2l12m1m2+Ml12l22m1m2−2I2Ll1m1m2gl2m2(L2Mm2−l12m12+Ll1m12+L2m1m2+LMl1m1−Ll1m1m2)a33=I1I2M+I1I2m1+I1I2m2+I2L2Mm2+I2Ml12m1+I1Ml22m2+I2L2m1m2+I1l22m1m2+I2l12m1m2+Ml12l22m1m2−2I2Ll1m1m2gl2m2(I1m1+I1m2+I1M+l12m1m2+L2Mm2+Ml12m1+L2m1m2−2Ll1m1m2)b1=I1I2M+I1I2m1+I1I2m2+I2L2Mm2+I2Ml12m1+I1Ml22m2+I2L2m1m2+I1l22m1m2+I2l12m1m2+Ml12l22m1m2−2I2Ll1m1m2I2m2L2+m1m2l12l22+I2m1l12+I1m2l22+I1I2b2=−I1I2M+I1I2m1+I1I2m2+I2L2Mm2+I2Ml12m1+I1Ml22m2+I2L2m1m2+I1l22m1m2+I2l12m1m2+Ml12l22m1m2−2I2Ll1m1m2l1m1m2l22+I2Lm2+I2l1m1b3=−I1I2M+I1I2m1+I1I2m2+I2L2Mm2+I2Ml12m1+I1Ml22m2+I2L2m1m2+I1l22m1m2+I2l12m1m2+Ml12l22m1m2−2I2Ll1m1m2l2m2(m1l12−Lm1l1+I1)
定义系统的状态变量为 ( x 1 , x 2 , x 3 , x 4 , x 5 , x 6 ) = ( x ˙ , θ 1 ˙ , θ 2 ˙ , x , θ 1 , θ 2 ) (x_1,x_2,x_3,x_4,x_5,x_6)=(\dot{x},\dot{\theta_1}, \dot{\theta_2},x, \theta_1,\theta_2) (x1,x2,x3,x4,x5,x6)=(x˙,θ1˙,θ2˙,x,θ1,θ2),系统的输入量为小车外力 u u u,系统输出为小车的位移 x x x,两个摆杆的角度 θ 1 , θ 2 \theta_1,\theta_2 θ1,θ2,则可得二阶倒立摆系统的状态空间方程为
[ x ¨ θ ¨ 1 θ ¨ 2 x ˙ θ ˙ 1 θ ˙ 2 ] = [ 0 0 0 a 11 a 12 a 13 0 0 0 a 21 a 22 a 23 0 0 0 a 31 a 32 a 33 1 0 0