知识图谱——TransE模型原理
知识图谱——TransE模型原理
1 TransE模型介绍
1.1 TransE模型引入
在我们之前的文章中,提到了知识图谱补全任务的前提任务是知识表示学习,在知识表示学习中,最为经典的模型就是TransE模型,TransE模型的核心作用就是将知识图谱中的三元组翻译成embedding向量。
1.2 TransE模型思想
为了后面便于表示,我们先设定一些符号
- h 表示知识图谱中的头实体的向量。
- t 表示知识图谱中的尾实体的向量。
- r 表示知识图谱中的关系的向量。
在TransE模型中,有这样一个假设:
t = h + r t=h+r t=h+r
也就是说,正常情况下的尾实体向量=头实体向量+关系向量。用图的方式描述如下:
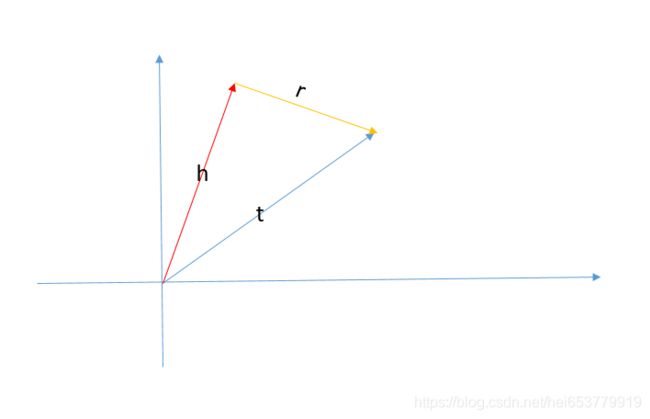
如果一个三元组不满足上述的的关系,我们就可以认为这是一个错误的三元组。
1.3 TransE模型的目标函数
首先,我们先来介绍两个数学概念:
L1范数
也称为曼哈顿距离,对于一个向量X而言,其L1范数的计算公式为:
∣ ∣ X ∣ ∣ L 1 = ∑ i = 1 n ∣ x i ∣ ||X||_{L1}=∑_{i=1}^n|x_i| ∣∣X∣∣L1=i=1∑n∣xi∣
其中, x i x_i xi表示向量X的第i个属性值,这里我们取的是绝对值。并且,使用L1范数可以衡量两个向量之间的差异性,也就是两个向量的距离。
D i s t a n c e L 1 ( X 1 , X 2 ) = ∑ i = 1 n ∣ X 1 i − X 2 i ∣ Distance_{L1}(X_1,X_2)=∑_{i=1}^n|X_{1i}-X_{2i}| DistanceL1(X1,X2)=i=1∑n∣X1i−X2i∣
L2范数
也称为欧式距离,对于一个向量X而言,其L2范数的计算公式为:
∣ ∣ X ∣ ∣ L 2 = ∑ i = 1 n X i 2 ||X||_{L2}=\sqrt{∑_{i=1}^nX_i^2} ∣∣X∣∣L2=i=1∑nXi2
同样,L2范数也可以用来衡量两个向量之间的差距:
D i s t a n c e L 2 ( X 1 , X 2 ) = ∑ i = 1 n ( X 1 i − X 2 i ) 2 Distance_{L2}(X_1,X_2)=∑_{i=1}^n(X_{1i}-X_{2i})^2 DistanceL2(X1,X2)=i=1∑n(X1i−X2i)2
根据我们上面介绍的Trans中的假设,我们可以知道,对于一个三元组而言,头实体向量和关系向量之和与尾实体向量越接近,那么说明该三元组越接近一个正确的三元组,差距越大,那么说明这个三元组越不正常。那么我们可以选择L1或者L2范数来衡量三个向量的差距。而我们的目标就是使得争取的三元组的距离越小越好,错误的三元组距离越大越好,也就是其相反数越小越好。数学化的表示就是:
m i n ∑ ( h , r , t ) ∈ G ∑ ( h ′ , r ′ , t ′ ) ∈ G ′ [ γ + d i s t a n c e ( h + r , t ) − d i s t a n c e ( h ′ + r ′ , t ′ ) ] + min∑_{(h,r,t)∈G}∑_{(h',r',t')∈G'}[γ+distance(h+r,t)-distance(h'+r',t')]_+ min(h,r,t)∈G∑(h′,r′,t′)∈G′∑[γ+distance(h+r,t)−distance(h′+r′,t′)]+
其中:
( h , r , t ) (h,r,t) (h,r,t):表示正确的三元组
( h ′ , r ′ , t ′ ) (h',r',t') (h′,r′,t′): 表示错误的三三元组
γ γ γ :表示正样本和负样本之间的间距,一个常数
[ x ] + [x]_+ [x]+:表示max(0,x)
我们来简单的解释以下目标函数,我们的目标是让正例的距离最小,也就是 m i n ( d i s t a n c e ( h + r , t ) ) min(distance(h+r,t)) min(distance(h+r,t)),让负例的相反数最小也就是 ( m i n ( − d i s t a n c e ( h ′ + r ′ , t ′ ) ) ) (min(-distance(h'+r',t'))) (min(−distance(h′+r′,t′))),对于每一个正样本和负样本求和,再增加一个常数的间距,就是整体距离的最小值。也就是我们的目标函数。
1.4 目标函数的数学推导
这里,我们采用欧氏距离作为distance函数,则目标函数可以改写为:
m i n ∑ ( h , r , t ) ∈ G ∑ ( h ′ , r ′ , t ′ ) ∈ G ′ [ γ + ( h + r − t ) 2 − ( h ′ + r ′ − t ′ ) 2 ] + min∑_{(h,r,t)∈G}∑_{(h',r',t')∈G'}[γ+(h+r-t)^2-(h'+r'-t')^2]_+ min(h,r,t)∈G∑(h′,r′,t′)∈G′∑[γ+(h+r−t)2−(h′+r′−t′)2]+
则对于损失函数loss就有:
L o s s = ∑ ( h , r , t ) ∈ G ∑ ( h ′ , r ′ , t ′ ) ∈ G ′ [ γ + ( h + r − t ) 2 − ( h ′ + r − t ′ ) 2 ] + Loss = ∑_{(h,r,t)∈G}∑_{(h',r',t')∈G'}[γ+(h+r-t)^2-(h'+r-t')^2]_+ Loss=(h,r,t)∈G∑(h′,r′,t′)∈G′∑[γ+(h+r−t)2−(h′+r−t′)2]+
在损失函数中,我们知道所有的参数包括{ h , r , t , h ′ , r , t ′ h,r,t,h',r,t' h,r,t,h′,r,t′}。下面,我们来逐个进行梯度推导:
- 首先是对h的梯度,对于某一个 h i h_i hi而言
∂ L o s s ∂ h i = ∑ ( h , r , t ) ∈ G ∑ ( h ′ , r , t ′ ) ∈ G ′ ∂ [ γ + ( h + r − t ) 2 − ( h ′ + r − t ′ ) 2 ] + ∂ h i \frac{∂Loss}{∂h_i}= ∑_{(h_,r,t)∈G}∑_{(h',r,t')∈G'}\frac{∂[γ+(h+r-t)^2-(h'+r-t')^2]_+}{∂h_i} ∂hi∂Loss=(h,r,t)∈G∑(h′,r,t′)∈G′∑∂hi∂[γ+(h+r−t)2−(h′+r−t′)2]+
在整个求和的过程中,只针对包含 h i h_i hi的项求导:
∂ [ γ + ( h i + r − t ) 2 − ( h ′ + r − t ′ ) 2 ] + ∂ h i \frac{∂[γ+(h_i+r-t)^2-(h'+r-t')^2]_+}{∂h_i} ∂hi∂[γ+(hi+r−t)2−(h′+r−t′)2]+
有:
∂ [ γ + ( h i + r − t ) 2 − ( h ′ + r − t ′ ) 2 ] + ∂ h i = { 2 ( h i + r − t ) γ + ( h + r − t ) 2 − ( h ′ + r − t ′ ) 2 > 0 0 γ + ( h + r − t ) 2 − ( h ′ + r − t ′ ) 2 < = 0 \frac{∂[γ+(h_i+r-t)^2-(h'+r-t')^2]_+}{∂h_i}= \begin{cases} 2(h_i+r-t)&&γ+(h+r-t)^2-(h'+r-t')^2>0\\ 0 &&γ+(h+r-t)^2-(h'+r-t')^2<=0 \end{cases} ∂hi∂[γ+(hi+r−t)2−(h′+r−t′)2]+={2(hi+r−t)0γ+(h+r−t)2−(h′+r−t′)2>0γ+(h+r−t)2−(h′+r−t′)2<=0
则原式变为:
∂ L o s s ∂ h i = ∑ ( h i , r , t ) ∈ G ∑ ( h ′ , r , t ′ ) ∈ G ′ { 2 ( h i + r − t ) γ + ( h i + r − t ) 2 − ( h ′ + r − t ′ ) 2 > 0 0 γ + ( h i + r − t ) 2 − ( h ′ + r − t ′ ) 2 < = 0 \frac{∂Loss}{∂h_i}= ∑_{(h_i,r,t)∈G}∑_{(h',r,t')∈G'} \begin{cases} 2(h_i+r-t)&&γ+(h_i+r-t)^2-(h'+r-t')^2>0\\ 0 &&γ+(h_i+r-t)^2-(h'+r-t')^2<=0 \end{cases} ∂hi∂Loss=(hi,r,t)∈G∑(h′,r,t′)∈G′∑{2(hi+r−t)0γ+(hi+r−t)2−(h′+r−t′)2>0γ+(hi+r−t)2−(h′+r−t′)2<=0
同理对于 t i , h i ′ , t i ′ t_i,h_i',t_i' ti,hi′,ti′有:
∂ L o s s ∂ t i = ∑ ( h , r , t i ) ∈ G ∑ ( h ′ , r , t ′ ) ∈ G ′ { − 2 ( h + r − t i ) γ + ( h + r − t i ) 2 − ( h ′ + r − t ′ ) 2 > 0 0 γ + ( h + r − t i ) 2 − ( h ′ + r − t ′ ) 2 < = 0 \frac{∂Loss}{∂t_i}= ∑_{(h,r,t_i)∈G}∑_{(h',r,t')∈G'} \begin{cases} -2(h+r-t_i)&&γ+(h+r-t_i)^2-(h'+r-t')^2>0\\ 0 &&γ+(h+r-t_i)^2-(h'+r-t')^2<=0 \end{cases} ∂ti∂Loss=(h,r,ti)∈G∑(h′,r,t′)∈G′∑{−2(h+r−ti)0γ+(h+r−ti)2−(h′+r−t′)2>0γ+(h+r−ti)2−(h′+r−t′)2<=0
∂ L o s s ∂ h i ′ = ∑ ( h , r , t ) ∈ G ∑ ( h i ′ , r , t ′ ) ∈ G ′ { − 2 ( h ′ + r − t ′ ) γ + ( h + r − t ) 2 − ( h i ′ + r − t ′ ) 2 > 0 0 γ + ( h + r − t ) 2 − ( h i ′ + r − t ′ ) 2 < = 0 \frac{∂Loss}{∂h_i'}= ∑_{(h,r,t)∈G}∑_{(h_i',r,t')∈G'} \begin{cases} -2(h'+r-t')&&γ+(h+r-t)^2-(h_i'+r-t')^2>0\\ 0 &&γ+(h+r-t)^2-(h_i'+r-t')^2<=0 \end{cases} ∂hi′∂Loss=(h,r,t)∈G∑(hi′,r,t′)∈G′∑{−2(h′+r−t′)0γ+(h+r−t)2−(hi′+r−t′)2>0γ+(h+r−t)2−(hi′+r−t′)2<=0
∂ L o s s ∂ t i ′ = ∑ ( h , r , t ) ∈ G ∑ ( h ′ , r , t i ′ ) ∈ G ′ { 2 ( h ′ + r − t ′ ) γ + ( h + r − t ) 2 − ( h ′ + r − t i ′ ) 2 > 0 0 γ + ( h + r − t ) 2 − ( h ′ + r − t i ′ ) 2 < = 0 \frac{∂Loss}{∂t_i'}= ∑_{(h,r,t)∈G}∑_{(h',r,t_i')∈G'} \begin{cases} 2(h'+r-t')&&γ+(h+r-t)^2-(h'+r-t_i')^2>0\\ 0 &&γ+(h+r-t)^2-(h'+r-t_i')^2<=0 \end{cases} ∂ti′∂Loss=(h,r,t)∈G∑(h′,r,ti′)∈G′∑{2(h′+r−t′)0γ+(h+r−t)2−(h′+r−ti′)2>0γ+(h+r−t)2−(h′+r−ti′)2<=0
最后对于 r i r_i ri,γ有:
∂ L o s s ∂ r i = ∑ ( h , r i , t ) ∈ G ∑ ( h ′ , r i , t ′ ) ∈ G ′ { 2 ( h + r i − t ) − 2 ( h ′ + r i − t ′ ) γ + ( h + r i − t ) 2 − ( h ′ + r i − t ′ ) 2 > 0 0 γ + ( h + r i − t ) 2 − ( h ′ + r i − t ′ ) 2 < = 0 \frac{∂Loss}{∂r_i}=∑_{(h,r_i,t)∈G}∑_{(h',r_i,t')∈G'} \begin{cases} 2(h+r_i-t)-2(h'+r_i-t')&&γ+(h+r_i-t)^2-(h'+r_i-t')^2>0\\ 0 &&γ+(h+r_i-t)^2-(h'+r_i-t')^2<=0 \end{cases} ∂ri∂Loss=(h,ri,t)∈G∑(h′,ri,t′)∈G′∑{2(h+ri−t)−2(h′+ri−t′)0γ+(h+ri−t)2−(h′+ri−t′)2>0γ+(h+ri−t)2−(h′+ri−t′)2<=0
∂ L o s s ∂ γ = ∑ ( h , r , t ) ∈ G ∑ ( h ′ , r ′ , t ′ ) ∈ G ′ { 1 γ + ( h + r − t ) 2 − ( h ′ + r − t ′ ) 2 > 0 0 γ + ( h + r − t ) 2 − ( h ′ + r − t ′ ) 2 < = 0 \frac{∂Loss}{∂γ}= ∑_{(h,r,t)∈G}∑_{(h',r',t')∈G'} \begin{cases} 1&&γ+(h+r-t)^2-(h'+r-t')^2>0\\ 0 &&γ+(h+r-t)^2-(h'+r-t')^2<=0 \end{cases} ∂γ∂Loss=(h,r,t)∈G∑(h′,r′,t′)∈G′∑{10γ+(h+r−t)2−(h′+r−t′)2>0γ+(h+r−t)2−(h′+r−t′)2<=0
1.5 如何产生负样本
在我们之前算法描述中,我们提到了负样本的问题,对于一个知识图谱而言,其中保存的全部都是正样本时肯定的了。那么,我们应该如何获取负样本呢?
具体的可以通过随机替换头实体的方式来实现一个错误的三元组,或者采用随机替换一个错误的尾实体的方式来形成一个错误的三元组。
同时,为了避免,我们在替换形成的三元组也存在于知识图谱中,我们需要在替换之后进行过滤。
2 参考文章
- TransE如何进行向量更新?
- TransE算法详解