复盘：手推SVM支持向量机二分类超平面，求解目标函数原问题，kkt条件，对偶问题求q，核函数、hinge loss损失函数，硬间隔，软间隔，最后得到w和b

复盘：手推SVM支持向量机二分类超平面，求解目标函数原问题，kkt条件，对偶问题求q，核函数、hinge loss损失函数，硬间隔，软间隔，最后得到w和b

提示：系列被面试官问的问题，我自己当时不会，所以下来自己复盘一下，认真学习和总结，以应对未来更多的可能性

关于互联网大厂的笔试面试，都是需要细心准备的
（1）自己的科研经历，科研内容，学习的相关领域知识，要熟悉熟透了
（2）自己的实习经历，做了什么内容，学习的领域知识，要熟悉熟透了
（3）除了科研，实习之外，平时自己关注的前沿知识，也不要落下，仔细了解，面试官很在乎你是否喜欢追进新科技，跟进创新概念和技术
（4）准备数据结构与算法，有笔试的大厂，第一关就是手撕代码做算法题
面试中，实际上，你准备数据结构与算法时以备不时之需，有足够的信心面对面试官可能问的算法题，很多情况下你的科研经历和实习经历足够跟面试官聊了，就不需要考你算法了。但很多大厂就会面试问你算法题，因此不论为了笔试面试，数据结构与算法必须熟悉熟透了
秋招提前批好多大厂不考笔试，直接面试，能否免笔试去面试，那就看你简历实力有多强了。

---

面试官：你了解SVM吗？手动推导一下svm超平面要求解的目标函数

谈一个复杂但十分有趣的话题，
支持向量机the support vector machine。

今天的节目将专注于帮助大家从直觉上更好的理解SVM模型。

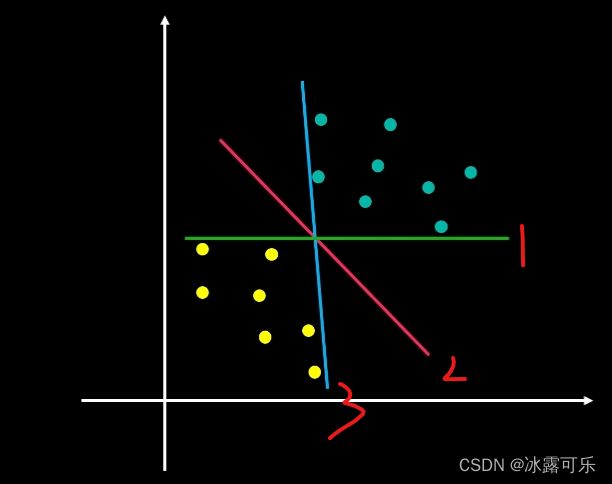
首先来看下面的问题，在这个二维的空间里存在着这些数据点，不同的颜色代表着两种不同的数据类别。

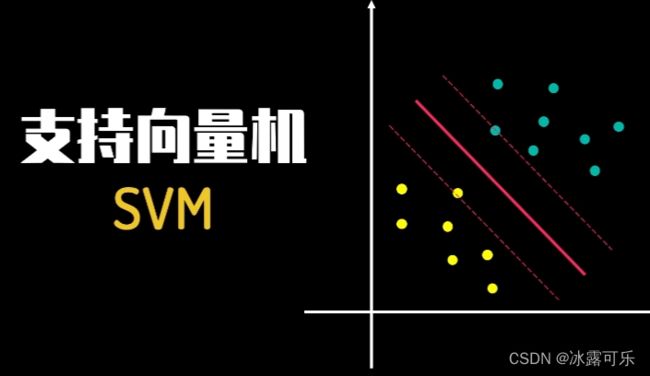
如果我需要你画一条直线，能将两类数据区分开来，
并且当有新数据加入时，根据这条线，我们也能够判别它属于哪一类，

那么你会怎么画这条线呢？

是上面这样画，

这样画还是这样画？1 2 3三种线条

这个问题可以进一步延伸到三维空间中，
我们如何让一个二维平面区分两类数据，
也可以再进一步推演到四维空间，
如何让三维超平面区分两类数据，以此类推，那么以上这类问题就可以被归纳为为了去。

区分2类维度数据，

两类维度数据，N维数据的样本数M为维度数，
如何设计一个维度为M减一的超平面，将两类数据区分开来，

W可以理解为X对应的权重。

为了便于我们直觉理解，以下我会先以二维空间的问题为例，

找到那条分割线决策边界，Decision boundary，

我们先看第一种画法，看看它存在什么样的问题。

两类数据都有相应的数据点，与决策边界线非常接近，这种画法很危险的。
当我们有一个新的数据同样接近于该直线时，这样分类错误的概率是非常大的。

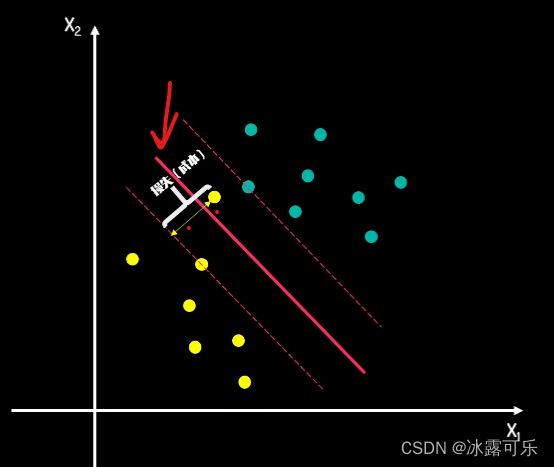
我们再看另一种画法，在这种画法中，
两类数据中所有的点都与决策边界线保持了一定的距离，这个距离起到了缓冲区的作用。

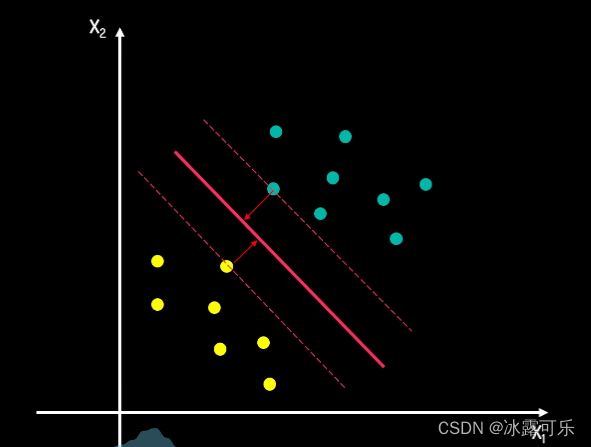
当这个缓冲区足够大时，分类结果的可信度就更高了。
我们把这个缓冲区称为间隔margin，这个间隔把两类数据所处的空间分隔开来，

间隔距离可以体现出两类数据的差异大小，越大的间隔意味着两类数据差异越大，那么我们区分起来就越容易。

因此，寻找最佳决策边界线的问题可以转化为
求解两类数据的最大间隔问题，
而间隔的正中就是我们的决策边界。

当有新数据需要判断时，根据它处于决策边界的相对位置，
我们就可以进行分类了，假设决策边界的超平面方程式为

它上下分别移动C来到对应的间隔上下边界。

由于上下边界一定会经过一些样本数据点，而这些点距离决策边界最近，
它们决定了间隔距离，我们称它们为支持向量support vector。

这也是为什么，我们将该方法命名为支持向量基support vector machine。

——这就是svm命名的来源

我们把等式两边分别除以C得到，我们可以用W撇一，W撇2，B撇分别也替换原方程变量，得到新方程，

方程式右侧被转化为正负一，这样我们就可以将上述两个方程式定义为正负超平面。

由于W撇B撇只是我们需要求解的代号，把它们替换成WB
也不影响计算所以最终只需要求解WB
得到下面三个超平面方程式，

正超平面
决策超平面
负超平面，

所有正超平面及其上方的数据点颜色相同都属于正类，负超平面及其下方的点为负类。

当有新数据加入需要我们分类判断时，
我们则，可以利用它与决策超平面的相对位置来进行分类。

关于如何对WB进行求解，
我们下面一会深入探讨svm背后的数学推导。

假如我们的初始数据发生了如下的变化，下面黄点异常了

根据之前的方法，最后间隔会是，

如果我们忽略中间的这个异常点，那么间隔距离也会明显增加，

那么我们需不需要为这样一个异常值而牺牲我们的间隔距离？
当有更多的异常值？

所以我们可以引入损失因子这个概念，

那些违背规则的异常点都会有对应的损失值。
你可以把间隔距离想象成经营收入，而损失值想象成经营成本，
我们的目标则转化为同时考虑收入和成本因素去最大化我们的利润。

这个对应底下形成的间隔，我们称之为软间隔soft margin，
它有一定的容错率，目的是在间隔距离和错误大小之间找到一个平衡，

而之前推导出的间隔则被称为硬间隔hard margin。

关于软间隔，我们会在后面专门的间隔进行探讨。

升维转换和ctrator和技巧：

在了解和技巧之前，我们首先需要了解什么是升维转换。
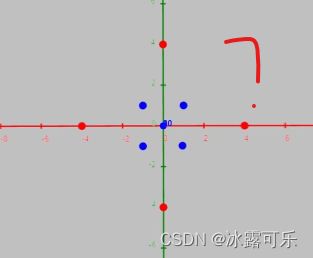
看下面的例子，在这个二维空间中。

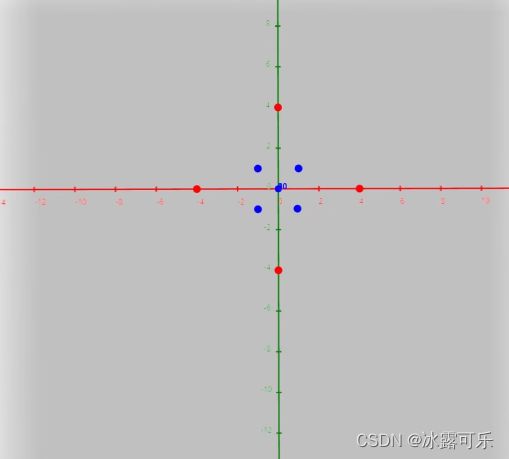
很显然，我们不能通过一条直线将其有效区分，

但如果我们进行下面的升维转换，增加一个新维度的话，

就可以在这个三维空间中，通过超平面将数据区分了。

那么对于这些在低维度下无法方便分类的数据，
我们就可以采用类似的方法，

一、通过合适的维度，转换函数将低维数据进行升维，

二、在高维度下求解FBI模型，找到对应的分割超平面。

当有新数据需要进行分类预测时，可以对其先做升维转换操作。
再根据高维度下的角色边界，超平面进行判断，

不过提升维度，你需要明确的维度，转换函数以及更多的数据存储计算需求。
那么，有没有一种方法能够避免将数据送入高维度进行计算，

却又能获得同样的分类效果？

那么我们就需要运用kernel trick核技巧了。
由于SBM的本质是量化两类数据差异的方法，而和函数克隆方向能够提供高维度向量相似度的测量，

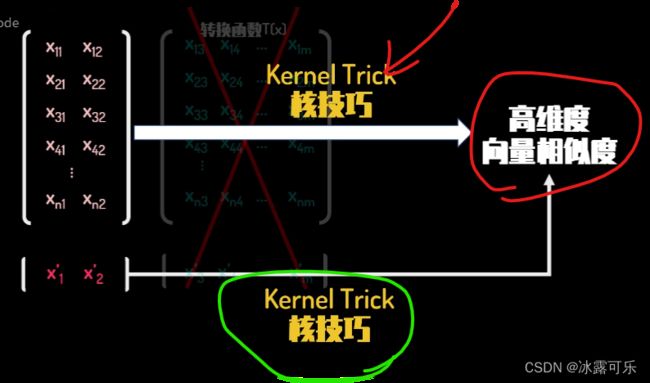
通过选取合适的和公式，我们就可以不用知晓具体的维度转化函数
直接获得数据的高维度差异度，并以此来进行分类判断。

我们下面会专门探讨和技巧，这需要基于我们后面SVM数学推导中的一些知识点，
这里我就先点到为止，

---

顺着直觉来求解svm超平面的w和b

这节不可避免的会使用到一些中高阶的数学知识，比如向量计算、拉格朗、日程、字法、梯度优化等概念，

不过我也会尝试用通俗易懂的可视化例子解释他们背后的核心思想。
那么让我们进入正题，

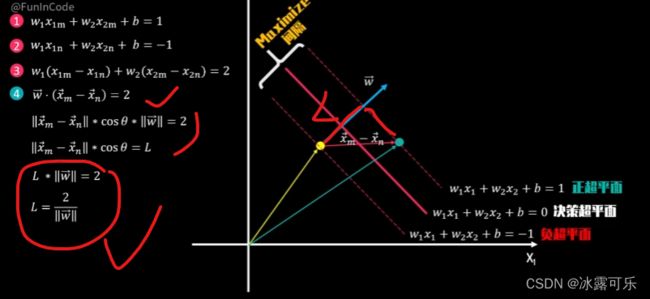
还是先以二维数据为例，我们的目标是最大化正负超平面间的间隔距离L，
那么构建L的表达式就非常重要了。

我们分别在正负超平面上随机选取一个支持向量点Xn和xm，
为了清晰展示，我们把其余点引去，
由于它们都位于正负超平面上，所以满足超平面等式一二

我们将等式一减去等式二得到等式=等式三
可以理解为向量W和向量XM减XN的点击结果为二，其中向量XN减XM，我们在图中已经展示出来了。

接下来，我们看向量W在决策超平面上随机选择两个点op，
它们满足等式五六，我们用等式五减六得到等式七，
它可以被理解为向量W和向量xo减XP的点击结果为零，

因为向量的点击结果为两个向量的长度相乘，再乘以它们之间的夹角cos值
当点击结果为零时，意味着两向量夹角为90度两个向量垂直。
所以点击结果可以反映出向量的相似性。

当点击结果为正时，两者的方向具有相似性。

当点击结果为零两向量垂直
点击为负时两向量方向背离

根据的是八本例中向量W和向量xo减XP垂直。
由于向量xo减XP就处于决策边界上，
因此我们可以得到向量W与决策超平面垂直。

现在再回到本式四，

我们已知向量W与决策超平面垂直向量XM减XN与之的点击，
结果就可以等加于向量XM减N的长度乘以向量W的长度，
再乘以两者的夹角cos西塔而向量XM减XN的长度乘以夹角Cos贝塔
为向量XM减SN投影到向量W上的强度，

也就是我们要求的正负超平面间隔距离L，

我们最后可以得到间隔距离L的表达式，
由于我们需要最大化L，这等同于求解，
在约束条件下向量W长度的最小化问题。

我们现在来看约束条件
所有绿色点都属于正类，对应的分类值Y等于一。

就因为它们处于正常平面上，都位于其上方，
所以向量W与向量Xi的点击，结果加B大于等于一，

同样的所有红点属于负类。对应分类值Y等于负一，
满足约束条件向量W与向量Xi的点击，结果加B小于等于负一。

从以上约束条件中，我们可以归纳出下面的2点：
一，约束表达式均为反射函数约束，
二，约束表达式可以进一步提炼为Yi乘以向量，W与向量Xi的点击，结果加B的和大于等于一，

【是不是很像LR里面的p(y|x)=f的yi次方 * (1-f)的(1-yi)次方，实际上就是一个二分类问题，这里svm而已】

那么最后的优化问题可以总结为，

其中向量W的长度为向量W的L2范数
W1的平方加上W2的平方再开根号。
为了把根号去除并优化未来计算，我们可以对目标表达式先平方，再除二
得到最终的目标优化问题。

很显然，这是一个在仿射函数约束下的凸优化问题，

我们知道如果约束条件是等式的话，我们可以直接使用拉格朗日乘子法求解，
但如果约束条件是不等式的话，我们需要进行一些变化，
通过增加一个非负变量pi的平方，将不等式转化为等式约束，再使用拉格朗日乘子法。

所以我们就有了下面的拉格朗日方程式。

拉格朗日乘子法求解w，b，lambda

为了求上述方程式的极值，我们对W，B，lamadai， pi分别求偏等极值均为零，
得到

我们把等式四左右两边分别除以二再乘pi得到
lambdai乘以pi的平方等于零，

将约束条件三带入等式四，得到新的等式四。

这就很有意思了，
根据约束条件括号内的值非负，
那么满足新等式四成立只有两种可能性，
一：括号内的值大于零，这意味着对应数据点不在正负超平面上，此时lambdai必须等于零。

二：括号内的值等于零，此时lambdai可以不为零。

我们可以把拉格朗日乘子lambdai看作违背约束条件的乘法系数。

根据上述推导，当不满足约束条件时，括号内的值小于零，
此时，如果拉格朗日方程式的后半部分会小于零，
这会让最终的拉格朗日方程式的值变得更小，
这相当于变相去鼓励违反约束

而获得更小直解，这是违反常理的，

因此。从直觉上判断，我们可以推断出lambdai大于等于零，
因此。从直觉上判断，我们可以推断出lambdai大于等于零，
因此。从直觉上判断，我们可以推断出lambdai大于等于零，

我们也可以借助下面的几何可视化
来帮助理解lambdai非负这一条件。

我们的目标是在约束条件下，求FW的最小值。
由于我们当前以二为空间为例，W1W2可以看作横纵坐标
FW在W1W2坐标系下的等高线图如下

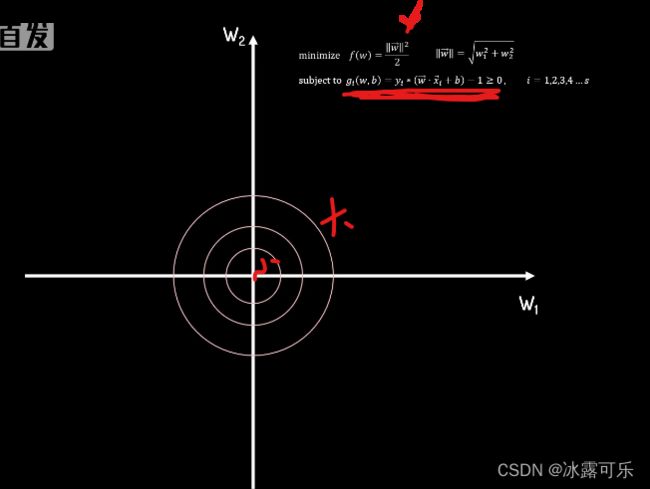
每个圆圈上的W1W2组合都有相同的FW值，越靠近圆心FW值越小。

在没有约束的条件下，很显然最小值会在圆点处得到，

但只有一个约束条件，即一大于等于零时。

可行区域用绿色表示，很显然，最小值会在等高线圆与约束边界线相切处得到。

此时，在切点处，FW的梯度向量倒三角f
指向其函数值增加最大的方向。如图中的红色箭头所示，

而约束条件第一的梯度向量，倒三角g1方向也指向其函数值，增加最大的方向，
用绿色箭头表示其约束分界线方向垂直。

很显然两个梯度向量方向一致，而大小可以通过一个大于零的lambda1调整至相同。

当第二个约束条件G2加入后，两约束边界的相交点为最优解，此时FW在最优解处的。

梯度向量方向在两约束边界梯度向量包夹的区域内，

因此可以由G1，G2的梯度向量分别乘以大于零的调整系数lambda1和lambda2后
相加组合而成。

当第三个约束条件G3加入后，最优解已经有约束条件一二在他们的约束边界交点数所决定，
此时最优解向量W星不在G3约束边界线上，
此时G3大于零约束条件不起实质作用，lambda3等于零

综合以上简单的可数化分析，我们也可以更直观的理解lambdai大于等于零，这一条件了，

那么最后我们就有了下面五个条件，也就是之前提到的KKT条件了，

基于KKT条件就可以求解最终的决策超平面了。

---

求解svm原问题的对偶问题，方便求解

不过在SVM模型中，为了求解的效率和更方便的应用符合技巧，kernel trick，
我们往往会将原问题转化为其自身的对偶问题，再求解

这就是我们接下来要谈的SVM对偶性，

这是我们的原问题，

在gi大于等于零的约束条件下，去最小化SW它的最优解，
满足KKT条件在向量W星和B星处求得

现在我们设立新的方程式q lambdai，

由于最小化minimize符号的存在，下面的不等式必然成立。

根据之前的KKT条件，lambdai大于等于0。GI大于等于零，
所以FW星减一个非负数一定小于或等于自身，

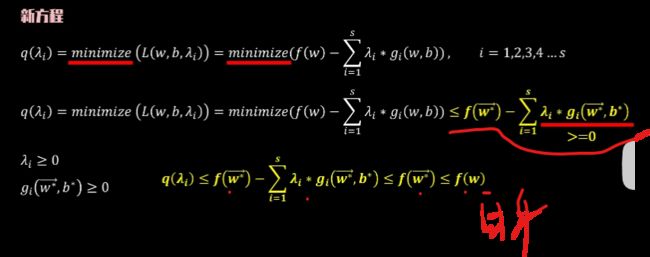
同时FW星是我们的极小之解，
所以我们有Q lambdai小于等于FW星，小于等于FW，

可以看到Q lambdai为FW的下界。

那么我们可以去寻找一个最优下界Qlambdai星，
让Qlambdai星与FW星尽可能的接近。

所以我们会有QQlambdai小于等于Qlambdai星，小于等于FW星，小于等于FW。

这里寻找最优Qlambdai星等同于求解下面的最优化问题，

在满足M的I大于等于零的约束条件下，去求解最大化的Qlambdai的解，
这就是SVM原问题的对偶问题，

Qlambdai星，小于FW性时，我们称之为弱对偶，
假如中间等号成立，Qlambdai星等于FW星。
大小差异消失，我们称之为强对偶。

当强对偶成立时，我们就可以通过求解对偶问题，同时得到原问题的解。

当满足某些特定条件，比如在当前仿射函数约束下，求解图优化问题时，强对偶成立。

而且我们可以证明，当Qlambdai星等于FW星时，两者同时得到最优解，

证明；

现在我用一个更简单的函数可视化例子，帮助大家加深对上面概念的理解。

假设我们要求解下面的原问题，

FX等于X平方的最小值
满足约束条件X减一大于等于零。

原问题是，只有单反射约束条件的不优化问题，它的最优解非常直观，当X等于一时。
FX等于一为FX在约束条件下的极值解，【上面黄色点】

为了验证它的对偶性性，我们构建q lambda，

满足约束条件lambda大于等于零，
根据KKT条件q lambda对X求偏的取值为零，得到X等于二分之lambda，

将其带回原方程，得到q lambda等于负四分之lambda平方再加lambda。

当我们调整lambda，我们可以清楚的看到哪个朗日方程式
X平方减Lambda乘以X减一的变化，
也能够看到它的最小值q lambda的变化趋势。

我们把不同lambda下的拉格朗日方程的最小值轨迹画出来，就得到了图中的曲线，

这个最小值轨迹落在原问题的极值下方，
说明q lambda是原问题的下界。

为了找到那个最优的下界，我们对q lambda求最大值
得到当lambda等于二。
x等于一时
q lambda最大的值为一

这个极值解与原问题FX在X等于一时取得的极值解相同
强对偶成立。

所以我们可以通过求解原问题的对偶问题解决原问题。

很多时候对偶问题求解起来更方便，并且能够表现出一些非常有用的特征。

了解这些就需要回到我们之前更复杂的SVM对偶问题的求解例子中了，

先对最小化部分求解，我们可以直接套入之前的KKT条件

结果得到更精简的优化方程，求解lambdai后就可以求解得到W向量。

而我们又知道，根据KKT条件，
只有正负超平面上的支持向量lambdai值大于零，
其余向量点lambdai值为零
零与任何数相乘得零，不影响W向量的结果。

所以我们在计算W向量的过程中，只需要用到支持向量，计算量显著减少

完成向量W的计算后，我们再将向量W和正负超平面上的支持向量Xi
套回正负超平面方程就可以求得B了。

之所以我们绕了这样一大圈去求解对偶问题，
除了对偶问题从表达式和约束条件上更简洁以外，
更主要的原因是因为对偶问题有一个非常好的特征，

也就是最优解仅根据支持向量的点击结果所决定，
也就是最优解仅根据支持向量的点击结果所决定，
也就是最优解仅根据支持向量的点击结果所决定，

也可以理解为仅优支持向量的空间相似度所决定，

这就为我们下面将的kernel trick铺平了道路，

既然我们只需要利用空间相似度结果，
而这直接就可以通过核函数求得，

那为什么还需要绕一圈去寻找维度转化函数了？下面我来说

到这里，你能看完的，说明你已经很牛逼了，为学习SVM打下了坚实的基础！
到这里，你能看完的，说明你已经很牛逼了，为学习SVM打下了坚实的基础！
到这里，你能看完的，说明你已经很牛逼了，为学习SVM打下了坚实的基础！

---

维度转换函数T到核函数

之前我们说了，二维没法区分，

就要通过维度转换函数TX，
我们可以把原维度进行变换，得到新的维度，
数据向量TX原优化问题，经过深维也随之转换为下面的形式。

当遇到非线性分类问题时，原维度下决策超平面无解，
此时通过维度转换函数TX将原维度数据进行深维转换，
我们就可以在新维度空间中求解决策，超平面以上便是核技巧的概念基础。

另外，在上面中我们介绍了SVM原问题的对偶问题，

在M的I大于等于零的约束条件下，求解函数Q的最大值
其最优解在lambdai星处取得，有了lambdai星，决策超平面的参数WB便迎刃而解。
而这个最优解，lambdai星取决于下面的值数据

一，每个数据点的正负标签Y值
二，数据点向量之间的量量点击结果

回到最初的非线性分类SVM问题是，以上目标方程在原维度下无解。

我们将x升维T(x)转化

那么如何得到新维度下向量t Xi与TxJ的点击结果？

这是我们求解新维度下决策超平面的必经之路。

这里有两种方法，

方法一：定义相应的维度转换函数，对数据完成维度转换后，再求新维度向量的点击。

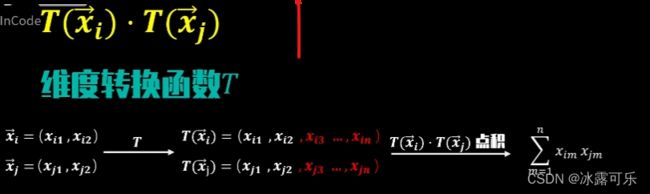
方法二：直接套用核函数kernel function，K Xi sj。
因为k Xi xj等于txi和TSJ的点击结果，
所以我们就可以通过圆维度下的向量点击结果，
直接计算出新维度的向量点击结果。

我们可以用个简单的例子比较一下方法一和二

第一种方法中，我们定义了下面的维度。

转换函数转换后，高维度向量点击结果如上，

为了实现同样的点击结果，我们可以直接套用下面的多项式和函数，
这样是不是方便了很多？

这里的第二种方法就是和技巧，用到的和函数为多项式和函数，
它的一般表达式如下，

不同参数CD的组合能够控制转换后的维度数和空间相似度，进而影响最终的角色超平面积，
因此选择合适的参数组合也十分重要。

关于如何选择参数这一块内容，一会说

多项式和函数中的常数项参数C
有着非常重要的作用，

正因为它的存在，最终点击结果的表达式中才包含了低次项到高次项的数据组合
体现出维度的多样性，假如缺少常数项参数的话，表达式中只会包括高次项。

对于这类无常数项参数C的多项式和函数来说，我们也可以将多个不同次的多项式和函数相加组合，
使其结果同时具有包底之项，以此丰富维度的多样性。

了解了这一点，对我们后续理解高斯和函数会有很大的帮助。

上面介绍的多项式和函数在参数C和D确定时也就确定了转换后的维度数了。

接下来让我们的胃口变得更大一些，对新维度数不设上限，
并要求包含从低次到无限高次全部的数据交互可能性，
组合在这个无限维度空间中求解决策超平面，

那么有没有相应的办法？

很显然，通过之前使用维度转换函数的方法，
一是不可行的无限维度意味着无限的新维度数据需要先定义存储再计算，这在技术上是不可能实现的，
那么只有依靠方法二核函数，

接下来我就要介绍最重要的核函数：
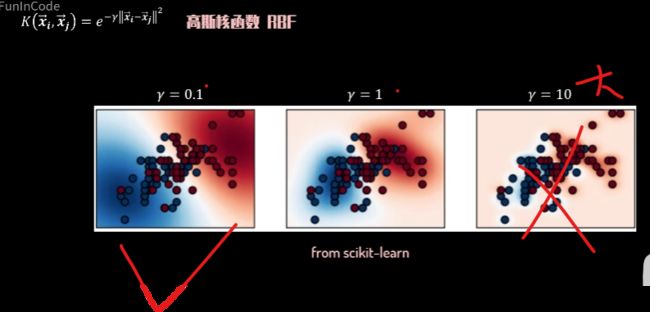
高斯核函数，也可以被称为radio basis kernel：RDF核函数，

它的表达数项，

它的值反映了两个向量的相似度大小，
由一个大于零的参数伽马值和两向量坐标点间的距离不确定。
相对的图像反映了相似度与两点距离的关系。

当伽马值确定时，两点距离越大，其相似度越向零靠近，
距离越小，相似度越向一靠近。

当我们开始变动参数伽马
距离相似度函数图像也发生变化，
伽马值越小图像越扁平，

反之，越肩窄。

扁平或肩窄，决定了高斯和函数对相似度的判断标准。

伽马值越小，图像越扁平，距离即使较远，仍然有较明显的相似度值。

而当伽马值变大，同样的距离，相似度值反而可能趋于零。

反映到算法中，它意味着在小伽马值的情况下，数据点间的相似度被放大了，
这能让数据点更容易被简单超平面划分，

而在大咖的值的情况下，除了距离非常近的数据点以外，其余数据点均与其他点缺乏相似性。
在计算分割超平面的过程中，必须要考虑到这些点各自的空间特征，
所以也较容易出现过拟合的问题。

通过观察，这些由不同伽马值组成的SVM分类效果的比较图中，

大家可以细细体会理解我刚刚说的这些内容，

那么，如何选择合适的伽马值也就非常重要了。

接下来为了计算方便，我会将伽马值设置为1/2，

我们现在对高斯和函数进行如下推导。

推导完成后，我们可以把前半部分看作常数C，
而后半部分是以自然常数e为底的指数函数。

将两向量的点击结果看做一个整体，再使用泰勒级数展开，得到下面的表达式。

而这个表达式我们就很熟悉了，它代表了无穷多个不带常数项参数C的多项式核函数
从低次到无穷高次依次排列，根据不同阶乘系数调整后再相加，

根据先前的介绍，它的结果能够体现出无限维度、数据高低、次项组合无限多样性的特点。
这样我们就实现了，在不实质性踏入无限维度的情况下，
得到了无限维度下向量相似度的结果。

正因为这一点，高斯和函数也是我最喜欢的和函数。

一般来说，面对SVI非线性分类问题时，我们可以直接使用高斯和函数。

目的就是通过核函数求解q的lambdai，再去求w和b，搞定超平面

---

SVM软间隔

今天我们进入SVM知识向量积理论部分的最后一个环节，软间隔soft margin。

在之前我们介绍了如何在不通过数学推导的情况下，
直觉理解软硬间隔的概念。

今天我们将深入理解软间隔的数学本质。
当然，如果你已经顺着我之前的节奏理解了前面关于硬间隔的数学推导，
那么今年理解软间隔就会很简单了。

看下面的例子，在这个二维空间中，

我们已经有了硬间隔，将两类数据进行了区分，
所有绿点都位于正超平面或其上方，
所有黄点都位于负超平面或其下方，
绿点的Y值为一，黄点的Y值为负一，所有点都满足约束条件。

假如我们有一个新的数据点a，很显然它不符合约束条件，
如果需要迎合这个新数据点**，硬间隔会变成这个样，间隔距离明显减少**，
那么我们就需要做出下面的选择，

选择一，采用新硬间隔，但由于间隔变窄，未来用于数据分类预测的效果将大打折扣。

选择二，继续采用原间隔，但由于新数据的加入，原硬间隔约束条件被其破坏，产生了系统损失。

这个包含损失的间隔也就是我们今天的主角。

软间隔当前我们有一个点a，违背约束条件，
不等式左边部分小于一，这个小于一违反约束的部分，
我们可以用yikexionga来量化，

你可以将其理解为当前点的损失值。

我们移动当前点的位置，观察对应损失值变化的规律。

当其不断靠近负超平面时，
我们将减号右边的部分看成一个整体，大A

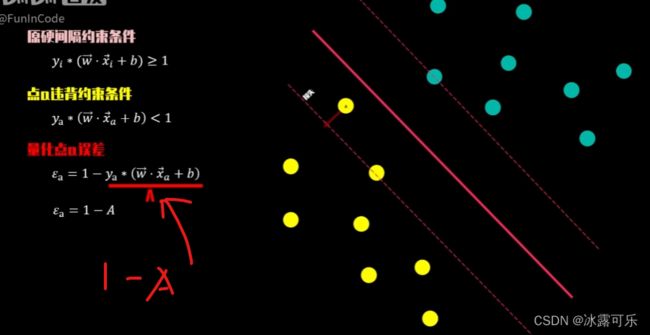
在X轴展示出来，它的值逐渐向低靠近。
yikexionga的结果体现在Y轴，其值逐渐趋于零，

移动到负超平面时，大A等于一，yikexionga为零，

之后我们顺相同方向继续移动数据点，

原约束条件A大于等于一并不会被破坏，损失值yikexionga将继续保持为零。

很显然，那些本身就符合原硬间隔约束条件的数据点的损失值始终为零。

同样的，当数据点从原先位置不断远离负超平面时，

对应的大A值也将沿着X轴向左移动，当其移动到决策超平面时，

大A等于零，此时损失值yikexionga为1，

继续移动，yikexionga也将线性增加

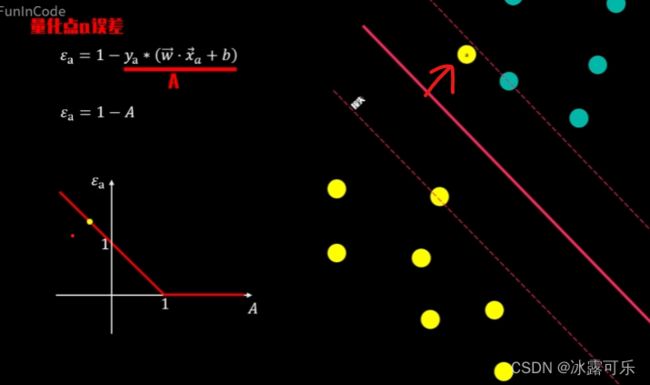
所以对任意点A，它的损失值可以用下面的损失函数来表示。

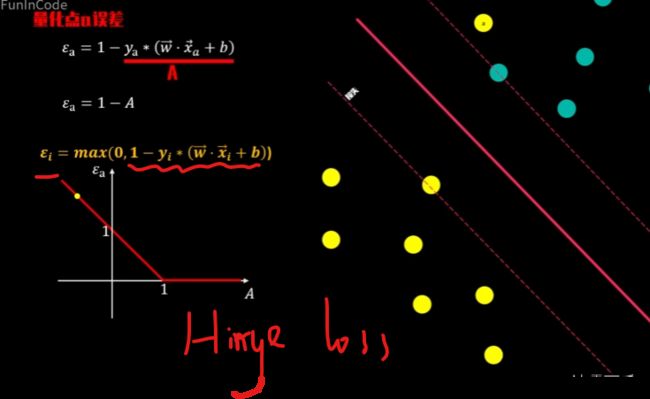
由于该函数的图形特点，我们将其称之为角列损失函数hinge loss function。
【因为它就是一个角】

在了解了软间隔的基本概念和损失函数后，
我们就可以进一步了解软间隔背后的数学优化问题了。

还记得求解硬间隔的优化问题吗？

寻找最优角色超平面等价于求解在满足约束条件的情况下
向量W程度的最小化问题。

与上面硬间隔的优化问题不同。

在求解软间隔的优化问题过程中，我们要引入损失值的概念。

首先看目标函数，我们需要同时考虑向量W程度和损失值，yikexiongi，
两者都是越小越好，

但因为W和yikexiongi会互相制约，
W长度越大，间隔越小，原始数据越不容易出现分类错误。
因此，yikexiongi的和越小，

同样的W长度越小，yikexiongi的和会越大。

所以最后的最优解中W和yikexiongi需要达到平衡，
实现两者相加的最小化，达到总体最优。

以上角列损失函数等价于下面的约束条件，

然后大家就可以使用上面硬间隔的求解方法，类似的方法去求解软间隔的优化问题了。

不过在实际操作中，我们会对目标函数的损失值部分成一个非负的参数C，
因为我们的目标是求函数的最小值解

C可以让我们控制对损失值si的容忍度。

起到惩罚FI的作用，
一个大C意味着函数值对yikexiongi大小敏感，
小yikexiongi也能够对函数值产生较大影响。

一个极大的C可以让我们无法容忍误差yikexiongi，因此，最优解中yikexiongi的值取于零。

优化问题也等价于硬间隔问题，

当C很小时函数值对误差不敏感，最优解中可以容忍较大的误差yikexiongi

因此选择合适的C。对SVM模型的最终分类效果也十分关键，

到此，所有关于SVM的知识，推导，原问题，kkt条件，对偶问题，核函数、hinge loss损失函数，硬间隔，软间隔就都讲完了

希望你在面试过程中也能游刃有余搞定这个大致的推导过程，和里面有些比价骚的操作

至少你要明白啥事hinge loss
说白了就是为了软化要求的，否则硬间隔要求太狠了。

---

总结

提示：重要经验：

1）SVM的知识，推导，原问题，kkt条件，对偶问题，核函数、hinge loss损失函数，硬间隔，软间隔
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。