从全连接网络一步步推导卷积神经网络

微信公众号：小白图像与视觉

关于技术、关注yysilence00。有问题或建议，请公众号留言。

---

主题：从全连接网络一步步推导卷积神经网络

摘要：在图像分析中，卷积神经网络（简称CNN或ConvNet）比完全连接（FC）网络具有更高的时间和内存效率。但为什么？与ConvNets相比，FC网络在图像分析方面有哪些优势？ConvNet如何从FC网络派生？CNN中的卷积一词来自哪里？这些问题将在本文中得到解答。

1.简介

图像分析面临许多挑战，例如分类，对象检测，识别，描述等。例如，如果要创建图像分类器，则即使有变化（例如遮挡，照明变化，视角等。具有特征工程主要步骤的传统图像分类管道不适合在丰富的环境中工作。即使是本领域的专家，也无法给出在不同变化下能够达到高精度的单个或一组功能。受此问题的启发，特征学习的想法应运而生。会自动学习适合使用图像的功能。这就是为什么人工神经网络（ANN）是图像分析的可靠方法之一的原因。基于诸如梯度下降（GD）的学习算法，ANN自动学习图像特征。原始图像将应用于ANN，而ANN负责生成描述它的特征。

2.使用FC网络进行图像分析

让我们看看ANN如何处理图像，以及CNN为什么有效地满足其时间和内存要求，为图1中的以下3x3灰度图像生成WRT。为简单起见，给出的示例使用较小的图像尺寸和较少的神经元数量。

图1

ANN输入层的输入是图像像素。每个像素代表一个输入。由于ANN使用1D向量而不是2D矩阵，因此最好将上述2D图像转换为1D向量，如图2所示。

图2

每个像素都映射到向量中的一个元素。向量中的每个元素代表ANN中的一个神经元。因为图像具有 3x3 = 9 像素，所以输入层中将有9个神经元。将向量表示为行或列并不重要，但ANN通常水平延伸，并且其每一层都表示为一列向量。

在准备好ANN的输入后，接下来是添加隐藏层，以学习如何将图像像素转换为代表性特征。假设存在一个包含16个神经元的单个隐藏层，如图3所示。

图3

由于网络已完全连接，这意味着第i层中的每个神经元 都连接到第i-1层中的所有神经元 。结果，隐藏层中的每个神经元都连接到输入层中的所有9个像素。换句话说，每个输入像素都连接到隐藏层中的16个神经元，其中每个连接都具有对应的唯一参数。通过将每个像素连接到隐藏层中的所有神经元， 对于这种微小的网络，将有 9x16 = 144个参数或权重，如图4所示。

图4

3.大量参数

该FC网络中的参数数量似乎可以接受。但是，随着图像像素和隐藏层数量的增加，该数量会大大增加。

例如，如果该网络具有两个隐藏层，其中神经元的数目为90和50，则输入层和第一个隐藏层之间的参数数为 9x90 = 810。两个隐藏层之间的参数数量为 90x50 = 4,500。该网络中的参数总数为 810 + 4,500 = 5,310。对于这样的网络来说，这是一个很大的数目。大小为32x32（1,024像素）的非常小的图像的另一种情况。如果网络使用500个神经元的单个隐藏层进行操作，则总计 1,024 * 500 = 512,000 参数（重量）。对于只有单个隐藏层处理小图像的网络而言，这是一个巨大的数目。必须有解决方案以减少此类参数的数量。这是CNN发挥关键作用的地方。它创建了一个非常大的网络，但参数数量少于FC网络。

4.神经元分组

即使对于小型网络，也使参数数量变得非常大的问题是FC网络在连续层的每两个神经元之间添加一个参数。如图5所示，可以给一个神经元块或一组神经元分配单个参数，而不是在每两个神经元之间分配单个参数。图3中索引为0的像素连接到索引为（0，1的前4个神经元。 ，2和3）具有4种不同的权重。如果神经元如图5所示分为4组，则同一组内的所有神经元将被分配一个参数。

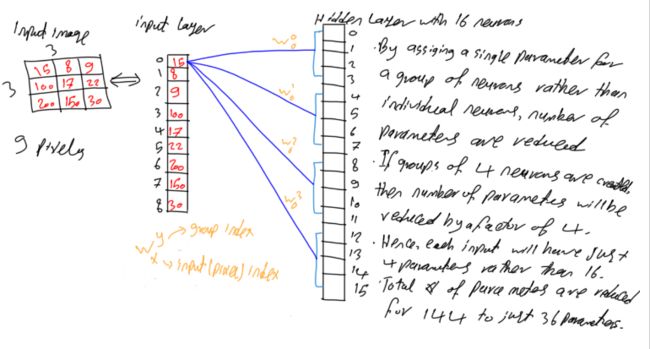图5

结果，图5中索引为0的像素将以与图6相同的权重连接到前4个神经元。将相同的参数分配给每4个连续的神经元。结果，参数数量减少了4倍。每个输入神经元将具有 16/4 = 4个 参数。整个网络将具有 144/4 = 36个 参数。它减少了75％的参数。很好，但是仍然可以减少更多参数。

图6

图7显示了从每个像素到每个组的第一个神经元的唯一连接。那就是所有丢失的连接只是现有连接的重复。假设，如图4所示，从每个像素到每个组中的每个神经元都有连接，因为网络仍然完全连接。

图7

为了简化起见，所有连接都被省略，除了所有像素之间仅连接到第一组中的第一个神经元之间的连接（如图8所示）。似乎每个组仍然连接到所有9个像素，因此它将具有9个参数。可以减少此类神经元连接到的像素数量。

图8

5.像素空间相关

当前配置使每个神经元接受所有像素。如果有一个函数f（x1，x2，x3，x4）接受4个输入，则意味着将基于所有这4个输入进行决策。如果仅具有2个输入的函数给出的结果与使用所有4个输入的结果相同，则我们不必使用所有这4个输入。提供所需结果的2个输入就足够了。这与上述情况相似。每个神经元接受所有9个像素作为输入。如果使用较少的像素将返回相同或更好的结果，则应进行检查。

通常，在图像分析中，每个像素与周围的像素（即邻居）高度相关。两个像素之间的距离越大，它们之间越不相关。例如，在图9所示的摄影师图像中，面部内部的像素与周围的周围面部像素相关。但它与天空或地面等较远像素的相关性较低。

图9

基于这样的假设，以上示例中的每个神经元将只接受在空间上彼此相关的像素，因为对所有像素进行工作都是合理的。除了可以将所有9个像素应用于每个神经元作为输入之外，还可以仅选择4个与空间相关的像素，如图10所示。将应用位于图像中（0,0）的列向量中索引为0的第一个像素。作为第一个神经元的输入，它具有3个与空间最相关的像素。基于输入图像，与该像素在空间上最相关的3个像素是索引为（0,1），（1,0）和（1,1）的像素。结果，神经元将仅接受4个像素而不是9个像素。由于同一组中的所有神经元都共享相同的参数，因此每组中的4个神经元将仅具有4个参数而不是9个参数。因此，参数总数为4x4 = 16。与图4中的完全连接网络相比，参数减少了144-16 = 128（即减少了88.89％）。

图10

6. CNN中的卷积

至此，回答了为什么CNN比FC网络更节省时间和内存的问题。使用较少的参数可以增加具有大量层和神经元的深层CNN，这在FC网络中是不可能的。接下来是获得CNN中卷积的想法。

现在，只有4个权重分配给同一块中的所有神经元。这4个权重将如何覆盖所有9个像素？让我们看看它是如何工作的。

图11显示了图10中的先前网络，但是在将权重标签添加到连接之后。在神经元内部，将4个输入像素的每一个乘以其相应的权重。该方程式如图11所示。四个像素和权重将更好地可视化为如图11所示的矩阵。先前的结果将通过将权重矩阵乘以当前4个像素一个元素的集合来实现。实际上，卷积掩码的大小应为奇数，例如3x3。为了更好地处理，本示例中使用2x2蒙版。

图11

移至索引1的下一个神经元，它将与另一组空间相关的像素一起工作，这些像素具有与索引0的神经元相同的权重。而且，索引2和3的神经元将与其他两组空间相关的像素一起工作像素。如图12所示。似乎该组中的第一个神经元从左上角的像素开始，并选择围绕它的许多像素。该组中的最后一个神经元作用于右下角像素及其周围的像素。调整中间神经元以选择中间像素。这种行为与卷积相同。该组权重集与图像之间的卷积。这就是为什么CNN具有卷积一词的原因。

图12

对于其余的神经元组，执行相同的步骤。每组的第一个神经元从左上角及其周围的像素开始。每组的最后一个神经元与右下角及其周围的像素一起工作。中间神经元作用于中间像素。

7.参考

Aghdam, Hamed Habibi, and Elnaz Jahani Heravi. Guide to Convolutional Neural Networks: A Practical Application to Traffic-Sign Detection and Classification. Springer, 2017.

更多请参考：