余弦距离及高维数据相似度计算介绍

1. 距离准则

在聊接下去的内容之前，我们首先要了解一个概念，叫距离准则：

距离准则有欧氏距离，Jaccard相似度，余弦相似度，Pearson相似度 这几种，我们来分别解释下。

欧式距离 就是指在 $m$ 维空间中两个点之间的真实距离，或者向量的自然长度（即该点到原点的距离）。在二维和三维空间中的欧氏距离就是两点之间的实际距离，所以它实现的是绝对距离。

余弦相似度 是通过计算两个向量的夹角余弦值来评估他们的相似度。

Jaccard相似度 是用于比较有限样本集之间的相似性与差异性，其中 Jaccard 系数值越大，样本相似度越高。

Pearson相似度是余弦相似度的升级版，它把每个向量都中心化了，即每个向量会减去所有向量的平均数，来实现数据更好的平衡，所以它实现的是相对距离。
————————————————

2. 余弦相似度和余弦距离

概述： 在机器学习领域中，通常将特征表示为向量的形式，所以在分析两个特征向量之间的相似性时，常用余弦相似度表示。

例如将两篇文章向量化，余弦距离可以避免因为文章的长度不同而导致距离偏大，余弦距离只考虑两篇文章生成的向量的夹角。

余弦相似度的取值范围是[-1,1]，相同两个向量的之间的相似度为1。

余弦距离的取值范围是[0,2]。

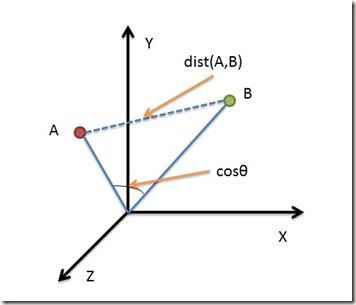
余弦相似度的定义公式为$cos(A,B)=\frac{A\cdot B}{{\Vert A\Vert }_2{\Vert B\Vert }_2}$

归一化后：${\Vert A\Vert }_2=1,{\Vert B\Vert }_2=1,{\Vert A\Vert }_2{\Vert B\Vert }_2=1$

余弦距离：$dist(A,B)=1-cos(A,B)=\frac{{\Vert A\Vert }_2{\Vert B\Vert }_2-A\cdot B}{{\Vert A\Vert }_2{\Vert B\Vert }_2}$，距离恒大于0

欧式距离：

由公式可以看出归一化后，欧式距离与余弦距离存在单调性关系。此时两种距离的值域都为[0,2]。
差分余弦距离求相似度，比直接余弦距离效果好

欧式距离与余弦距离的对比：

• 1.欧式距离的数值受到维度的影响，余弦相似度在高维的情况下也依然保持低维完全相同时相似度为1等性质。

• 2.欧式距离体现的是距离上的绝对差异，余弦距离体现的是方向上的相对差异。

3. 与欧式距离的区别

余弦距离使用两个向量夹角的余弦值作为衡量两个个体间差异的大小。相比欧氏距离，余弦距离更加注重两个向量在方向上的差异。

借助三维坐标系来看下欧氏距离和余弦距离的区别：

参考资料

[1] Python计算余弦相似性（cosine similarity）方法汇总 2022.5
[2] 相似度算法之余弦相似度 2016.7
[3] 余弦相似度 高维数据_海量高维数据与近似最近邻 2020.11
[4] 作者：CSDN博主「深度学习视觉」;