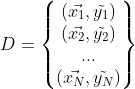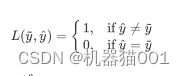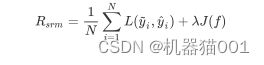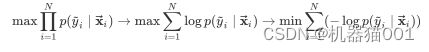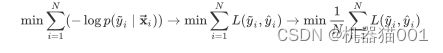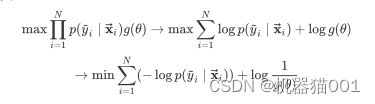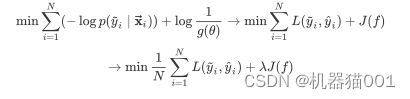机器学习基本知识（1）
目录
1、总述
2、基本概念
2.1 特征空间
2.2 样本表达
3、机器学习三要素
3.1 模型
3.2 策略
3.3 算法
1、总述
1）.机器学习的对象是：具有一定的统计规律的数据。
2）.机器学习根据任务类型，可以划分为：
监督学习任务：从已标记的训练数据来训练模型。 主要分为：分类任务、回归任务、序列标注任务。
无监督学习任务：从未标记的训练数据来训练模型。主要分为：聚类任务、降维任务。
半监督学习任务：用大量的未标记训练数据和少量的已标记数据来训练模型。
强化学习任务：从系统与环境的大量交互知识中训练模型。
3）机器学习根据算法类型，可以划分为：
传统统计学习：基于数学模型的机器学习方法。包括 SVM 、逻辑回归、决策树等。
这一类算法基于严格的数学推理，具有可解释性强、运行速度快、可应用于小规模数据集的特点。
深度学习：基于神经网络的机器学习方法。包括前馈神经网络、卷积神经网络、递归神经网络等。
这一类算法基于神经网络，可解释性较差，强烈依赖于数据集规模。但是这类算法在语音、视觉、自然语言等领域非常成功。
4）没有免费的午餐 定理( No Free Lunch Theorem:NFL )：对于一个学习算法 A ，如果在某些问题上它比算法 B好，那么必然存在另一些问题，在那些问题中 B 比 A 更好。因此不存在这样的算法：它在所有的问题上都取得最佳的性能。因此要谈论算法的优劣必须基于具体的学习问题。
2、基本概念
2.1 特征空间
1）输入空间 ：所有输入的可能取值；输出空间 ：所有输出的可能取值。 特征向量表示每个具体的输入， 所有特征向量构成特征空间。
2） 特征空间的每一个维度对应一种特征。
3）可以将输入空间等同于特征空间，但是也可以不同。绝大多数情况下，输入空间等于特征空间。模型是定义在特征空间上的。
2.2 样本表达
1) 通常输入实例用
表示，真实标记用
表示，模型的预测值用
表示。
具体的输入取值记作
；具体的标记取值记作
；具体的模型预测取值记作 
。
2. 所有的向量均为列向量，其中输入实例的特征向量记作 :（假设特征空间为n维）
3) 训练数据由输入、标记对组成。通常训练集表示为：
输入、标记对又称作样本点。假设每对输入、标记对是独立同分布产生的。
4) 输入和标记可以是连续的，也可以是离散的。 为连续的：这一类问题称为回归问题。为离散的，且是有限的：这一类问题称之为分类问题。
输入和标记 均为序列：这一类问题称为序列标注问题。
3、机器学习三要素
机器学习三要素：模型、策略、算法。
3.1 模型
1）模型定义了解空间。监督学习中，模型就是要学习的条件概率分布或者决策函数。模型的解空间包含了所有可能的条件概率分布或者决策函数，因此解空间中的模型有无穷多个。
模型为一个条件概率分布,解空间为条件概率的集合：
。其中：
为随机变量， 
为输入空间，
为输出空间。
通常F是由一个参数向量 ![\vec{\theta }=[\theta _{1},\theta _{2},...,\theta _{r}]](http://img.e-com-net.com/image/info8/03147677c14340c195af638977fc3f27.gif){kind=small}
决定的概率分布族：
。其中： 
只与 有关
，称 为参数空间。
模型为一个决策函数：
解空间为决策函数的集合
： 。其中： 为变量， 为输入空间，为输出空间。
通常 F是由一个参数向量 决定的函数族：
。其中： 
只与 有关，称 为参数空间。
2）解的表示一旦确定，解空间以及解空间的规模大小就确定了。
如：一旦确定解的表示为：
，则解空间就是特征的所有可能的线性组合，其规模大小就是所有可能的线性组合的数量。
3）将学习过程看作一个在解空间中进行搜索的过程，搜索目标就是找到与训练集匹配的解。
3.2 策略
策略考虑的是按照什么样的准则学习，从而定义优化目标。
1）损失函数: 对于给定的输入 ，由模型预测的输出值与真实的标记值可能不一致。此时，用损失函数度量错误的程度，记作 
，也称作代价函数。
常用损失函数：
①0-1损失函数：
②平方损失函数：
③绝对损失函数：
④对数损失函数：
=
其物理意义是：二分类问题的真实分布与模型分布之间的交叉熵。
训练时采用的损失函数不一定是评估时的损失函数。但通常二者是一致的。因为目标是需要预测未知数据的性能足够好，而不是对已知的训练数据拟合最好。
2）风险函数
通常损失函数值越小，模型就越好。但是由于模型的输入、标记都是随机变量，遵从联合分布 ， 因此定义风险函数为损失函数的期望。学习的目标是选择风险函数最小的模型。
3）经验风险
经验风险也叫经验损失， 经验风险是模型在训练集D上的平均损失:
（基于损失函数求取）。
经验风险最小化 ( empirical risk minimization:ERM ) 策略认为：经验风险最小的模型就是最优的模型。经验风险是模型在训练集D上的平均损失。结构风险是在经验风险上叠加表示模型复杂度的正则化项（或者称之为罚项），它是为了防止过拟合而提出的，结构风险最小化 ( structurel risk minimization:SRM ) 策略认为，结构风险最小的模型是最优的模型。
模型关于D的结构风险定义为：
其中： 
标准模型复杂度，f越复杂，则越大。
4）极大似然估计
极大似然估计就是经验风险最小化的例子，已知训练集 D，根据 出现概率最大，有：
定义损失函数为=(对数损失函数)，则有：
即：极大似然估计 = 经验风险最小。
5）最大后验估计
最大后验估计就是结构风险最小化的例子，已知训练集D，根据D出现概率最大：
定义损失函数为=(对数损失函数)，则有：
即：最大后验估计 = 结构风险最小化
3.3 算法
算法指学习模型的具体计算方法。通常采用数值计算的方法求解，如：梯度下降法