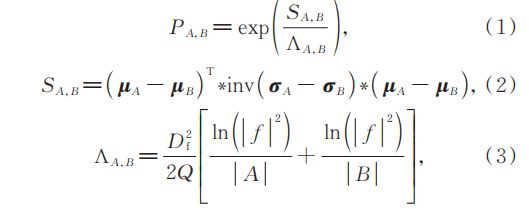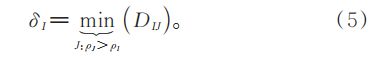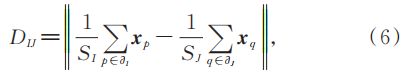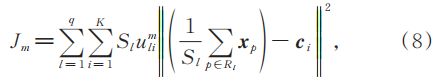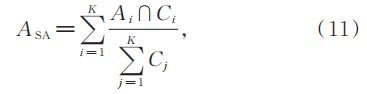论文研究 | 快速自动模糊 C-均值聚类彩色图像分割算法

前面分享了机器视觉缺陷检测应用方面的论文，今天想分享关于图像分割领域的研究。图像分割是计算机视觉和图像理解中最重要的研究课题之一，该论文提出了一种快速自动的 FCM 彩色图像分割算法，所提算法的计算复杂度较低、运行时间较少、分割精度较高。

1 引 言

略。

 2 所提算法

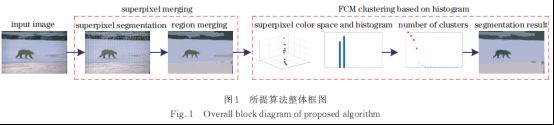
传统 FCM 算法计算复杂度高且无法自动确定聚类数目，本实验组提出了一种快速自动的 FCM 彩色图像分割算法。首先通过改进的 SLIC 超像素算法预分割图像，将基于单个像素的 FCM 算法转化为基于超像素区域的 FCM 算法，降低算法的计算复杂度；其次利用密度峰值算法自动确定聚类数目，提高算法的灵活性；最后利用直方图聚类完成彩色图像分割。所提算法整体框如图 1 所示。

 2. 1 改进的超像素算法

传统 SLIC 超像素算法［14］是通过多个种子点实现的，而有些种子点可能来自同一区域，因此同一区域可能被分割成多个超像素区域，产生过分割现象。本研究提出了一种新的区域合并策略，在超像素分割之后引入该策略，消除过分割现象。首先利用原始 SLIC超像素算法预分割图像，产生超像素区域。其次，计算每个超像素区域及其相邻区域的像素平均值和方差。然后，将低于最小像素数的区域与其相邻区域合并（这里将最小像素个数设置为 10，低于该最小像素个数的区域认为是面积很小的超像素区域，该区域对后续分割结果的影响很小，因此将其与相邻像素合并），并更新合并后的区域的像素平均值和方差。两个区域的合并概率 P A，B 的表达式为

式中：SA，B 为区域 A 和区域 B 的相似性度量；Λ A，B 为区域合并惩罚函数；μ A 和 μB 为区域 A 和 B 的像素平均值；σ A 和 σ B 为区域 A 和 B 的方差；Df 为图像 f 的动态范围（如 8 bit 图像的动态范围为 256）；Q 为正则项；| ⋅ |为所包含的元素数量；inv 为矩阵求逆运算；*为矩阵之间的乘法运算。由式（1）可知，P A，B 最小的相邻区域对应于高度相似的区域，应首先合并这些区域。最后，反复迭代上述过程，直到 P A，B ≤ η（η 为合并阈值）完成超像素分割过程。合并阈值 η 是人为设定的，大量实验结果表明，η = 3.5 时可得到较好的分割结果。图 2 为采用 5 种超像素算法对 3 幅彩色图像进行分割的结果。从图中可以看出，线性光谱聚类（LSC）［15］、均值漂移（Mean shift）［16］、分水岭变换（WT）［17］和 MMGRWT［10］的结果中都存在过分割现象，而所提改进的超像素算法能明显抑制过分割。［图 3（b）、（c）］为所提算法分割过程中的颜色空间变化情况，［图 3（b）］为原始图像的颜色空间，［图 3（c）］为改进的超像素算法分割后的颜色空间。从图中可以看出，预分割之后的超像素区域个数远小于原始像素个数，大大简化后续分割过程。由此可知，通过超像素预分割将传统基于单个像素的FCM 算法转化为基于超像素区域的 FCM 聚类，计算复杂度由 H × W × K × T 降为 N × K × T，其中 H 和 W分别为图像的宽和高，K 为聚类数目，T 为迭代次数，N为超像素区域个数，达到了降低复杂度的目的。

 2.2 DP 算法自动确定聚类数目

DP 算法可以根据决策图选择聚类个数，实现自动聚类，但该算法产生的相似度矩阵庞大，导致内存溢出、计算成本较高。通过改进的超像素算法，原始图像中具有相同特征的像素被划分到同一超像素区域，因此将原始基于逐像素的 DP 算法转化为基于超像素区域的 DP 算法，可有效降低算法的计算成本。基于超像素区域的 DP 算法假设一个聚类中心的密度通常高于其周围的点，并且一个聚类中心与其他密度较高的聚类中心之间的距离往往较大。根据上述超像素算法和 DP 算法，局部密度 ρI 的表达式为

式中：I ≥ 1；J ≤ N；DIJ 为超像素区域 ∂I 和 ∂J 的欧氏距离；SJ 为在第 J 个超像素区域的像素个数；dc 为截止距离 。 δI 为 区 域 ∂I 与 其 他 密 度 较 高 区 域 之 间 的 最小距离：

 对于密度最高的超像素区域 δI = maxJ ( DIJ )。为了加速计算，DIJ 的表达式为

 式中：xp 和 xq 为 p 和 q 点的像素值。最后，决策图为局部密度与最小距离的乘积：

由决策图中各点之间的距离自动确定聚类数目，实现聚类数目的自动确定。［图 3（f）］为使用 DP 算法生成的决策图，该图可以自动确定聚类数目。

2. 3 目标函数

为降低 FCM 算法的计算复杂度，实现聚类数目的自动确定，所提快速自动的模糊 C-均值聚类彩色图像分割算法的目标函数为

式中：l为颜色等级，1 ≤ l ≤ q，q 为像素的亮度等级数； K 为聚类个数；Sl 为第 l 个超像素区域 Rl 的像素个数； uli 为第 l 个超像素区域属于第 i 个聚类簇的隶属度；m为模糊度因子，一般设置为 2；xp 为超像素区域的像素值；ci 为第 i 个聚类簇的聚类中心。因为 l ≪ N，所以所提算法的计算复杂度明显降低。ci 和 uli 可通过拉格朗日乘子法得到：

通过式（9）和式（10）更新 ci 和 uli，输出隶属度矩阵，并将每个像素分配给隶属度最大的聚类簇中，完成图像分割。所提算法具体步骤如下：

1）设置参数，包括超像素个数 K，模糊隶属度因子 m，迭代误差 ε和最大迭代次数 T；

2）利用式（1）~（3）计算超像素图像，获得图像的超像素区域；

3）利 用 式（4）~（6）生 成 决 策 图 ，并 确 定 聚 类数目；

4）初始化隶属度矩阵 uli；

5）利用式（9）计算聚类中心 ci；

6）利用式（10）计算隶属度矩阵 u；

7）利用式（8）计算目标函数 Jm；

8）判断| J am - J a - 1 m |≤ ε 是否成立，若是则执行步骤 9），若否则返回步骤 4）；

9）返回隶属度，并将所有像素分配到隶属度最大的聚类簇中，完成分割。

3 实验结果与分析

为了验证算法的性能，选用 BSDS500［18］、AID［19］ 和 MSRC［20］数据库的彩色图像为测试图像，并将结果与 FCM［5］、SFFCM［10］、FCM_SICM［11］和 AFCF［12］进行比较，性能指标选用分割精准度（SA）、模糊分割系数（VPC）、模糊分割熵（VPE）、视觉效果和运行时间。

式中：Ai 为分割结果中第 i 个聚类簇的像素集合；Ci 为参考图像中第 i 个聚类簇的像素集合。SA 越大，分割性能越好。模糊分割系数和模糊分割熵的表达式为

 VPC越大分割效果越好，VPE越小分割效果越好。

3. 1 彩色图像分割结果

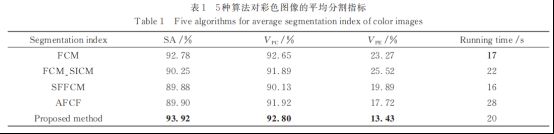
对不同彩色图像的实验结果如图 4 和图 5 所示，对BSDS500 中的彩色图像的平均分割性能指标如表 1所示。

在对#124084 图像进行分割时，分割性能最差的是 FCM 算法和 FCM_SICM 算法，FCM 算法将背景像素 误 分 割 为 目 标 像 素 ，产 生 虚 假 分 割 现 象 ，而FCM_SICM 算法则将目标像素过度模糊，使得分割结果边缘模糊和目标虚化。#145086 图像中，SFFCM 算法将背景的天空和白云误分割为一类，导致视觉效果较 差 。 同 样 ，在 对 #28083 图 像 进 行 分 割 时 ，FCM_SICM 将绿地和山丘误分割为一类，产生虚假分割。特别注意的是，FCM_SICM 分割#48017 时，分割结果为全黑图像，原因为 FCM_SICM 算法主要是针对噪声图像而设计的算法，该算法最主要的一点即为在聚类过程中适当模糊图像，从而抑制噪声对聚类结果的影响，而当图像被噪声污染较轻或没被噪声污染时分割 性 能 显 著 降 低 。 所 提 算 法 利 用 超 像 素 算 法 降 低FCM 的计算复杂度，并用 DP 算法生成决策图，自动确定聚类数目。超像素算法能平滑纹理细节并保留目标的结构信息，因此所提算法分割性能更好。

表 1 为 5 种算法对 BSDS500 数据库的测试图像分割时的平均性能指标。由表 1 可知：所提算法在 SA、VPC 和 VPE 方面均优于其他几种算法，表明所提算法的性能更优；而在运行时间方面，运行时间较少的是原始 FCM 算法。主要原因为其他 FCM 变体算法都在原始 FCM 基础之上引入其他加强运算，因此运行时间较长，值得注意的是，SFFCM 算法的运行时间要少于原始 FCM，引起该结果的主要原因为 SFFCM 算法不仅利用超像素算法降低算法的复杂度，同时将基于像素的聚类转化为基于直方图的聚类，因此运行时间比原始 FCM 算法要少。利用所提算法对 AID 数据库的遥感图像和 MSRC 数据库的彩色图像的分割结果如图 5 所示。从图中可以看出，所提算法对不同类型的彩色图像均有较好的分割结果，因此在应用层面，所提算法可较好分割目标简单的遥感图像和对比度鲜明的彩色图像，相比于近几年应用广泛的深度学习算法，所提算法更加简单高效，且对硬件的要求较低。

3. 2 计算复杂度分析

 

计算复杂度是评价算法性能的重要指标，然而由于编程思想的不同，精确的计算复杂度很难获取，因此本研究通过比较聚类算法目标函数的时间复杂度来评价各类算法的性能。5 种算法的时间复杂度如表 2 所示，其中 H 和 W 为原始图像的宽和高、N 为超像素区域个数、K 为聚类数目、T 为迭代次数、T M 和 T W 为 MMGRWT 的计算步骤。从表 5 可以看出，计算复杂度最高的SFFCM，其复杂度为 O ( n5 )，而所提 算 法 由 于 引 入 了 超 像 素 简 化 算 法 ，复 杂 度 仅 为O ( n3 )。

4 结 论

提出了一种快速自动的 FCM 彩色图像分割算法。针对原始 FCM 算法计算复杂度高的问题，提出了一种基于超像素预分割的快速 FCM 算法，将传统基于单个像素的 FCM 算法转化为基于超像素区域的 FCM 算 法，降低了计算复杂度，利用改进的 DP 算法实现了聚类数目的自动确定，提高了算法灵活性，最后通过基于直方图的 FCM 聚类完成图像分割。不同类型的彩色图像分割实验结果表明，相比 FCM 算法、SFFCM 算 法、FCM_SICM 算法和 AFCF 算法，所提算法的计算复杂度较低、运行时间较少、分割精度较高。但所提算法对噪声的鲁棒性较差，如何提高算法的抗噪声性能将是下一阶段的研究目标。

5 参考文献

略。

感兴趣的同学可以去知网上下载此论文。

---

文章来源：王超 1*，王永顺 1，狄凡 2. 快速自动模糊 C-均值聚类彩色图像分割算法 [J]. 激光与光电子学进展, 2022,59(22) 

---