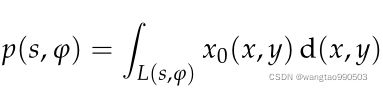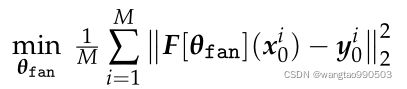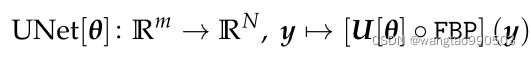2021AAPM大赛第一名技术报告Designing an Iterative Network for Fanbeam-CTwith Unknown Geometry 阅读笔记
什么是第一名的含金量呢？他的RMSE直接领先最前沿方法一个数量级！
文章中多次提到了 forward model / operator，于是我进行了一些查阅，给出个人的一些理解：
作为 forward model 实际上指的就是输入求解输出的求解（推演）过程，与之相对应的就是反演，又叫逆问题求解。在本文中指的就是将稀疏视图CT求解成正常剂量CT的过程。
数据一致性：是指要求预测结果与标签一致、或者说处于同一分布。
1. 介绍
关于深度学习在重建领域是否可以得到可靠稳定的结果一直有所争议，作者表示不服，于是他参加这个比赛去证明数据驱动的恢复工作流可以实现(接近)精确的图像恢复。
作者的方法是基于如下：
High reconstruction accuracy is only possible when the forward model is explicitly incor-
porated into the reconstruction mapping, e.g., by an iterative promotion of data-consistent
solutions.只有当正向模型被明确地结合到重建映射中时，高重建精度才是可能的，例如，通过数据一致解决方案的迭代提升。
作者贡献如下：
-
鉴于精确的正演模型未知，作者对潜在的扇束几何形状进行数据驱动的估计。这是通过以类似深度学习的方式(即，通过具有反向传播/自动微分的梯度下降)将通用的参数化扇束算子拟合到所提供的正弦图图像对来实现的。作者希望这种方法可以在几何校正和前向算子（forward operator）校正的情况下进一步使用。特别是，我们目前正在探索一种基于正弦图一致性条件的无监督识别策略。
-
我们提出了一个概念简单，但功能强大的深度学习工作流，它将后处理UNet [RFB15]变成了一个迭代重建方案。从技术角度来看，其大部分设计组件之前已在文献中报道过。然而，整个策略似乎是新颖的，并且在几个方面不同于更常见的展开网络，包括:(a)我们使用预先训练的UNet作为计算主干；(b)数据一致性受到L2梯度步骤的启发，但是利用滤波反投影而不是常规伴随投影。我们认为，所提出的策略也将用于其他逆问题，因为它在均方根误差(RMSE)方面优于其他最先进的数据驱动方法，如学习原始对偶算法一个数量级。
2. 方法
在本节中，作者将简要概述他们的方法，以及一些设计选择的动机。
Step1 Data-Driven Geometry Identification（数据驱动的几何识别）
重建流水线的第一步是从提供的训练数据中学习未知的正向算子。断层扇形束测量的连续版本基于计算线积分：
其中
是未知图像，
表示扇束坐标中的一条线，即
是扇束旋转角度，
用于编码 the 传感器位置。在理想情况下，扇束模型由下列几何参数确定（见图1）：
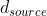- X射线源到原点的距离；
- 探测器阵列到原点的距离；
- 探测器的元件数量；
- 探测器元件沿阵列的间距；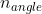
- 扇束旋转角度的数量；![\varphi \in \left [ 0, 2\pi \right ]^{n_{angle}}](http://img.e-com-net.com/image/info8/c656c6be8226455b8001bb205f0251dd.gif)
- 旋转角度的离散列表，是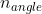个离散的0-2pi之间的值。
图1. 决定扇束CT模型几何形状的参数图示
这里假设积分只沿有限条线测量，由m := * 确定。在AAPM DL-稀疏视图挑战中，所得到的前向算子是严重不适定的，因为只获得了几个扇束旋转角度的测量值。此外，几何设置不向挑战参与者公开，只知道进行了扇形束测量。
我们已经通过数据驱动的估计策略解决了这种信息缺乏的问题，该策略将上述一组参数与给定的训练数据相匹配。为此，我们首先观察到前面的参数化是多余的（没搞懂咋就多余了，看后续的意思就是把置为1后只需要四个参数即可描述扇束现状，PS：实际上是五个，1就不算了吗！？！），并且不失一般性，我们可以假设= 1(通过适当地重新调整)。此外，如果视场角γ已知，则关系式：
公式 2-1
这一关系可以消除另外一个参数，因此，扇形束的几何形状可以由缩减的参数集（，，，
）确定。
训练数据提供成对的离散图像
及其模拟的扇形波束测量值
，由此可以导出维数 = 128和= 1024。我们将视场确定为 
= arcsin(256/)，使得离散图像中的最大内切圆恰好包含在每个扇形线内，这是扇束 CT 的常见选择。因此，（2.1）变形为：
变形过程图解：
此时，四个必要参数 （，，，）已知了俩 = 128和= 1024，剩下两个正是该步骤的难点。
为此，作者在 PyTorch 中从头开始实现了离散扇束变换（连同其相应的滤波反投影）。实现的一个独特方面是使用矢量化数值积分，它可以通过自动微分来有效计算关于几何参数的导数。此功能可用于数据驱动的参数识别，例如，通过梯度下降。更准确地说，作者对正向模型使用光线驱动的数值积分，并使用像素驱动和基于正弦图重加权的滤波反投影（使用汉明滤波器）。除了参数 (dsource,ϕ)，我们还分别为正向和逆变换引入了可学习的比例因子 
和 
。与实际的物理距离单位相比，它们解释了在选择距离离散化单位时的模糊性（这句话没太看懂，有想法的同学在评论区交流一下）。
如前所述，我们以类似深度学习的方式估计实现的前向算子 ![F\left [ \theta _{fan} \right ] \in \mathbb{R}^{m*N}](http://img.e-com-net.com/image/info8/d22aef771f5a4b2a96b18d12085195ed.gif){kind=small}
的自由参数 
（1+1+128）：计算导数
的能力允许我们通过求解具有梯度下降的变体（详见备注 2.1）公式2-2（后文好像把它当作了数据一致性层，经过阅读发现不是，我的问题）：
公式 2-2
来利用 M = 4000 个正弦图-图像对
。
最后，我们在保持已经得出的参数固定的前提下通过公式
确定
备注 2.1：
-
显然，公式 (2.2) 是非凸的，因此尚不清楚梯度下降是否能够准确估计基础扇束几何形状。事实上，标准梯度下降被发现对
的初始化非常敏感，并且陷入了糟糕的局部最小值。为了克服这个问题，我们通过坐标下降来解决（2.2），它以单独的学习率交替优化 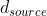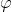，， 。发现该策略有效地解释了不同参数的梯度幅度的巨大偏差。事实上，我们观察到 的快速收敛和可靠识别，与初始化无关。 -
原则上，（2.2）的策略只需要很少的训练样本就可以成功。然而，在验证所概述策略对测量噪声的鲁棒性时，我们观察到使用更多的训练数据是有益的。
-
在估算出准确的扇束几何形状之后，我们仍然注意到前向模型中存在系统误差。我们怀疑这是由于与 AAPM 挑战的真正正向模型相比，数值积分的细微差异造成的（数值积分是在定积分难解或不可解时求取近似解的积分方法）。作为补偿，我们计算训练集上的（逐像素）平均误差，作为模型偏差的附加校正。
Step2 Pre-Training a UNet as Computational Backbone （骨干网）
我们重建方案的核心是由标准的 UNet 架构 ![U\left [ \theta \right ]:\mathbb{R}^{N}\rightarrow \mathbb{R}^{N}](http://img.e-com-net.com/image/info8/005ef1d610e24553985816388bbb1361.gif){kind=small}
形成的。它首先被用作残差网络来后处理稀疏视图过滤的反投影图像，即，我们考虑重建映射
其中m=128*1024，是一个正弦数据的大小（*）；N是图像大小（这么说UNet[]是直接由正弦域映射到图像域，而U[]才是图像到图像？上面右边的公式似乎佐证了这一说法。）；可学习参数 θ 是从挑战赛提供的 M = 4000 个正弦图-图像对 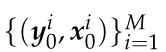的集合中训练出来的。这是通过标准的经验（为依据的）风险最小化来实现的，即通过（近似）求解：
公式 2-3
选择 µ = 10−3。这个最小化问题由 400 个epoch 的小批量随机梯度下降和 Adam 优化器处理，初始学习率为 0.0002，批量大小为 4。
备注 2.2：
步骤2的后处理（post-processing）策略率先在Low-dose CT via convolutional neural network、A deep convolutional neural network using directional wavelets for low-dose X-ray CT reconstruction两篇中使用，而后被Low-dose CT with a residual encoder-decoder convolutional neural network、Deep convolutional neural network for inverse problems in imaging等推广。由于具有跳跃连接的多尺度编码器-解码器结构，UNet 架构在处理图像到图像问题方面非常有效。因此，求解 (2.3) 通常开箱即用，不需要复杂的初始化或优化策略。使用更强大或内存效率更高的网络将是有益的，例如，请参阅下面的 Tiramisu 网络的结果。然而，我们更愿意让我们的工作流程尽可能简单，因此决定坚持使用标准 UNet 作为主要的计算构建块。
Step 3 – Constructing an Iterative Scheme.构建迭代方案
这一步中讨论主要的重建方法。它通过如下迭代过程包含了步骤1中的（近似）正向模型F（and the associated inversion by the FBP，以及由FBP进行的相关反转）：
公式 2-4
对于可学习的参数![\theta =\left [ \widetilde{\theta},\lambda _{1},\lambda _{2},\lambda _{3},\lambda _{4} \right ]](http://img.e-com-net.com/image/info8/b98c818d45d6432a976d635efb5f6b1a.gif){kind=small}
和第 k 个数据一致性层（Data Consistency）：
x投影成正弦图后减去y，再反投影成图像作为残差，然后再作为。。梯度被减？
ItNet 通过与 (2.3) 类似的经验风险最小化来训练，其中 µ = 10−4。我们运行 500 epochs小批量随机梯度下降和 Adam，初始学习率为 8·10−5，批量大小为 2（在 250 epochs后重新启动 Adam）。UNet 参数 
由步骤 2 中获得的权重来初始化。
在下文中，我们将简要讨论（2.4）中架构的核心方面，并激发一些重要的设计选择：
- ItNet 的计算核心是由 UNet 架构形成的。这与前几代展开迭代方案形成对比，后者依赖于基本卷积块。我们发现利用类似 UNet 的图像到图像网络作为中央图像增强块的功效是有利的。这与最近最先进的架构一致，这些架构也利用了各种先进的子网络。有点令人惊讶的是，在所有四次迭代（权重共享）中使用相同的 UNet 是有益的。
-
我们观察到，通过步骤 2 的后处理权重去初始化 UNet 参数
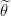至关重要。这不仅提高了收敛速度，而且还显着提高了最终精度（见图 2）。换句话说，我们的结果表明，将 UNet 块初始化为后处理单元可以找到更好的局部最小值。据我们所知，这种效果尚未在文献中报道。我们强调，这种初始化策略是通过使用足够强大的后处理子网络来实现的。 -
我们的数据一致性层受到损失
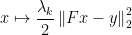的梯度步骤的启发，这将导致更新 
。我们通过用过滤的对应 FBP 替换未过滤的反投影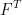 
来尝试避开这种更新。这种修改导致显着改进的结果有两个原因：（a）它抵消了未经过滤的反投影正在平滑（过滤）的事实； (b) 它产生具有正确比例的像素值的图像。因此，我们将生成的 ItNet 解释为类似工业的迭代 CT 算法（例如，参见 [WN19]），而不是神经增强凸优化方案。
在我们的实验中，通过计算（2.4）中超过四次的迭代，我们只看到了微小的影响。然而，通过以下的后期训练策略，准确性得到了提高。首先，通过多一次迭代来扩展ItNet。
其中通过公式2-4的优化权重对K=1，2，3，4，5进行初始化。然后保持前三个Unet的权重固定训练最后两次迭代（没有权重共享）来微调。获得的改进表明，在通过更多迭代增加模型容量与优化结果网络的难度之间存在权衡。这种迭代训练策略的系统研究留待未来研究。
权重 λk 的初始化和训练对 ItNet 和 ItNet-post 的准确性有相当大的影响。我们发现 λ = [λ1, λ2, λ3, λ4] 通常收敛到 {λ1 < λ2 < λ3 ? λ4} 在 ItNet 的足够多的训练 epoch 之后。为了进一步加快训练速度，我们使用通过预训练发现的初始化 λ = [1.1, 1.3, 1.4, 0.08]。
类似地，ItNet-post 在 k = 1、2、3 以及 λ4 = 1.0 和 λ5 = 0.1 时使用 ItNet 的最终值进行初始化。我们怀疑对这些标量权重的系统研究可能会导致进一步的性能提升和更常规的训练过程。特别是，将它们与 UNet 权重的训练分离可能是有益的。
微调：
为了提高我们网络的整体性能，我们还应用了以下按重要性排序的“技巧”：
- 由于统计波动，尽管使用相同的训练管道，网络通常表现出略微不同的重建误差。因此，为了计算我们的最终重建，我们集成了 10 个网络，每个网络都在训练集的不同分割上进行训练。
-
由于小批量的训练，我们将 UNet 架构的批量规范化替换为组规范化（ group normalization）。
-
我们为 UNet 架构配备了一些记忆通道，即实际上有一个
。虽然原始图像增强通道没有改变，但附加通道的输出通过 ItNet 传播，起到隐藏状态的作用（本着循环 NN 的精神）。对于我们的实验，我们选择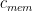 
= 5。 -
偶尔重新启动网络的训练是有益的，例如，见图 2。
以下修改并未导致性能提升，因此被省略：
-
通过使其中一些组件是可学习（例如过滤器）来改进步骤 1 中的 FBP。虽然这有利于 FBP 本身的重建质量，但它会导致 UNet 和 ItNet 的结果更差。这表明基于模型和基于数据的方法的组合最受益于精确和未更改的物理模型。
-
在 ItNet 的测量域中添加额外的卷积块。
-
通过合并 RMSE 或“L1-范数”来修改标准的“L2-损失”。
-
利用不同的优化器，例如 RAdam、AdamW、SGD 或 MADGRAD。
3. 结果
因为挑战赛的相似性比较指标就是RMSE，所以本报告也与之相同。为了比较，我们还考虑了通过更先进的 Tiramisu 架构。此外，我们还训练了迭代学习的原始对偶 (LPD) 方案（通过用 FBP 替换未过滤的反投影稍作修改）。
在图 2 中，我们首先将训练管道的 RMSE 损失曲线可视化，即 UNet ， ItNet + restart ， ItNet-post + 2 × restart。此外，表 1 中报告了所有考虑的网络的平均性能。为了给人一种视觉印象，可以在图 3 中找到来自验证集的图像重建。最后，我们分析了数据一致性方面图 4. 该图表明，如果可以使用精确的前向模型，ItNet-post 的性能仍然可以提高。这一结论也得到以下观察结果的支持：即使在第 1 步的参数识别方面的微小改进也会导致 ItNet-post 的准确度显着提高。
图2 损失曲线和网络训练。
前两个图表明，与 UNet 的后处理相比，ItNet 将 RMSE 提高了大约一个数量级。此外，我们的 UNet 初始化策略的增益可以在第二张图中看到。最后两个图分别说明了重新启动和训练后策略的优势。请注意，我们在训练集和验证集上显示 RMSE 而不是实际的 'L2-losses，它们的行为相似.
图3 重建结果。我们显示验证图像的重建。
第一行将挑战提供的 FBP 与我们自己的 FBP 进行比较（参见步骤 1）。第二行将 Tiramisu 的后处理与（集成的）ItNet-post 进行比较。地面实况图像被省略，因为它在视觉上与 ItNet-post 没有区别。
图4 数据一致性。
第一个图像通过显示来自验证集的正弦图-图像对 (y0, x0) 的误差 y0 - F(x0) 来分析我们正向模型的准确性。中间的 y0 - F · ItNet-post(y0) 的可视化在视觉上几乎无法区分，这表明 ItNet-post 继承了步骤 1 的不准确性。因此，如果更准确的前向，ItNet-post 将允许更好的结果模型可用。与 y0 - F·Tiramisu(y0) 进行比较也很有趣：右边的图像显示出相当大的误差，这表明 Tiramisu 的后处理存在数据一致性不足的问题。所有图像都显示在相同的动态范围内。
众所周知，验证集在验证中不包含真实经过，即label，所以上述误差指的是作为feature的正弦图和图像之间的差异。
文章的内容就到这里，到目前为止大多内容都是直接翻译，随后我会反复阅读并复现代码，各位感兴趣的读者可以关注阅读。
代码阅读已经完成，将感悟和难点加在了注释中，需要的小伙伴可以在我的资源中下载