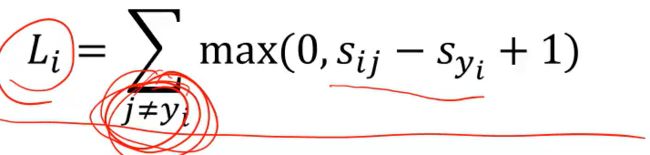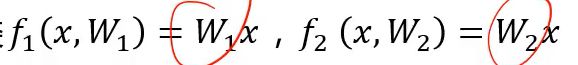计算机机器视觉原理之分类器2
计算机视觉
-
- 一.对于损失函数
- 二.正则项与超参数
- 三.优化算法
- 参数优化
- 梯度下降算法
- 梯度计算:
- 随机梯度下降算法
- 小批量梯度下降算法
- 四.数据集划分
- K折交叉验证
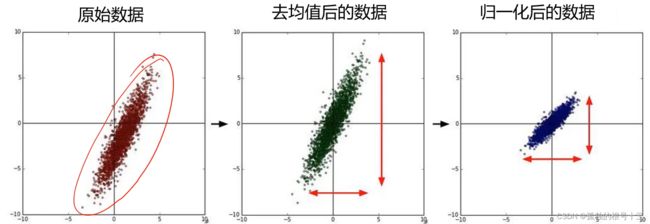
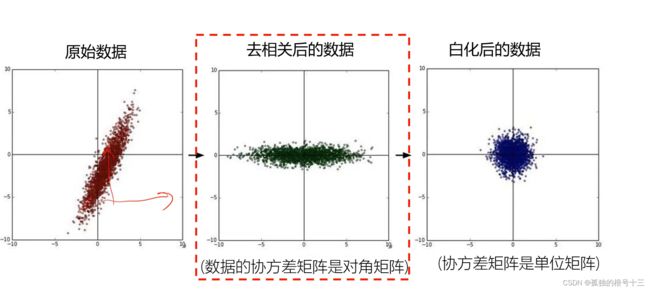
- 五.数据预处理
一.对于损失函数
损失函数:

单样本的多累支撑向量机损失:
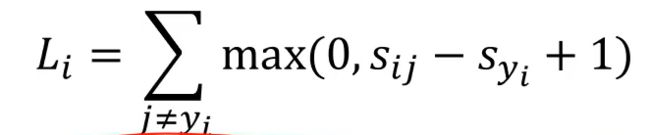
线性分类器:
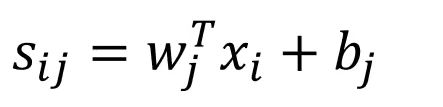
1.多类支撑向量机损失L;的最大/最小值会是多少?
最大:MAX;最小值:0
2:如果初始化时w和b很小,损失L会是多少?
令w和b为0,Sij恒等于0,带入公式,Li为类别数的个数,L为1,这种情况可以验证编码的正确性,初始化w与b为0,正确L得到1,其他就说明编码错误。
会出现自己和自己相比的情况,Li会加1,其实对损失的影响不大,只是这一项加进来意义不大,就没加
4:在总损失L计算时,如果用求和代替平均?
实际上没什么影响,只是将数放大了N倍,最大最小都放大了N倍
5:如果使用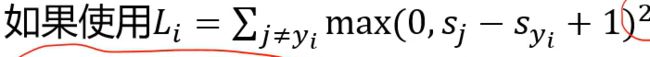
将所有的值放大一个平方,会让分类器的性能发生细微的变化
二.正则项与超参数
问题:假设存在一个W使损失函数L=0,这个W是唯一的吗?
不是唯一的
,其中,W2=2 W1。对于下面图像,
已知分类器1的打分结果(如表所示),请计算分类器2的打分结果,以及两个分类器对当前样本的多类支撑向量机损失:
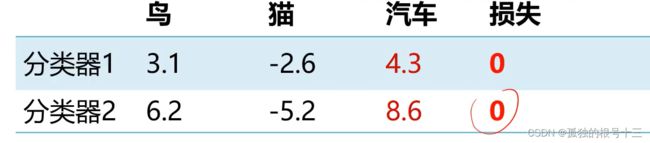
将以上结果套用公式之后,发现损失值都为0,因此W不是唯一的

正则项损失:缓解过拟合

R(W)是一个与权值有关,跟图像数据无关的函数
入:是一个超参数控制着正则损失在总损失中所占的比重
超参数:是学习之前指定的值,而不是学习得到的。超参数一般都会对模型性能有着重要的影响。不如当超参数入等于0时,数据损失成为唯一指标,只要数据分的好就行,相当于退化了,让入等于无穷,这样就不用关注数据分的怎么样,优化函数只用让R(W)等于0就行,根本不用关注数据集的分类性能。正不正确无所谓。

L2正则项: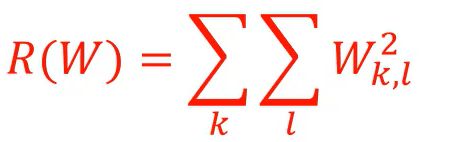
样本:x =[1,1,1,1]
分类器1:w1=[1,0,0,0]
分类器2:W2=[0.25,0.25,0.25,0.25]
分类器输出:
w1转置 x = w1转置x =1
正则损失:
R(w1) =1
R(w2) = 0.25
所以w2总损失小
L2正则损失对大数值权值进行惩罚,喜欢分散权值,鼓励分类器将所有维度的特征都用起来,而不是强烈的依赖其中少数几维特征
上图中的分类器1只要第一项出现损伤,就会出现很严重的后果,如果将所有权值都分散,这样即使某一项有一定的影响最后的结果也不会影响太大!
其他的正则项:
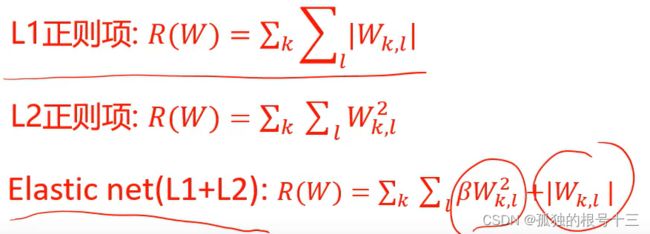
过拟合:”高分低能,只会学习数据集中的,实际跑起来效果却不好“
三.优化算法
参数优化
:参数优化是机器学习的核心步骤之一,它利用损失函数的输出值作为反馈信号来调整分类器参数,以提升分类器对训练样本的预测性能。
优化算法目标:
损失函数L是一个与参数w有关的函数,
优化的目标就是找到使损失函数L达到最优的那组参数w。
直接方法: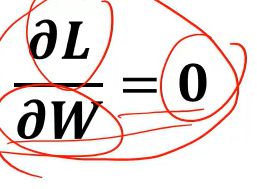
在凸函数下,导数等于0求极值,就为L的最小值。
梯度下降算法
往哪里走:负梯度方向
闭着眼睛,边走边摸。
走多远:步长来决定(学习率),不能太长也不能太短。
梯度下降:利用所有样本计算损失并更新梯度
while True
权值的梯度-计算梯度(损失,训练样本,权值)
权值(更新后)=权值(更新前)-学习率*权值的梯度
当两次权值差异很小时(损失最小)就跳出循环,这个权值就是f(Xi;W)的值
关键:
1.数值法,计算量大,不精确
一维变量 函数求导:注意这里是近似值
、
2.解析法:精确,速度快,导数函数推到容易错

数值梯度有什么作用?
答:求梯度时一般使用解析梯度,而数值梯度
主要用于解析梯度的正确性校验(梯度检查)。
梯度计算:
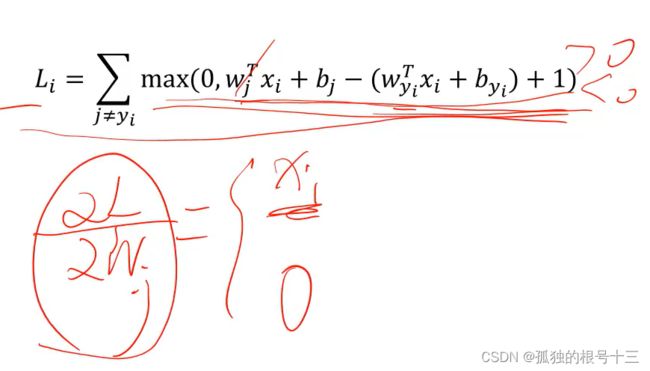
Li对Wj求梯度,如果后面的式子大于0,得到的结果为Xi,如果小于0结果就为0,一次类推,Li对b求梯度则是:后面的式子大于0,结果为1,小于0则结果为0。
随机梯度下降算法
随机梯度下降:每次随机选择一个样本x ;,计算损失并更新梯度
while True
数据-从训练数据采样(训练数据,1)
权值的梯度=计算梯度(损失,数据,权值)
权值=权值-学习率*权值的梯度
快速更新,速度快,单个样本的训练可能会带来很多噪声,不是每次迭代都向着整体最优化方向,但是大量的迭代体现的规律就会朝着最优化的方向走,虽然可能会出现方向偏差,但是下一次的方向就会回来,大体上是正确的方向。
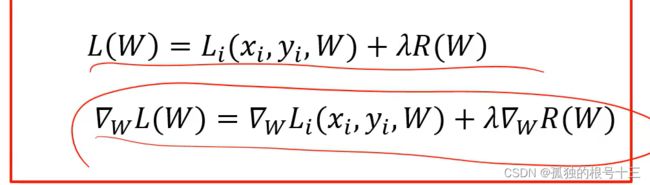
小批量梯度下降算法
小批量随机梯度下降:每次随机选择m(批量的大小)个样本,计算损失并更新梯度
m为另一个超参数,需要自己指定
参数更新=梯度×学习率
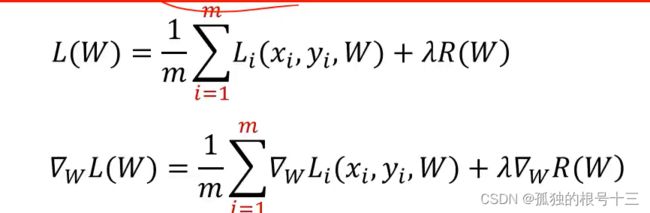
while True
数据一从训练数据采样(训练数据批量大小)
权值的梯度=计算梯度(损失,数据,权值)
权值=权值-学习率*权值的梯度
每次去一定批量大小的数据,将这批数据当作全部的数据去计算梯度再更新权值
通常使用2的幂数作为批量大小,比如每次选取32或64或128个样本
iteration:表示1次迭代,
每次迭代更新1次网给缟构的参数;
batch-size: 1次迭代所使用的样本量;
epoch: 1个epoch表示
过了1遍训练集中的有样本。
四.数据集划分
数据集分为训练集加上测试集加上验证集
训练集:寻找最优分类器
测试集:评估泛化能力
问题:如果模型含有超参数(比如正则化强度),如何找到泛化能力最好的超参数?
训练集用于给定的超参数时分类器参数的学习;
验证集用于选择超参数;
测试集评估泛化能力;
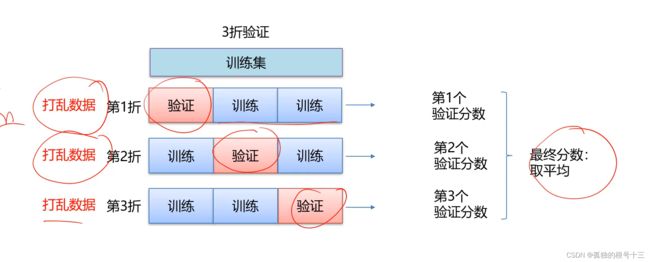
K折交叉验证
问题:如果数据很少,那么可能验证集包含的样本就太少,从而无法在统计上代表数据。
这个问题很容易发现:如果在划分数据前进行不同随机打乱,最终得到的模型性能差别很大,那么就存在这个问题。
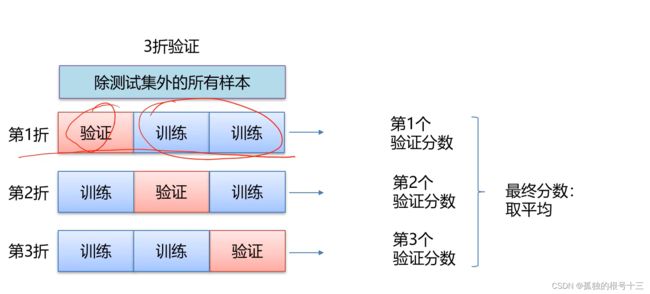
带有打乱数据的重复K折验证
每次取数据的时候将数据都打乱,随机性增强,稳定性越高