为什么神经网络很“深”以及需要如此多的神经元

为什么神经网络很“深”以及需要如此多的神经元

来自 cs231n/cs231n.github.io

为什么神经网络很“深”以及需要如此多的神经元-notion 版本 彩色版

why use more layers

As an aside, in practice it is often the case that 3-layer neural networks will outperform 2-layer nets, but going even deeper (4,5,6-layer) rarely helps much more. This is in stark contrast to Convolutional Networks, where depth has been found to be an extremely important component for a good recognition system (e.g. on order of 10 learnable layers). One argument for this observation is that images contain hierarchical structure (e.g. faces are made up of eyes, which are made up of edges, etc.), so several layers of processing make intuitive sense for this data domain.

The full story is, of course, much more involved and a topic of much recent research. If you are interested in these topics we recommend for further reading:

• Deep Learning book in press by Bengio, Goodfellow, Courville, in particular Chapter 6.4.
• Do Deep Nets Really Need to be Deep?
• FitNets: Hints for Thin Deep Nets

why more neurons

if we have more neurons can express more complicated functions，but easily overfitting

one hidden layer of different nums of hidden neurons:

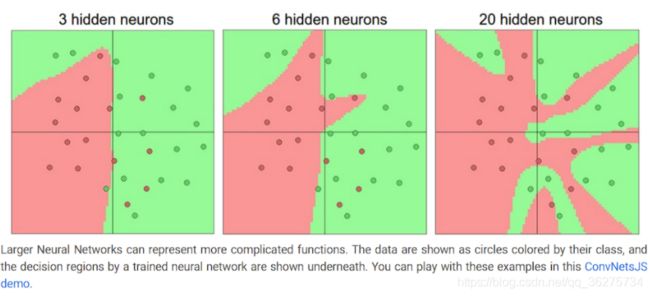
Based on our discussion above, it seems that smaller neural networks can be preferred if the data is not complex enough to prevent overfitting. However, this is incorrect - there are many other preferred ways to prevent overfitting in Neural Networks that we will discuss later (such as L2 regularization, dropout, input noise). In practice, it is always better to use these methods to control overfitting instead of the number of neurons.

The subtle(微妙的) reason behind large networks

The subtle reason behind this is that smaller networks are harder to train with local methods such as Gradient Descent: It’s clear that their loss functions have relatively few local minima, but it turns out that many of these minima are easier to converge to, and that they are bad (i.e. with high loss). Conversely, bigger neural networks contain significantly more local minima, but these minima turn out to be much better in terms of their actual loss. Since Neural Networks are non-convex, it is hard to study these properties mathematically, but some attempts to understand these objective functions have been made, e.g. in a recent paper The Loss Surfaces of Multilayer Networks. In practice, what you find is that if you train a small network the final loss can display a good amount of variance - in some cases you get lucky and converge to a good place but in some cases you get trapped in one of the bad minima. On the other hand, if you train a large network you’ll start to find many different solutions, but the variance in the final achieved loss will be much smaller. In other words, all solutions are about equally as good, and rely less on the luck of random initialization.

The takeaway is that you should not be using smaller networks because you are afraid of overfitting. Instead, you should use as big of a neural network as your computational budget allows, and use other regularization techniques to control overfitting.

总结：smaller networks are harder to train with local methods such as Gradient Descent.

but ,a large network is easy, and rely less on the luck of random initialization. so you should use as big of a neural network as your computational budget allows.

why regularization?

if we want train easily and get low variance , we need larger network in the same time,we don’t want overfitting, wo we need regularization。

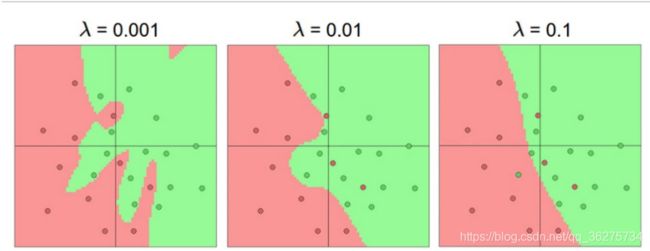
To reiterate, the regularization strength is the preferred way to control the overfitting of a neural network. We can look at the results achieved by three different settings:

The effects of regularization strength: Each neural network above has 20 hidden neurons, but changing the regularization strength makes its final decision regions smoother with a higher regularization. You can play with these examples in this ConvNetsJS demo.