机器学习入门:第十六章 Hopfield神经网络
经过这些年的发展,深度学习慢慢的成为了一种较为流行的算法,从算法的一步步发展来看现在的深度学习算法会觉得深度学习算法不用于已有的神经网络或一些现在流行的算法。虽然深度学习跟神经网络非常的像,但是从原理的本质来看并不相似,传统的神经网络更加的偏向对神经元的模拟,而深度学习算法更是对能量的模拟。进一步在看深度学习算法的话,更容易发现深度学习算法综合了更多方面的内容。
Hopfield神经网络模型
Hopfield神经网络是最早使用能量的概念来搭建网络系统,它的理论基础来源于Ising模型。
Ising模型最早的提出者是Wilhelm Lenz (1920)。后来,他让他的学生Ernst Ising对一维的Ising模型进行求解,但是并没有发现相变现象,因此也没有得到更多物理学家的关注。
随后,著名的统计物理学家Lars Onsager于1944年对二维的ISING模型进行了解析求解,并同时发现了二维ISING模型中的相变现象,从而引起了更多学者的注意。
之后,随着物理学家Landau、Ginzburg等人的努力,人们发现了Ising模型与量子场论之间的联系,并创立了平行的“统计场论”。
Ising模型的提出是为了解释铁磁物质的相变,即磁铁在加热到一定临界温度以上会出现磁性消失的现象,而降温到临界温度以下又会表现出磁性。这种有磁性、无磁性两相之间的转变,是一种连续相变(也叫二级相变)。Ising模型假设铁磁物质是由一堆规则排列的小磁针构成,每个磁针只有上下两个方向(自旋)。相邻的小磁针之间通过能量约束发生相互作用,同时又会由于环境热噪声的干扰而发生磁性的随机转变(上变为下或反之)。涨落的大小由关键的温度参数决定,温度越高,随机涨落干扰越强,小磁针越容易发生无序而剧烈地状态转变,从而让上下两个方向的磁性相互抵消,整个系统消失磁性,如果温度很低,则小磁针相对宁静,系统处于能量约束高的状态,大量的小磁针方向一致,铁磁系统展现出磁性。而当系统处于临界温度T_C的时候,Ising模型表现出一系列幂律行为和自相似现象。
在一个网络中,处于稳定状态时,说明这时系统不容易受到外界的干扰,这种稳定状态下,有一个失真信号从这个系统路过后,这个信号由于受到稳定网络系统的影响,输出值很容易被还原。这个稳定的网络就具备了记忆的功能,它能够还原失真的信号。如何构建一个稳定的网络成为了构建记忆功能的一种方法。
Ising模型中在系统处于一定温度下容易处在一种稳定的状态,如何模拟这种环境呢?假设另外的一种情况,已知方向一直的小磁针后,如何来构建这个Ising模型呢?
Ising模型 的细节推到较为复杂,但有一点跟之前的神经网络的是相似的,每个小磁针之间都存在的互相的关系,就比如在神经网络中, w i j w_{ij} wij中神经网络节点的相互作用一样,在Ising模型中,每在一个温度下维持着一种平衡,而这个平衡中观察到的状态确定了这种平衡状态,因此可以通过观察数据来确定这种相互关系。
把 Ising模型 和神经网络挂上勾是一个较大的创新,它把神经网络的问题和物理能量的问题联系起来,使得神经网络更像物理世界,能量的概念来解决实际中的问题。
也就是在机器学习中,已经获得了一定量的数据后,如何来构建这个神经网络呢?一开始知道Ising模型是一种能量的模型,那能量是怎样的一种表示方式?
把能量模型移植到网络上后,能量行数定义为:
E ( s i ) = − ∑ i j w i j s i s j − ∑ i θ i s i E_{(s_i)}=-\sum_{ij}w_{ij}s_is_j-\sum_i\theta_is_i E(si)=−ij∑wijsisj−i∑θisi
其中 s i s_i si=+1,-1用来表示每个神经元的两种状态:激活和未激活。神经元i到j的连接权重用 w i j w_{ij} wij来表示,两个神经元之间互相的影响参数。 θ i \theta_i θi为阀值常数。
假设训练数据能够是网络达到一种稳定的状态,那通过不断的训练神经元连接参数,就能构建起网络,用如下的规则来调整权重:
w i j = ∑ k = 1 m v k ( i ) v k ( j ) w_{ij}=\sum_{k=1}^mv_k(i)v_k(j) wij=k=1∑mvk(i)vk(j)
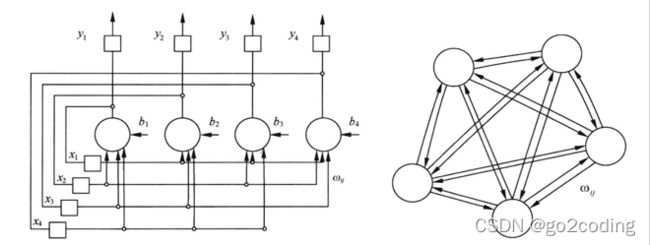
其典型的结构如下:
在Hopfield模型网络中,我们不需要使用误差法不断的通过修正来确定 w i j w_{ij} wij,确定 w i j w_{ij} wij较为容易,比较多的过程在于寻找记忆模型,这需要较多的计算量。
在训练网络的过程中, v k v_k vk就是已知的输入数据,训练结束后,就能得到一组权重 w i j w_{ij} wij。计算 w i j w_{ij} wij的过程如下:
void CalculateWeights(NET* Net)
{
INT i,j,n;
INT Weight;
for (i=0; iUnits; i++) {
for (j=0; jUnits; j++) {
Weight = 0;
if (i!=j) {
for (n=0; nWeight[i][j] = Weight;
}
}
}
通过观察到的数据构建确定这个网络,网络确定了以后就确定了某一种状态。而这个网络相当于记忆了这些观察数据的状态,后面有数据进来以后,通过不断的迭代演变慢慢的变为刚才的记忆状态。
BOOL PropagateUnit(NET* Net, INT i)
{
INT j;
INT Sum, Out;
BOOL Changed;
Changed = FALSE;
Sum = 0;
for (j=0; jUnits; j++) {
Sum += Net->Weight[i][j] * Net->Output[j];
}
if (Sum != Net->Threshold[i]) {
if (Sum < Net->Threshold[i]) Out = LO;
if (Sum > Net->Threshold[i]) Out = HI;
if (Out != Net->Output[i]) {
Changed = TRUE;
Net->Output[i] = Out;
}
}
return Changed;
}
void PropagateNet(NET* Net)
{
INT Iteration, IterationOfLastChange;
Iteration = 0;
IterationOfLastChange = 0;
do {
Iteration++;
if (PropagateUnit(Net, RandomEqualINT(0, Net->Units-1)))
IterationOfLastChange = Iteration;
} while (Iteration-IterationOfLastChange < 10*Net->Units);
}
按照这样的规则一直演化下去,系统将逐渐的收敛到已记忆过的向量中去。在得到了网络后,如果有一个受失真的信号输入后,可通过如下得到记忆的信号:
O U T i = ∑ k = 1 m w i k I k OUT_i=\sum_{k=1}^mw_{ik}I_k OUTi=∑k=1mwikIk,其中 I k I_k Ik为之前输入的信号。
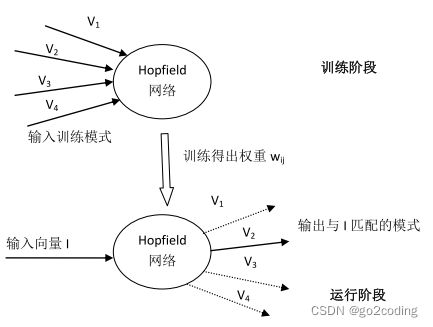
Hopfield神经网络可以通过如上的方式进行构建。Hopfield网络的运行分为两个阶段,它们的输入数粗示意图如下所示:
Hopfield神经网络直接使用了已知的数据进行构建网络,让网络记住之前训练的方式,但并为知道这个网络达到一个什么样的状态。
Hopfield神经网络和前面的神经网络的区别在于,Hopfield神经网络构建的一种记忆型网络,它通过之前的数据建立一种状态,以后输入的数据都会在记忆中的网络找到某一个相似的状态,他适合做信号的还原,而并不能做太多关于数据的判断。
同样的Hopfield神经网络也不能记住数据太多的状态,如果数据的状态较为相似的话很容易做出错误的判断,而后出现了很多基于Hopfield神经网络的基础,改造出了很多的神经网络。Boltzmann波尔兹曼机等网络是较为流行的能量网络。