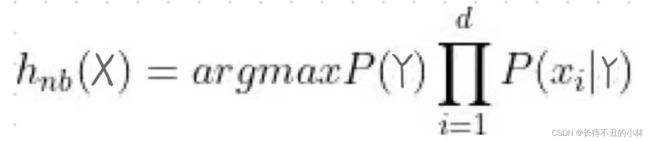朴素贝叶斯（垃圾邮件分类）

目录

一.贝叶斯定理

1.1联合概率分布

1.2条件概率

 1.3条件假设

​编辑二.朴素贝叶斯分类算法原理

 三.拉普拉斯修正

 四.代码实现

1.数据集准备

2.将词表转换成向量

 3.词集模型

4.词袋模型

5.朴素贝叶斯函数

6.朴素贝叶斯分类函数

7.提取单词

8.垃圾邮件测试函数

运行结果：

 五.总结

---

一.贝叶斯定理

1.1联合概率分布

联合概率表示为包含多个条件并且所有的条件都同时成立的概率，记作P(X=a,Y=b)或P(a,b)或P(ab)。比如a是刮风b是下雨，那么既刮风又下雨的概率就是P(a,b)。

联合概率分布就是联合概率在样本空间中的分布情况。

1.2条件概率

条件概率就是A在B条件下发生的概率（记作P(A|B)。

P(A∣B)=P(B)/P(AB)​

 1.3条件假设

条件独立性假设就是各个特征之间互不影响，每个特征都是条件独立的。这一假设使得朴素贝叶斯法变得简单，但是有时候会牺牲一定的分类准确率。由于条件独立那么

P(AB)=P(A)∗P(B)

贝叶斯定理是关于随机事件和 B的条件概率的一则定理。其中 P( A| B)是在 B发生的情况下 A发生的可能性。

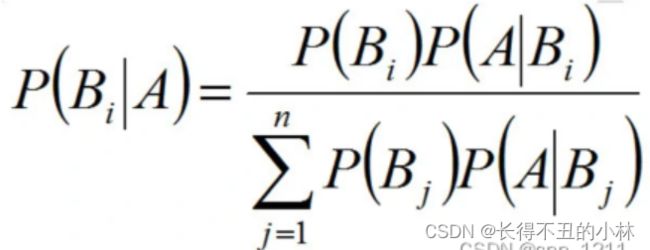
二.朴素贝叶斯分类算法原理

朴素贝叶斯分类算法是基于贝叶斯定理和特征条件独立假设的分类方法。对于给定的训练数据集，首先基于特征条件独立假设学习输入输出的联合概率分布；然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。

朴素：假设的各个特征之间相互独立

相关概念

先验概率P(X)：先验概率是指根据以往经验和分析得到的概率。
后验概率P(Y|X)：事情已发生，要求这件事情发生的原因是由某个因素引起的可能性的大小，后验分布P(Y|X)表示事件X已经发生的前提下，事件Y发生的概率，称事件X发生下事件Y的条件概率。

朴素贝叶斯公式

设有样本数据集D{d1,d2,d3,..,dn}，对应样本数据的特征属性集X={x1,x2,x3,...,xn},类变量为Y={y1,y2,y3,...,yn}，即D可以分为yn个类别。其中x1,x2,x3,...,xn相互独立且随机，则Y的先验概率P1=P（Y），Y的后验概率P2=P（Y|X），由朴素贝叶斯算法可得，后验概率可以由先验概率P1=P（Y）、证据P（X）、类条件概率P（X|Y）计算出：

 朴素贝叶斯基于各特征之间相互独立，在给定类别为y的情况下，上式可以进一步表示为式：

由以上两式可以计算出后验概率为：

其中d为属性数目，xi为第i个属性上的值。

由于对所有的类别P（X）相同，因此最终的朴素贝叶斯表达式就为：

 

 

 三.拉普拉斯修正

拉普拉斯修正：若某个属性值在训练集中没有与某个类同时出现过，则训练后的模型会出现 over-fitting 现象。比如训练集中没有该样例，因此连乘式计算的概率值为0，这显然不合理。因为样本中不存在（概率为0），不代该事件一定不可能发生。所以为了避免其他属性携带的信息，被训练集中未出现的属性值“ 抹去” ，在估计概率值时通常要进行“拉普拉斯修正”。
令 N 表示训练集 D 中可能的类别数，  表示第i个属性可能的取值数，则贝叶斯公式可修正为：

 四.代码实现

1.数据集准备

将数据集分成2类，都以txt的方式储存

2.将词表转换成向量

def loadDataSet():
    postingList = [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                   ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                   ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                   ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                   ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                   ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0, 1, 0, 1, 0, 1]  # 1代表侮辱性文字，0代表正常言论
    return postingList, classVec
 
 
# 创建词汇表
def createVocabList(dataSet):
    vocabSet = set([])  # 创建一个空集
    for document in dataSet:
        vocabSet = vocabSet | set(document)  # |表示求并操作
    return list(vocabSet)  # 返回一个不重复的列表
 
 
# 输出文档向量
def setOfwords2Vec(vocabList, inputSet):
    returnVec = [0] * len(vocabList)  # 创建一个等长向量并设置为0
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1  # 若出现了单词表中的单词，则将对应值设置为1
        else:
            print("单词:%s 不存在!" % word)
    return returnVec
 
 
# 测试函数效果
 
# 创建实验样本
listPosts, listClasses = loadDataSet()
print('数据集\n', listPosts)
# 创建词汇表
myVocabList = createVocabList(listPosts)
print('词汇表:\n', myVocabList)
# 输出文档向量
print(setOfwords2Vec(myVocabList, listPosts[5]))

 3.词集模型

为输入的邮件构造单词集合

#词集模型
def setOfWord2Vec(vocabList,inputSet):
    returnVec=zeros(len(vocabList))
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)]=1
        else:
            print("这个单词不在所有的单词向量里面") 
    return  returnVec

4.词袋模型

#词袋模型
def bagOfword2VecMN(vocabList,inputSet):
    returnVec=[0]*len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)]+=1
    return  returnVec

5.朴素贝叶斯函数

#朴素贝叶斯训练函数
def trainB0(trainMatrix,trainCategory):
    numTrainDocs=len(trainMatrix)
    numwords=len(trainMatrix[0])
    #对于category为0,1 才可以使用sum
    pAbusive=sum(trainCategory)/float(numTrainDocs)
    p0Num=ones(numwords)
    p1Num=ones(numwords)

    p0Denom=2.0
    p1Denom=2.0
    for i in range(numTrainDocs):
        if trainCategory[i]==1:
            p1Num+=trainMatrix[i]
            p1Denom+=sum(trainMatrix[i])
        else:
            p0Num+=trainMatrix[i]
            p0Denom+=sum(trainMatrix[i])

    p1Vect=log(p1Num/p1Denom)
    p0Vect=log(p0Num/p0Denom)
    return p0Vect,p1Vect,pAbusive

6.朴素贝叶斯分类函数

#朴素贝叶斯分类函数
def classifyNB(vec2Classify,p0Vec,p1Vec,pClass1):
    p1=sum(vec2Classify*p1Vec)+log(pClass1)
    p0=sum(vec2Classify*p0Vec)+log(1-pClass1)
    if p1>p0:
        return 1
    else:
        return 0

7.提取单词

#将输入的文本字符串分割成单词list
def textParse(bigString):
    listOfTokens=re.split(r'\W*',bigString)
    return [tok.lower() for tok in listOfTokens if len(tok)>2]

8.垃圾邮件测试函数

def spamTest():
    docList=[]
    classList=[]
    fullText=[]

    filenameList1=listdir("email/train")
    for name in filenameList1:
        wordList=textParse(open("email/train/"+name).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(1)

    filenameList2=listdir("email/test")
    for name in filenameList2:
        wordList = textParse(open("email/test/"+name).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(0)

    vocabList=createVocabList(docList)
    trainingSet=list(range(len(docList)))

    testSet=[]
    for i in range(int(0.2*len(docList))):
        randIndex=int(random.uniform(0,len(trainingSet)))
        testSet.append(trainingSet[randIndex])
        del(trainingSet[randIndex])
    trainMat=[]
    trainClasses=[]
    for docIndex in trainingSet:
        trainMat.append(setOfWord2Vec(vocabList,docList[docIndex]))
        trainClasses.append(classList[docIndex])

    p0V,p1V,pSpam=trainB0(array(trainMat),array(trainClasses))
    errorCount=0

    for  docIndex in testSet:
        wordVector=setOfWord2Vec(vocabList,docList[docIndex])
        if classifyNB(array(wordVector),p0V,p1V,pSpam)!=classList[docIndex]:
            errorCount+=1
    print (r"垃圾邮件准确率:",float(errorCount/float(len(testSet))))

运行结果：

 五.总结

最后准确率只有0.73，不算太高也不算太低，对于该模型来说想要提高准确率，下次使用的应该是具有独立性比较高的数据集，只有在完全独立的时候才能满足公式算出来的概率。