sklearn学习02——SVM

---

前言

本篇给出sklearn中 SVM（支持向量机）的一些常用模型的实现，线性分类问题一般可用 线性SVM模型来解决；非线性分类问题可以使用多项式SVM、高斯核SVM这两种模型解决。

---

一、线性SVM

1.1、算法原理

回顾一下线性SVM的分类思想：线性可分支持向量机（SVM）也是一种线性二分类模型，也需要找到满足 以下约束条件的划分超平面，即（w, b），由于能将样本分开的超平面可能有很多，SVM进一步希望找到离个样本都比较远的划分超平面。

关于寻找 最优超平面的问题，我们转化到数学表达上，就是：寻找使得几何间隔最小的那个超平面。几何间隔就是直观上的点到超平面的距离。
之后的目标函数推导、求最优解的方法这里不再讲解（可以参考西瓜书/南瓜书的第六章——支持向量机）

1.2、代码实现

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm

data = np.array([
    [0.1, 0.7],
    [0.3, 0.6],
    [0.4, 0.1],
    [0.5, 0.4],
    [0.8, 0.04],
    [0.42, 0.6],
    [0.9, 0.4],
    [0.6, 0.5],
    [0.7, 0.2],
    [0.7, 0.67],
    [0.27, 0.8],
    [0.5, 0.72]
])
label = [1] * 6 + [0] * 6
x_min, x_max = data[:, 0].min() - 0.2, data[:, 0].max() + 0.2
y_min, y_max = data[:, 1].min() - 0.2, data[:, 1].max() + 0.2
xx, yy = np.meshgrid(np.arange(x_min, x_max, 0.002),
                     np.arange(y_min, y_max, 0.002)) # meshgrid如何生成网格
model_linear = svm.SVC(kernel='linear', C = 0.001)
model_linear.fit(data, label) # 训练
Z = model_linear.predict(np.c_[xx.ravel(), yy.ravel()]) # 预测
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap = plt.cm.ocean, alpha=0.6)
plt.scatter(data[:6, 0], data[:6, 1], marker='o', color='r', s=100, lw=3) 
plt.scatter(data[6:, 0], data[6:, 1], marker='x', color='k', s=100, lw=3)
plt.title('Linear SVM')
plt.show()

分类效果如下图：

二、核函数和非线性SVM

2.1、从线性可分到线性不可分

支持向量机是一种二分类模型，他的目的是寻找一个超平面对样本进行分割，分割的原则是间隔最大化，最终转换为一个凸二次规划问题来求解，而由简至繁的模型包括：

• 当训练样本线性可分时，通过硬间隔最大化，学习一个线性可分支持向量机
• 当训练样本近似线性可分时，通过软间隔最大化，学习一个线性支持向量机
• 当训练样本线性不可分时，通过核技巧和软间隔最大化，学习一个非线性支持向量机

2.2、核函数

原始空间向特征空间的映射需要借助映射函数 Ψ(x)。例如对于数据点 xi，映射到特征空间就变成了Ψ(xi)。而SVM的一大巧妙之处就是映射后的特征空间数据点内积的计算等价于低维空间数据点在映射函数对应的核函数中计算。这大大降低了运算量，因为有的时候高维空间的计算很复杂。

2.2.1、多项式核函数

内部实现：

• 对传入的样本数据点添加多项式项；
• 新的样本数据点进行点乘，返回点乘结果；
• 多项式特征的基本原理：依靠升维使得原本线性不可分的数据线性可分；
• 升维的意义：使得原本线性不可分的数据线性可分；

代码实现：

plt.figure(figsize=(16, 15))
 
for i, degree in enumerate([1, 3, 5, 7, 9, 12]):
    # C: 惩罚系数，gamma: 高斯核的系数
    model_poly = svm.SVC(C=0.0001, kernel='poly', degree=degree) # 多项式核
    model_poly.fit(data, label)
    # ravel - flatten
    # c_ - vstack
    # 把后面两个压扁之后变成了x1和x2，然后进行判断，得到结果在压缩成一个矩形
    Z = model_poly.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    plt.subplot(3, 2, i + 1)
    plt.subplots_adjust(wspace=0.4, hspace=0.4)
    plt.contourf(xx, yy, Z, cmap=plt.cm.ocean, alpha=0.6)
 
    # 画出训练点
    plt.scatter(data[:6, 0], data[:6, 1], marker='o', color='r', s=100, lw=3)
    plt.scatter(data[6:, 0], data[6:, 1], marker='x', color='k', s=100, lw=3)
    plt.title('Poly SVM with $\degree=$' + str(degree))
plt.show()

2.2.2、高斯核函数

怎么分类非线性可分的样本的分类？

采用的方法：按一定规律统一改变样本的特征数据得到新的样本，新的样本按新的特征数据能更好的分类，由于新的样本的特征数据与原始样本的特征数据呈一定规律的对应关系，因此根据新的样本的分布及分类情况，得出原始样本的分类情况。

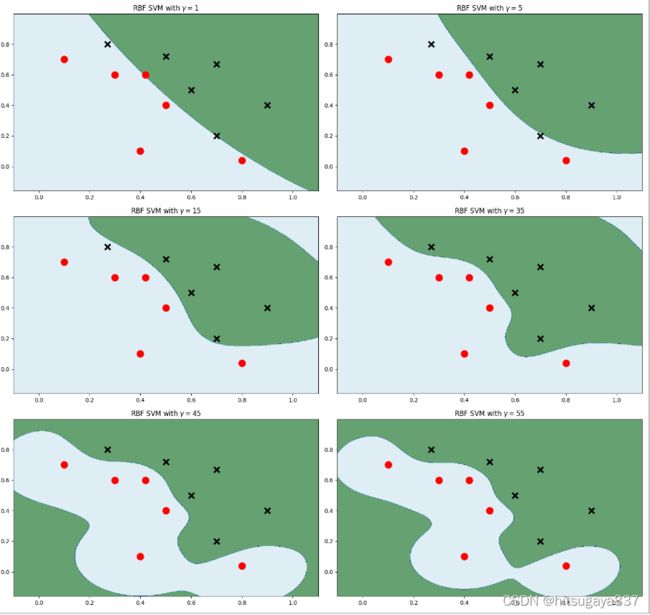
代码实现：

plt.figure(figsize=(16, 15))
 
for i, gamma in enumerate([1, 5, 15, 35, 45, 55]):
    # C: 惩罚系数，gamma: 高斯核的系数
    model_rbf = svm.SVC(kernel='rbf', gamma=gamma, C= 0.0001).fit(data, label)
 
    # ravel - flatten
    # c_ - vstack
    # 把后面两个压扁之后变成了x1和x2，然后进行判断，得到结果在压缩成一个矩形
    Z = model_rbf.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)

    plt.subplot(3, 2, i + 1)
    plt.subplots_adjust(wspace=0.4, hspace=0.4)
    plt.contourf(xx, yy, Z, cmap=plt.cm.ocean, alpha=0.6)
 
    # 画出训练点
    plt.scatter(data[:6, 0], data[:6, 1], marker='o', color='r', s=100, lw=3)
    plt.scatter(data[6:, 0], data[6:, 1], marker='x', color='k', s=100, lw=3)
    plt.title('RBF SVM with $\gamma=$' + str(gamma))
plt.show()

2.3、测试不同SVM在Mnist数据集上的分类情况

代码如下：

import sys
from pathlib import Path
curr_path = str(Path().absolute()) # 当前文件所在绝对路径
parent_path = str(Path().absolute().parent) # 父路径
sys.path.append(parent_path) # 添加路径到系统路径

from Mnist.load_data import load_local_mnist
from sklearn import svm

(X_train, y_train), (X_test, y_test) = load_local_mnist(normalize=True,one_hot=False)

# 截取部分数据，否则程序运行可能超时
X_train, y_train= X_train[:2000], y_train[:2000] 
X_test, y_test = X_test[:200],y_test[:200]

# C:软间隔惩罚系数
C_linear = 100
model_linear = svm.SVC(C = C_linear, kernel='linear').fit(X_train,y_train) # 线性核
print(f"Linear Kernel 's score: {model_linear.score(X_test,y_test)}")
for degree in range(1,10,2):
    model_poly = svm.SVC(C=100, kernel='poly', degree=degree).fit(X_train,y_train) # 多项式核
    print(f"Polynomial Kernel with Degree = {degree} 's score: {model_poly.score(X_test,y_test)}")

for gamma in range(1,10,2):
    gamma = round(0.01 * gamma,3)
    model_rbf = svm.SVC(C = 100, kernel='rbf', gamma = gamma).fit(X_train,y_train) # 高斯核
    print(f"Polynomial Kernel with Gamma = {gamma} 's score: {model_rbf.score(X_test,y_test)}")

对比结果：