一文看懂数据分析各种图形(箱型图、数据分布图、线性回归图、相关关系图)(阿里天池)
1、箱形图
1.1箱型图的定义
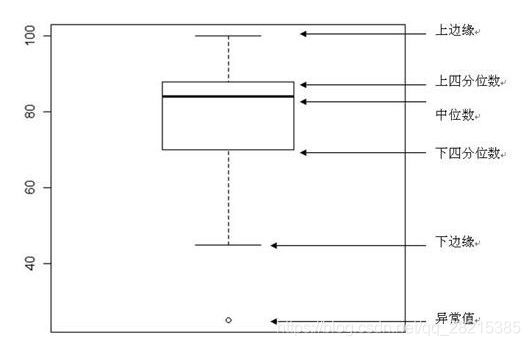
箱型图(Boxplot)也称箱须图(Box-whisker Plot)、盒式图或箱线图,是利用数据中的五个统计量:最小值、上四分位数、中位数、下四分位数与最大值来描述数据的一种统计图。它能够直观地显示数据的异常值,分布的离散程度以及数据的对称性。
中位数:数据按从小到大顺序排列后的处于中间位置的值,如果序列是偶数个,则是中间两个数的平均值;
下四分位数Q1:位于数据序列25%位置处的数;
上四分位数Q3:位于数据序列75%位置处的数;
四分位间距IQR:即 IQR = Q3-Q1;
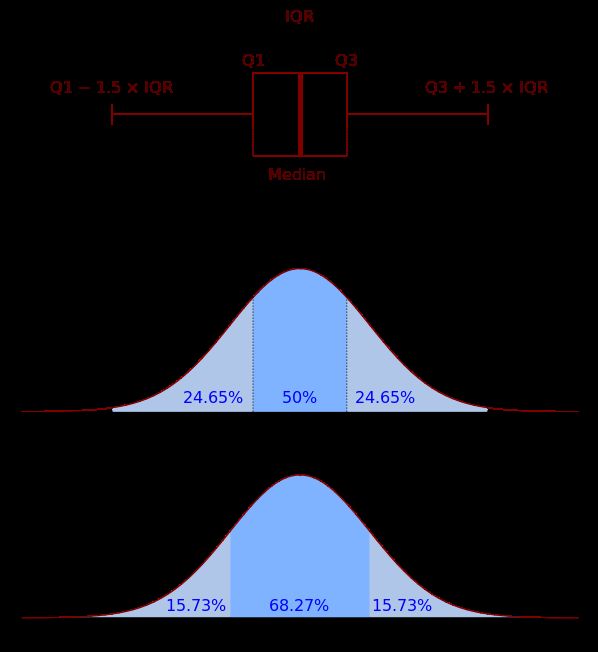
下边缘:= Q1 – 1.5 *IQR;
上边缘:= Q3 + 1.5 *IQR;
可能有人会有这样的疑问:上下边缘都是加减IQR,为什么图中的虚线长度会不一样?
其实下边缘的确定是依据大于Q1-1.5*IQR的最小值,所以除非刚好有值等于Q1-1.5*IQR,否则实际的下边缘是要比Q1-1.5*IQR大的。同理,上边缘就是小于Q3 + 1.5 *IQR的最大值。所以大多数情况下,上下虚线是不等长的。而是-2.698~2.698![]() 的长度,略小于
的长度,略小于![]() .
.
1.2箱型图的特征
1.直观地观察到异常值,如果数据存在离群点,即位于上下边缘区域之外,以圆点的形式表示
2.当箱型图很短时,意味着很多数据多集中分布在很小的范围内
3.当箱型图很长时,意味着数据分布比较离散,数据间的差异比较大
4.当中位数接近底部时,说明大部分的数据值比较小
5.当中位数接近顶部时,说明大部分的数据值比较大
6.中位数所处的高低位置能反映数据的偏斜程度
7.如果上下虚线比较长,说明上下四分位数之外的数据变化比较大,整体数据的方差和标准偏差也比较大
8.箱型图的上下边缘并非最大值或最小值
1.3箱型图的缺点
1.箱型图虽然能显示出数据的分布偏态,但是不能提供关于数据分布偏态和尾重程度的精确度量;
2.对于批量较大的数据批,箱线图反映的形状信息更加模糊;
3.用中位数代表总体平均水平有一定的局限性。
所以,应用箱线图最好结合其它描述统计工具如均值、标准差、偏度、分布函数等来描述数据批的分布形状。
1.4箱型图的python实现
fig = plt.figure(figsize=(4, 6)) # 指定绘图对象宽度和高度
sns.boxplot(train_data['V0'],orient="v", width=0.5) #第一个参数为数据,orient为朝向,width为线宽
2、数据分布图
2.1 直方图
2.2.1 定义
直方图(Histogram),又称质量分布图,是一种统计报告图,由一系列高度不等的纵向条纹或线段表示数据分布的情况。 一般用横轴表示数据类型,纵轴表示分布情况。
直方图是数值数据分布的精确图形表示。 这是一个连续变量(定量变量)的概率分布的估计,并且被卡尔·皮尔逊(Karl Pearson)首先引入。它是一种条形图。 为了构建直方图,第一步是将值的范围分段,即将整个值的范围分成一系列间隔,然后计算每个间隔中有多少值。 这些值通常被指定为连续的,不重叠的变量间隔。 间隔必须相邻,并且通常是(但不是必须的)相等的大小。
直方图也可以被归一化以显示“相对”频率。 然后,它显示了属于几个类别中的每个案例的比例,其高度等于1。
2.2.2直方图的python实现
plt.figure(figsize=(10,5)) #设置图形的大小
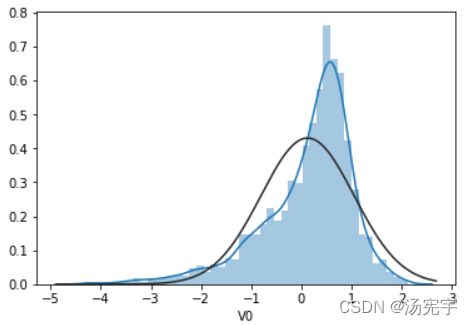
sns.distplot(train_data['V0'],fit=stats.norm)
程序解析:displot()集合了matplotlib的hist()与核函数估计kdeplot的功能,增加了rugplot分布观测条显示与利用scipy库fit拟合参数分布的新颖用途。默认情况下,它会画一个直方图,并且做一个核密度估计(KDE)。具体用法如下:
seaborn.distplot(a, bins=None, hist=True, kde=True, rug=False, fit=None, hist_kws=None, kde_kws=None, rug_kws=None, fit_kws=None, color=None, vertical=False, norm_hist=False, axlabel=None, label=None, ax=None)
2.2 Q-Q图
2.2.1定义
QQ图是一种散点图,对应于正态分布的QQ图,就是由标准正态分布的分位数为横坐标,样本值为纵坐标的散点图。要利用QQ图鉴别样本数据是否近似于正态分布,只需看QQ图上的点是否近似地在一条直线附近,图形是直线说明是正态分布,而且该直线的斜率为标准差,截距为均值,用QQ图还可获得样本偏度和峰度的粗略信息。
如果样本是按正态分布的,那么f(x)即是一个正态分布的概率密度函数。根据正态分布的特性,我们又可以推导出对应的标准正态分布的概率密度函数:![]()
其中m为样本均值,std为样本标准差。
设标准正态分布的概率密度函数为 y= f(n),既然这些值一一对应,则有:
(x-m)/std=n
即:x=n*std+m
这是一条斜率为样本标准差,截距为m的直线,就是在q-q图中代表着正态分布的直线。
可见第一个和第二个图符合正态分布性较差,第三个图基本符合正态分布。
2.2.2 Q-Q图的python实现
# 通过比较数据和正态分布的分位数是否相等来判断数据是不是符合正态分布
res = stats.probplot(train_data['V0'], plot=plt)
3、线性回归关系图
3.1定义
线性回归关系图会画出关于x、y两个变量的散点图,同时用数据拟合一个y ~ x的模型出来,并将对应的直线和95%的置信区间绘制出来。
3.2 线性回归关系的python实现
sns.regplot(x='V0', y='target', data=train_data,
scatter_kws={'marker':'.','s':3,'alpha':0.3},
line_kws={'color':'k'});
4、热力图
4.1热力图的定义
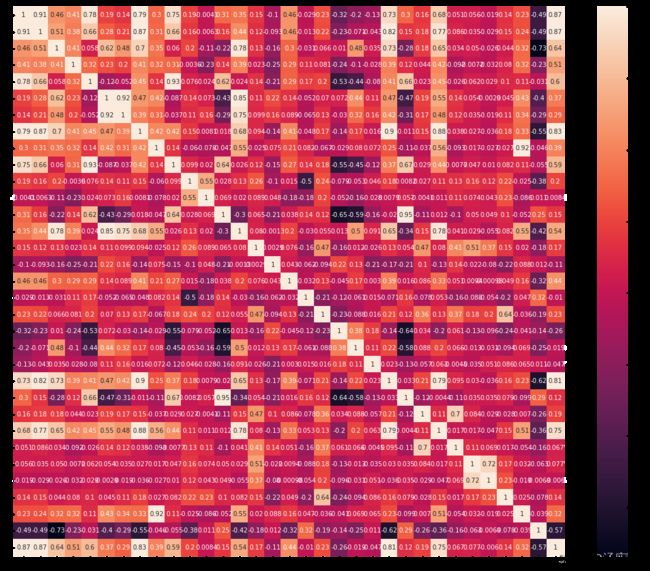
热力图(heatmap)可通过颜色深浅变化,优雅的展示数据的差异。热图还可以用于展示不同指标、不同样本等之间的相关性。
此时颜色代表的就是相关系数的大小。所以可以看到自己和自己的相关系数是1,也就是最深的蓝色。约接近白色说明相关性越弱,偏蓝(正相关)或者偏红(负相关)则代表相关性强。当然在相关性的计算中除了相关系数以外,我们还会看pvalue是否显著。如果我们想要把pvalue表示在图中,可以在格子上添加*号或者具体的数值。同时因为这里可以看到其实不同的两个指标之间的关系是被重复展现了2次,比如symboling与normalized-losses(最上面一行的第二个格子,和从上往下的第二行的第一个格子),因此有时候我们只展现一半即对角线以上或以下的一半图形。
4.2 热力图的python实现
ax = sns.heatmap(train_corr, vmax=.8, square=True, annot=True)#画热力图 annot=True 显示系数