【cs231n】lecture 3损失函数和优化

3.1 损失函数

损失函数的概念理解：

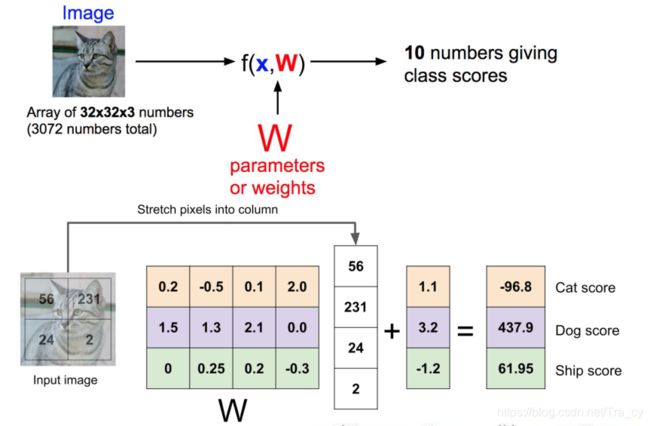
在线性分类中，W的每一行对应一个分类模板，它给出图片所属类别的可能的得分，得分越高说明该图片中的物体属于这一类别的可能性越大，因此我们需要选择一个分类效果最优的W，W来自于数据集的训练。
损失函数就是用来度量某个W好坏的，输入为W，得到一个得分，定量地估计W的好坏，这个函数即为损失函数。

数学公式表示：

上图中第一个公式为给定的数据集，$x_i$表示一张输入的图片，对于计算机而言，就是像素点的一个向量，$y_i$表示图片所对应的类别，即label。第二个公式中，$f(x_i,W)$计算不同分类类别的分值。$L_i(f(x_i,W),y_i)$表示第i个图片的损失函数，L是整体的一个损失函数，这个函数是所有图片损失函数的一个平均值。

多分类SVM（Support Vector Machine）

课件上给出的SVM损失函数的公式如下:

下面给出SVM损失函数的一般定义：
这里，我们将分值简写为$s$，即针对第j个类别的得分为$s_j=f(x_i,W{)}_j$。针对第i个数据的多类SVM的损失函数定义如下：

举例用一个例子演示公式是如何计算的。假设有3个分类，并且得到了分值$s=[13,-7,11]$，其中第一个类别是正确类别，即$y_i=0$。同时假设$\Delta$是10。上面的公式是将所有不正确分类$(j\ne y_i)$，加起来，所以我们得到两个部分：

可以看到第一个部分结果是0，这一对类别分数和标签的损失值是0，这是因为正确分类的得分13与错误分类的得分-7的差为20，高于边界值10。而SVM只关心差距至少要大于10，更大的差值还是算作损失值为0。第二个部分计算[11-13+10]得到8。虽然正确分类的得分比不正确分类的得分要高（13>11），但是比10的边界值还是小了，分差只有2，这就是为什么损失值等于8。

简而言之，SVM的损失函数想要正确分类类别$y_i$的分数比不正确类别分数高，而且至少要高$\Delta$。如果不满足这点，就开始计算损失值。

整体的损失函数是所有$L_i$的值求和取平均值。

上面所说的max(0,-)函数，我们通常称为折叶损失函数（hinge loss），图像如下图所示

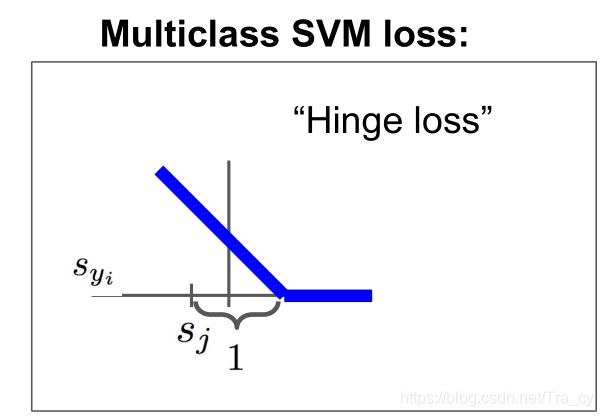
x轴表示$s_{y_i}$，是图像在真实分类上的得分，y轴是损失，随着真实分类分数的提高，损失会线性下降，直到分数超过了一个阈值，损失函数就会是0，表示我们已经对样本成功地分了类。

思考：
1、SVM损失函数可能的最小值是0，最大值是无穷大；
2、当计算所得的所有样本的$s$值都很接近的时候，损失函数的值接近于$N-\Delta$，这可以作为一种调试策略，在训练之前预想损失函数的值，第一次迭代损失函数的值不应该接近于$N-\Delta$，否则程序可能有问题。
3、如果对于SVM的所有分数求和，包括正确的分类，那么，损失函数会增加$\Delta$，但是一般我们认为损失函数为0是最好的，所以一般我们求和的时候不包括正确的分类。
4、如果对于每一项$L_i$，我们使用的是求平均而不是求和，结果不会改变，只是损失函数缩小了一个倍数，对于结果没有什么影响。
5、如果我们改变损失函数的公式，在max上加一个平方，这将称为另外一个分类算法，从一个线性的变为一个更强烈的算法，有的时候平方max的方法可能会更好。
6、当我们找到一个W，使得某一项$L_i$的损失函数为0，那么这个W是最优的，我们对这个W进行成倍数缩放，这一项的损失函数值仍然为0。

正则化

正则化的概念及原因：
简单来说，正则化是一种为了减小测试误差的行为(有时候会增加训练误差)。我们在构造机器学习模型时，最终目的是让模型在面对新数据的时候，可以有很好的表现。当你用比较复杂的模型比如神经网络，去拟合数据时，很容易出现过拟合现象(训练集表现很好，测试集表现较差)，这会导致模型的泛化能力下降，这时候，我们就需要使用正则化，降低模型的复杂度。

刚开始不太能理解这个点，感觉比较抽象，后来在网上看到这样一个例子就理解了：
假设我们的模型就是一只蚊子，我们要训练它去模拟空中的一些点的整体路径：我们空中的点也分为训练集和测试集，蚊子去学习训练集的路径，然后闭上眼睛，按照自己学习到的那个路径去预测测试集的点是否在路径上。
蚊子飞行游戏：
首先，蚊子自以为聪明灵活，自由自在地飞翔，它轻轻松松地经过了所有训练集的点，很明显，训练集满分！每个点都完美经过了！
接下来给它蒙上眼睛，看看它能否经过预测集的点。很可惜，自以为聪明的蚊子按照自己学习到的复杂的路径上上下下，却几乎一个点都没预测对。。。这就是over fitting！因为每个数据都带有随机性，你不能学的太认真，正所谓“你认真，就输了”。
但是蚊子也没办法，它也不知道怎么“不认真”，于是我们来想办法，强迫它别那么较真。我们想了个办法：
我们设计了一个 挂坠，给蚊子挂上，这样蚊子飞起来就有些费劲了，没办法自由自在上蹿下跳地飞行了，这也就是大家常常听说的“惩罚项”，因为身上有个挂坠，你蚊子上下飞就很费力，于是限制了蚊子的乱动。果真，蚊子的飞行没有那么“皮”了，它怎么省力怎么飞，每次看到新的点，它只是忘那个方向偏一点，不能偏太多，因为下一个点可能方向又变了，那得累死它，所以它在挂坠的限制下，会努力找一个中间的位置，让它不费力，又能尽可能拟合训练点。负重飞行的成绩就好很多了。
这个**“挂挂坠”**，就是正则化。

正则化，就是给损失函数加一个正则化项，相当于给它一个惩罚。标准的损失函数由两部分组成：损失项和惩罚项。超参数$\lambda$是用来平衡两项的。

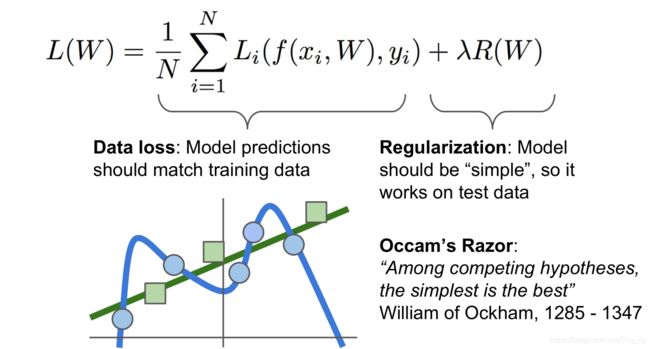常用的有L1、L2正则化以及二者的一种结合。  L1的惩罚项：对每个W求所有特征系数绝对值的和。 L2的惩罚项：对每个W求所有特征系数的平方和。 整体的惩罚项：将每个W的惩罚项相加。

例子：
假设输入向量x=[1,1,1,1]，两个权重向量$w_i=[1,0,0,0]$，$w_2=[0.25,0.25,0.25,0.25]$，可得$w_1^{T}x=w_2^{T}x=1$,两个权重向量都得到同样的内积，但是$w_1$的L2惩罚是1，而$w_2$的L2惩罚是0.25。因此，根据L2惩罚来看，$w_2$更好，因为它的正则化损失更小。

从直观上来看，这是因为$w_2$的权重值更小且更分散。既然L2惩罚倾向于更小更分散的权重向量，这就会鼓励分类器最终将所有维度上的特征都用起来，而不是强烈依赖其中少数几个维度。

Softmax Classifier (Multinomial Logistic Regression)

多类别的SVM损失函数中，我们没有对于每个类别的得分做出任何解释，只是对每个类别给出一个分数，并希望正确类别的得分不应该低于错误类别的得分。但是对于Multinomial Logistic Regression损失函数，我们将赋予这些得分一些额外的含义。并且用这些分数，针对我们的类别去计算概率分布，这样对于所有类别，我们都有了相应的概率。

公式P求出来的是输入$x_i$属于类别K的概率，s是类别的得分，我们希望真实类别所求得的概率比较高并接近于1，所以损失函数就是真实类别概率的对数再取负值，当概率为1时，损失为0，概率越接近0，损失越大。

例子：

思考：
1、softmax损失函数的最小值是0，最大值是无穷。
2、如果所有的s都很小并接近于0，那么损失函数的值为-log（1/N），这个也可以作为一种纠错机制。

多分类SVM和softmax对比：
二者都属于线性分类问题，不同的是两种方式如何解释得分s的问题。SVM研究的是正确分类和不正确分类的分值的边际；而对于softmax，是计算一个概率分布。

过程回顾：
已有数据集：（x，y）；我们使用线性分类器来获得一些分数函数：s=f(x;W)（eg. =Wx），根据我们的输入x计算分数s；然后我们使用损失函数（softmax、SVM或者其他损失函数）来定量地计算模型的预测与真实值之间的差距；然后我们会增加损失函数（正则化），在训练数据之间进行权衡，选择一个更简单的模型。这就是一个监督学习的过程。

3.2 优化（Optimization）

优化的理解：
上面的讨论中一直在说W，对于如何找到一个最好的W，就是我们所说的优化的问题。一般是从某个方案出发，逐步迭代，不断优化。

多元函数下的导数概念就是梯度，梯度就是偏导数组成的向量，这是一个很重要的概念，计算梯度的方法：
有限差分法

在W的每个方向上增加一小个步长，计算这个方向上的偏导，每个方向都采取相同的做法，这种方法对于大规模的数据，计算量达，速度慢。
损失函数是关于W的函数，所以利用微积分公式会大大提高效率。

梯度下降算法：
先初始化W为随机值，计算损失和梯度，然后向梯度相反的方向更新权重值（梯度指向函数的最大增加方向），我们向梯度减小的方向前进一小步，然后一直重复，最后网络会收敛。这里的步长是一个超参数，告诉我们每次计算梯度时，向那个方向前进多长的距离，这个步长也叫学习率，找到合适的学习率，是训练模型时第一步需要做的工作。

随机梯度下降算法：
计算所有样本的损失和梯度的计算量太大，一般每次训练，取一小部分训练样本（batch），一般取2的n次幂，如32，64，128，利用每一个batch来估计误差总和和实际梯度，因为是随机的，所以可以把这个数据看作是对真实数值期望的一种蒙特卡洛估计。

3.3 图像的特征

拿到图片之后，计算图片的各种特征代表，例如：计算与图片形象有关的数值，然后将不同的特征向量合到一块儿，得到图像的特征表述，然后在输入线性分类器，而不是原始像素直接输入分类器。