基于主成分分析的支持向量机入侵检测系统

申明： 未经许可，禁止以任何形式转载，若要引用，请标注链接地址。 全文共计4018字，阅读大概需要3分钟
更多学习内容， 欢迎关注我的个人公众号：不懂开发的程序猿

学习目标：

一、基于主成分分析的支持向量机入侵检测系统

学习内容：

本文针对Knowledge Discovery in Databases Cup’99（KDD）数据集评估了支持向量机（SVM）不同核的性能，并比较了检测精度、检测时间。通过采用将高维数据集缩减为低维数据集的主成分分析（PCA）来减少检测时间。本研究进行的实验表明，支持向量机的高斯径向基函数核具有较高的检测精度。

A. 数据集分析

数据集：KDD
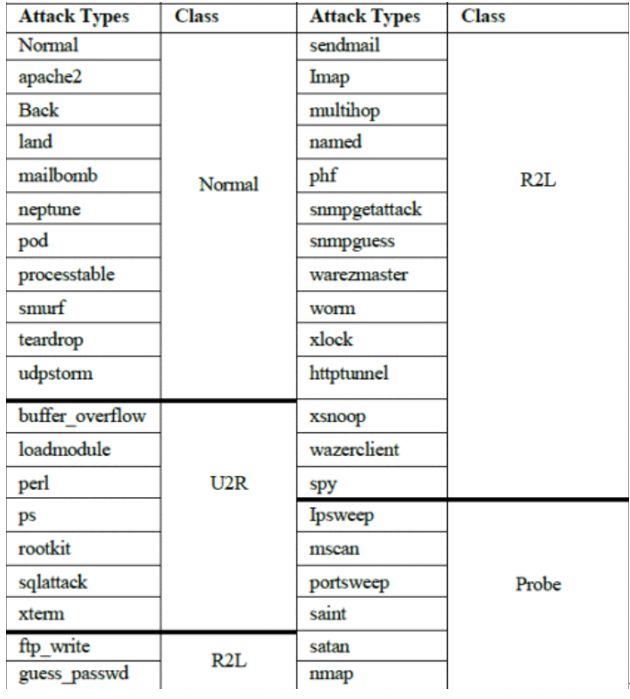
整个 KDDCup‘99 数据集由 4,898,431 条记录组成，其中每条记录包含 41 个特征。我们仅使用 KDDdataset 的 10% 部分用于训练目的和整个 KDDdataset 用于测试。此外，10% KDDCup’99 数据包含 494,069 条记录（每条记录包含 41 个特征），并分为 4 种类型的攻击，探测、拒绝服务 (DOS)、用户到根 (U2R)、根到本地(R2L)

B. 主成分分析 (PCA)–降维

PCA 是通过消除包含最大计算成本的高维空间中不太重要的属性，从而将更有用和相关的属性投影到低维子空间中来实现的。让我们考虑一个长度为“m”且经过“n”次检查的向量，那么给定的数据集可以由矩阵 X 表示为
$$X_{(}m\ast n)=[X_1,X_2,X_3,...,X_n]\text{\hspace{1em}(1)}$$
等式1表明 X 的每一列都是一个向量

等式2显示平均均值( μ )对于每个向量
$$\mu =\frac{1}{n}{\Sigma }_{i-1}^n{X}_{ij}\text{\hspace{1em}(2)}$$
给定向量与其均值的变化由称为偏差的度量给出，由公式3给出
$$\Phi =X_i-\mu \text{\hspace{1em}(3)}$$
两个变量之间的关系程度通过称为协方差的度量来衡量。如果协方差为正，则称这两个变量正相关，如果协方差为负，则称这两个变量负相关，如果协方差为零，则称数据不相关。所以从协方差矩阵中，我们可以实现数据的传播。协方差矩阵( Σ )构造如等式（4）中所示
$$\sum =\frac{1}{n-1}{\Sigma }_{i=1}^n{\Phi }_i{\Phi }_i^T=\frac{1}{n-1}{\Sigma }_{i=1}^n(X_i-\mu )(X_i-\mu {)}^T\text{\hspace{1em}(4)}$$
矩阵的转置φ表示为φ^T ,通过计算通过奇异值分解 (SVD) 算法使用的特征向量，在协方差矩阵上执行 PCA 。SVD 定义为复数或实数矩阵 X 的因式分解，使得X= U**S**V，其中 U 和 V 是酉矩阵，即
$$\overline{U^T}\ast U=U\ast \overline{U^T}=I$$
I 是单位矩阵，S 是非负实数对角元素的矩形矩阵。为了将系统从 n 维减少到 k 维，我们从 U 中获取前 K 个向量（列）。

C. 支持向量机 (SVM)

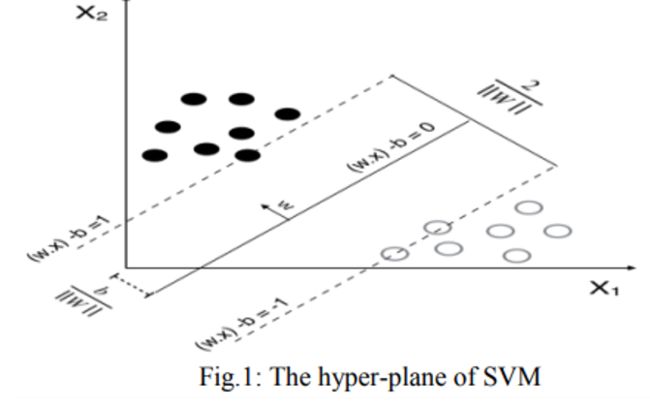
支持向量机的目的是通过找到一个超平面来最大化两个类之间的分离边际。让输入输出数据格式如下
$$(x_1,y_1),...,(x_n,y_n),x\in R^m,y\in \{+1,-1\}$$
(x 1 , y 1 ),……(x n , y n ) 是训练的数据集，其中每个x i是一个m维实向量，n代表样本数，y属于+1或-1，通过指示点 xi属于哪个类。在线性可分的情况下，超平面对数据集进行分类，如图所示

核函数

然而，在大多数情况下，数据不是线性可分的，很难找到超平面来对数据进行分类。所以为了解决这个问题，SVM 有不同的核函数。线性不可分问题可以通过选择合适的核函数来解决。应用内核技巧后得到的算法保持不变，除了线性内核 SVM 中的每个点积都被非线性内核函数替换。
主要的非线性 SVM 核函数是
1.径向基核函数：使用的典型径向基核是高斯核。
$$K(x,y)=exp(-\gamma ||x-y||{)}^2$$
其中 x 和 y 是输入向量。如果γ=σ^− 2那么这个核被称为高斯方差核σ^− 2

2.多项式核函数：计算两个向量之间的 d 次多项式核。两个向量之间的相似性由多项式核表示。
$$K(x,y)=(\gamma (x^{T}y)+c_0{)}^d$$
γ是斜率，d 是核度，C o是截距。如果内核被认为是同质的C 0 = 0.

数据集预处理–转换

KDDCup’99 数据的示例如图 2所示。转换后，系统将数据集中的文本词转换为数值，如图3所示. 例如，如果“Normal”被映射为 0，则攻击类型，系统使用表 3中提供的转换表将文本转换为数值。

数据集预处理 --特征缩放

转换后，数据集被归一化，使每个特征的数值在同一尺度下。在转换和规范化之后，数据集如图 4所示。进行缩放操作是为了降低复杂性，减少重叠并提高准确性。

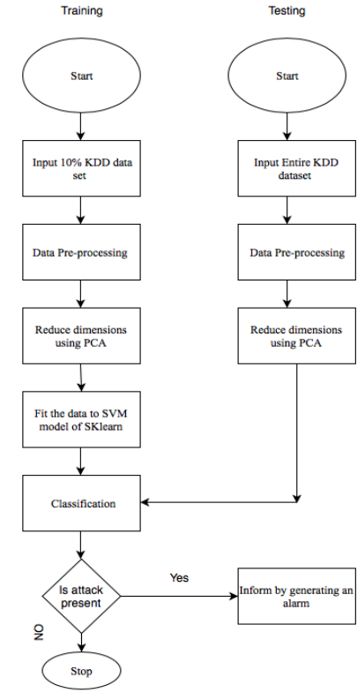
算法过程

两个阶段中，PCA 应用于预处理数据集，以便将高维数据转换为低维数据。通过PCA对训练数据集进行降维后，通过支持向量机算法对预处理后的数据集进行训练，构建训练系统。一旦训练好的系统准备就绪，测试数据集就会被分类，以便在出现攻击时生成警报。通过将 SVM 分类器的预测结果与 KDDCup’99 中的实际结果进行比较来测量准确性，并测量每个测试记录的检测时间。完整的方法在流程图中解释

核函数对比

进行了两个不同的实验，即 with-PCA 和 without-PCA，以评估 PCA 在检测精度上的性能。C 和伽玛( γ) 是 SVM 非线性核中的两个重要参数。C 参数权衡了决策表面的简单性与训练样本的错误分类。较高的 C 通过将更多样本作为支持向量来正确分类所有测试数据集，而较低的 C 使决策表面平滑。另一方面，参数 Gamma 定义了单个训练样本的影响程度，高值表示接近，低值表示远。

总结

从通过实验获得的结果可以看出，当实施 PCA 时，检测率随着尺寸大小的增加而增加，而检测时间减少。在所有实现的内核中，RBF 内核表现出更好的结果和更好的检测率，并且在基于多项式内核的 SVM 中检测速度更快。

不足

论文中没有和不同的监督机器学习算法（例如 K-Nearest Neighbor’s、J48 决策树、随机森林和带 PCA 和不带 PCA 的朴素贝叶斯）来比较和分析 IDS 检测精度和检测时间。

参考论文

[1] Zhang H, Huang L, Wu C Q, et al. An effective convolutional neural network based on SMOTE and Gaussian mixture model for intrusion detection in imbalanced dataset[J]. Computer Networks, 2020, 177: 107315.

[2] P. Nskh, M. N. Varma and R. R. Naik, “Principle component analysis based intrusion detection system using support vector machine,” 2016 IEEE International Conference on Recent Trends in Electronics, Information & Communication Technology (RTEICT), 2016, pp. 1344-1350, doi: 10.1109/RTEICT.2016.7808050.

[3] Almomani, O. A Feature Selection Model for Network Intrusion Detection System Based on PSO, GWO, FFA and GA Algorithms. Symmetry 2020, 12, 1046. https://doi.org/10.3390/sym12061046

[4] A feature selection algorithm for intrusion detection system based on Moth Flame Optimization Arar Al Tawil and Khair Eddin Sabri Conference: 2021 International Conference on Information Technology (ICIT), Year: 2021, Page 377

DOI: 10.1109/ICIT52682.2021.9491690

[5] de Rosa G H, Rodrigues D, Papa J P. Opytimizer: A nature-inspired python optimizer[J]. arXiv preprint arXiv:1912.13002, 2019.