l380废墨收集垫已到使用寿命_涡扇发动机剩余使用寿命周期预测模型
目标综述
这篇文章的主要目的是记录我的一个模型的实现，该模型可用于对商用涡扇发动机进行预测维护。这里使用的预测维护方法是一种数据驱动方法，这意味着从运行中的喷气式发动机收集的数据用于执行预测维护建模。具体来说，该项目的目标是建立一个预测模型，基于类似喷气式发动机集群从运行到故障的数据，以估计剩余使用寿命(RUL)的喷气发动机。本文所述的算法基本遵循[1]。
数据集概述
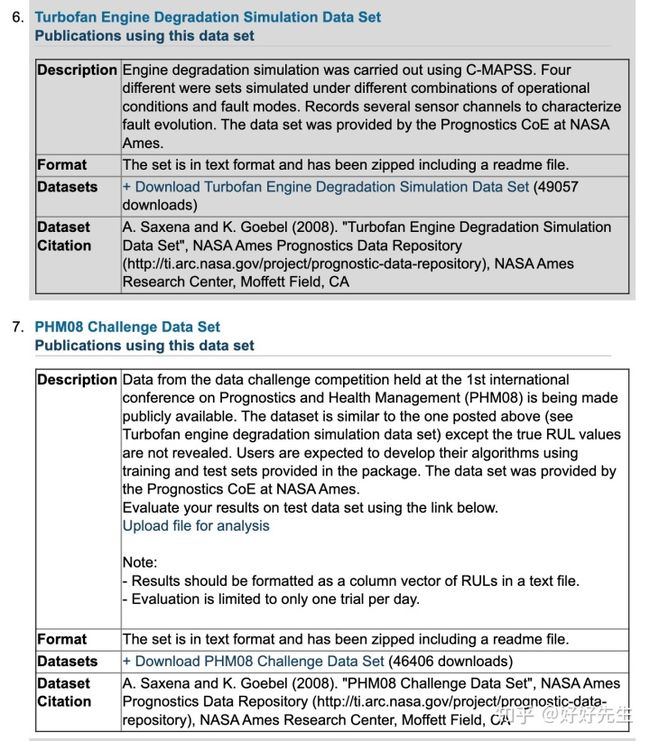
NASA已经创建了预测和健康管理PHM08挑战数据集，并向公众开放。该数据集用于预测喷气发动机随时间的故障。数据集由NASA艾姆斯的预测中心提供数据集包括各种压力、温度和喷气发动机旋转设备速度的时间序列测量。这些测量通常是在商用现代涡轮风扇发动机中进行的。所有的发动机都是同一类型，但每个发动机的启动初始磨损和变化程度不同。这是用户所不知道的。
Prognostics Center - Data Repositoryti.arc.nasa.gov
- 可以使用三个可选设置来更改每台发动机的性能。
- 每个发动机都有21个传感器，在运行时收集与发动机状态相关的不同测量值。
- 模拟了六个不同的飞行条件，其中包括三种运行条件的值范围：高度（0–42K ft。），马赫数（0–0.84）和油门旋转角（TRA）（20–100）。
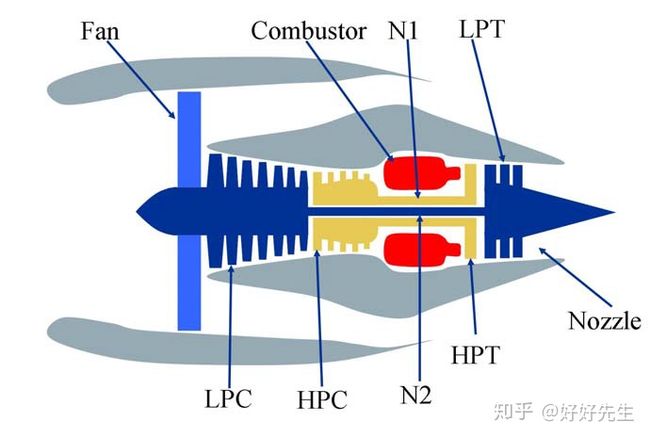
请参阅发动机示意图以及各种传感器测量位置的图片。
采集的数据被传感器噪声污染。随着时间的推移，每台发动机都会出现一个故障，这一点可以通过传感器读数看出来。当特定引擎发生故障时，每个引擎的数据将停止。因此，实际的RUL是根据数据的长度来确定的。数据实际上是使用C-MAPSS(商用模块化航空推进系统仿真)模拟的数据。所生成的模拟数据被用作第一届预测与健康管理(PHM)数据竞赛(PHM 08)的挑战数据。
有关数据集的更多详细信息，请参见飞机发动机从运行到故障模拟的损伤传播建模：
当前的问题是提出一个基于传感器测量的时间序列数据的机器学习模型来预测RUL，这些数据通常来自飞机燃气轮机。
解决方案策略
- 主要策略是使用数据集训练回归模型来预测RUL。 由于数据是许多传感器数据的时间轨迹形式，因此需要将这些传感器数据融合到状态指示器或健康指标中，以帮助识别故障的发生。
- 测试模式下的模型将比较测试融合信号与训练融合信号的相似度/相关度。 基于该相似度比较，进行预测。
由于训练数据由run-to-failure轨迹组成,而测试数据包含未定义的健康状态轨迹,然后训练过程将包括训练的模型部分发生故障前的轨迹模拟真正的使用模型的在线预测模式。
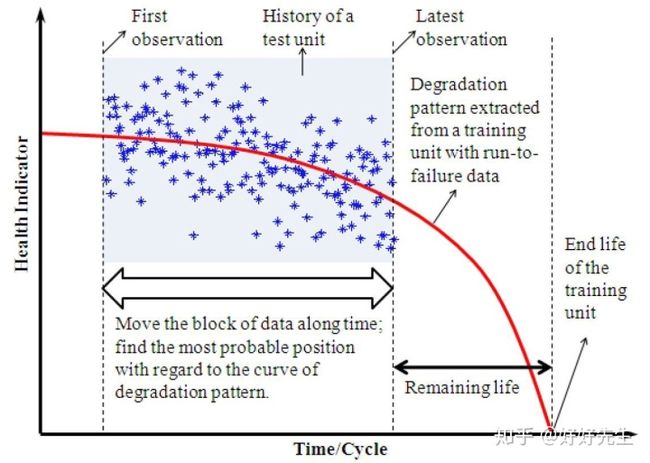
单元是根据具有最相似退化模式的训练单元的实际寿命来估计的。
数据挖掘
本文分析使用的数据是仿真数据的一部分，具体文件为:train FD001.txt。这个特定的数据集包含100个从运行到故障的引擎模拟(对应100个不同的引擎)：
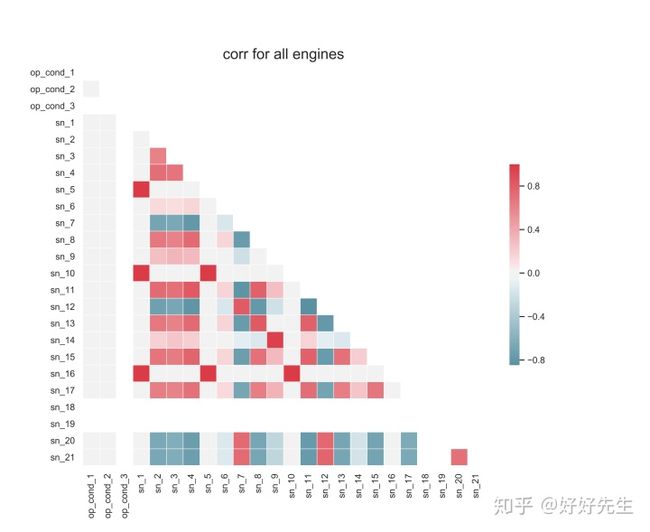
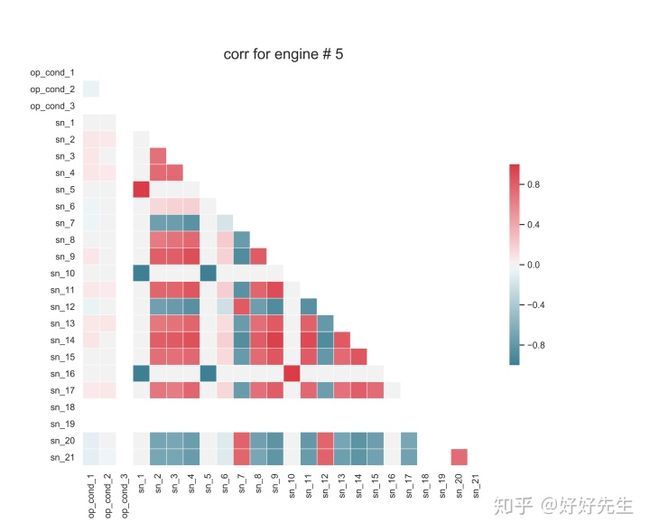
- 从第一眼看，似乎有些传感器彼此之间非常相关。 这似乎适用于所有引擎，也适用于单引擎数据。 这可能会在建模期间引起问题，并且我可能需要删除/融合一些传感器数据。
- 此外，似乎有一些列需要删除，因为它们都是白色的。这可能表示值不变，让我们更深入地研究一下相关性
( 'Sn_1', 'Sn_5', 1.0)
( 'Sn_1', 'Sn_10', 1.0)
( 'Sn_1', 'Sn_16', 1.0)
( 'Sn_5', 'Sn_10', 1.0)
( 'Sn_5', ' Sn_16 ', 1.0)
(' Sn_9 ',' Sn_14 ', 0.9631566003059564)
(Sn_10' ',' Sn_16 ', 1.0)上述传感器之间存在着完美的相关性。这意味着我可以为分析删除一些列。
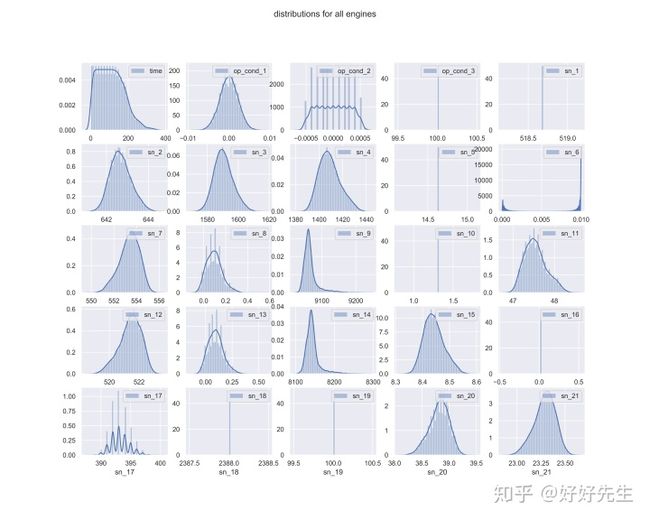
现在让我们看看时间序列图和各种变量的数据列的分布
同样重要的是
- 几乎所有变量的分布都是单斜高斯分布。
- op cond 2和sn 17似乎是离散变量，而不是连续变量(可能需要删除这些变量，以便只保留连续变化的变量进行建模)
- 以上的观察结果适用于绘制所有引擎和特定引擎的绘图。(表示所有引擎的输出响应都非常相似)
columns to be removed from analysis since they do not change with time
['op_cond_3', 'sn_1', 'sn_5', 'sn_6', 'sn_10', 'sn_16', 'sn_18', 'sn_19']high correlation columns all engines:
('sn_9', 'sn_14', 0.9631566003059564)删除不随时间变化的列后，只有传感器9和14的相关度大于0.9
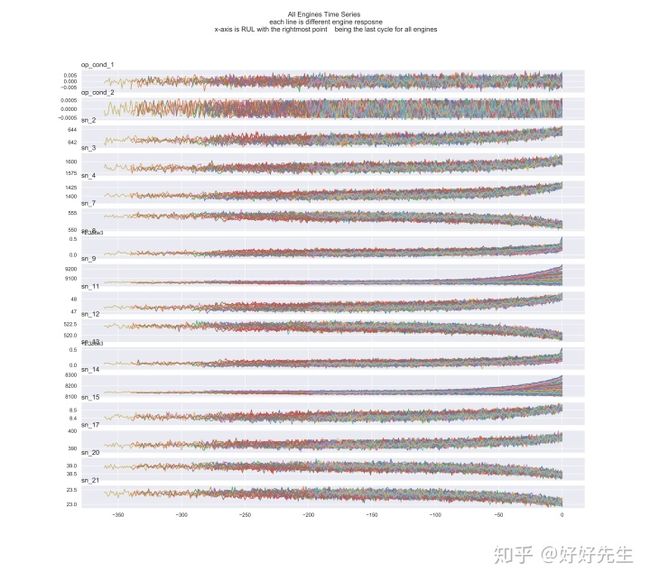
现在，让我们看一下所有发动机的运行周期的原始传感器数据，以了解传感器的时间变化，并瞥见发动机之间的差异：
从所有引擎的时间序列图中，我们可以找到以下要点
- [op_cond_1，op_cond_2]列在引擎使用寿命方面没有明显的趋势。 它们只是随机噪声。 因此，我很有信心地说，这两栏无法帮助基于该系列趋势的预测模型发现有关估计RUL的相关信息
- [s n_9，sn_14]列表示趋势取决于特定引擎。 寿命终止时，有些引擎在这两列中倾向于增加，而另一些倾向于减少。 这两个传感器的共同点是，使用寿命延长了。
- 很高兴看到，当故障在整个发动机循环中传播并导致它们失效时，所有其他列都显示出明显的趋势。 [这将有助于模型尝试使用数据预测RUL :)]
sensors remaining for analysis after considering trends in the time series plot
['sn_2' 'sn_3' 'sn_4' 'sn_7' 'sn_8' 'sn_11' 'sn_12' 'sn_13' 'sn_15'
'sn_17' 'sn_20' 'sn_21']实施方式
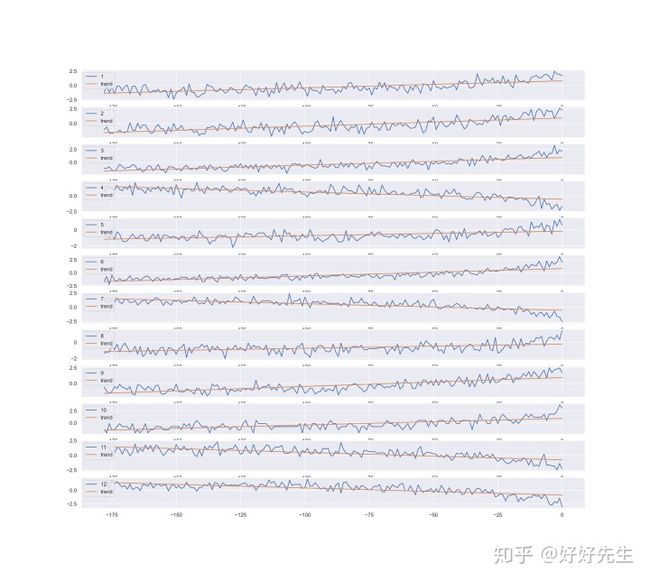
- 线性趋势：
我现在要检查的是剩余传感器作为操作周期函数的趋势。 较高的趋势可能意味着引擎使用寿命结束时事件的可预测性更好。
只需将线性模型拟合到每个传感器即可找到趋势。 然后，我根据传感器的线性斜率绝对值对其进行排序。 当然，在进行线性回归之前，传感器值已被标准化！
the order of trend slope magnitude is
['sn_11' 'sn_4' 'sn_12' 'sn_7' 'sn_15' 'sn_21' 'sn_20' 'sn_17' 'sn_2'
'sn_3' 'sn_13' 'sn_8']2.降维PCA：
我想进一步减少问题的范围。 因此，让我们检查一下PC的前几个Principled Components分别解释了传感器的可变性
第一PC：74％
第二PC：4.1％
第三PC：3.5％
现在使用线性趋势斜率仅包含最高6个传感器的数据子集，让我们再次进行PCA：
第一PC：81.6％
第二PC：5％
第三PC：4.4％
根据线性趋势的分析，根据传感器线性趋势的大小即线性回归斜率的大小来选择前6个传感器。 看起来，基于这6个传感器，采用3个主要原理s可以捕获大约90％的数据可变性。 因此，尺寸的进一步减小带来了信息的低损失。
3. 数据探索和降维总结：
不会随时间变化的传感器（不会随发动机工作周期变化）被丢弃，因为它们没有提供任何信息来预测使用寿命的结束 没有明显趋势的传感器（仅看起来像噪声，或者没有寿命终止趋势的传感器）也会被丢弃。 其中包含的传感器对于不同引擎的行为各不相同（因为它们会混淆学习算法，并可能导致较大的测试错误，因为它们的行为在所有引擎上都不是通用的） 基于剩余传感器数据与RUL的线性回归，就仅保留了斜率绝对值最高的6个传感器。 这些传感器在发动机寿命终止时会发生可预测的变化。 此外，通过采用数据的前3个主成分来降低维数。
数据的其余3个组成部分将融合在一起，以使每个引擎具有RUL的运行状况指数（HI）功能.
融合传感器：
要创建融合健康指数（HI）传感器，首先，我们需要训练极端数据（发动机循环开始时和发动机循环寿命结束时的数据）。
生命开始时值为1，生命结束时值为0。
因此模型将获取传感器值并找到给出健康指示HI的融合信号。
我将具有良好运行状况的引擎称为具有（RUL_hgih = 300）个或更多周期直到故障的引擎。 零健康状况被视为每个发动机操作的最后（RUL_low = 5）个周期。
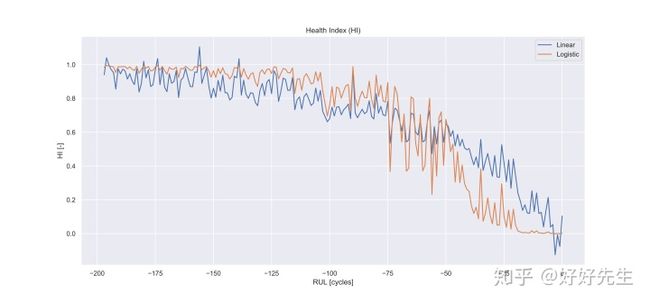
- 上图显示了将所有传感器融合为一个信号（健康指数（HI））的结果。 上面的结果是针对代表性引擎的。 请注意，HI可以通过各种融合技术获得，这里我仅展示了使用线性和逻辑回归模型的融合。
- 请注意逻辑回归如何严格在[0,1]之间给出值，而线性回归模型不能保证这一点。
- 在接下来的分析中，决定使用线性模型融合信号
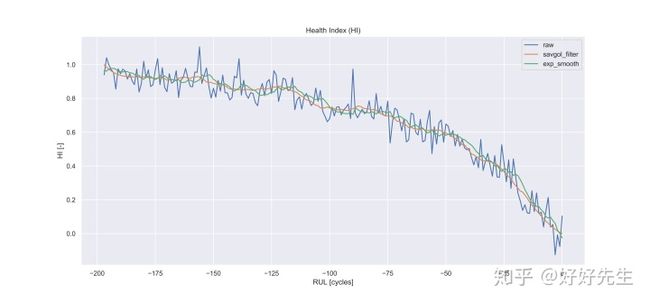
- 由于HI噪声较大，因此将应用一次平滑处理。在剩余的分析中使用Savitzky-Golay（Sav_gol）滤波器
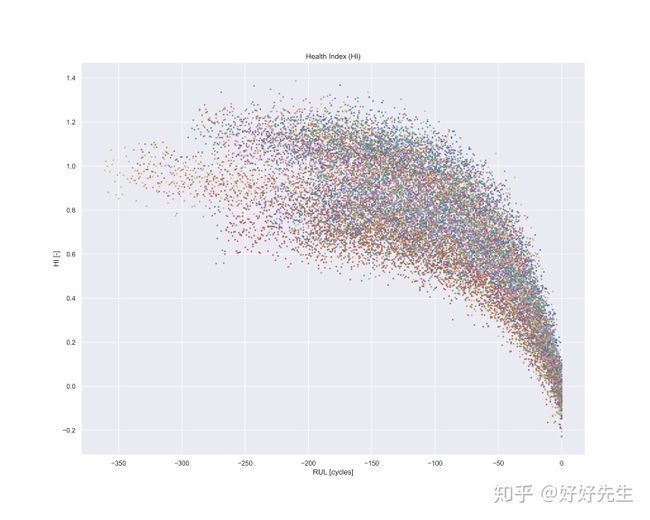
值得一提的是，它们各自的HI都有发动机之间的差异。 当然，这是可以预料的，因为发动机的原始未融合传感器具有可变性。 见下图：
拟合模型
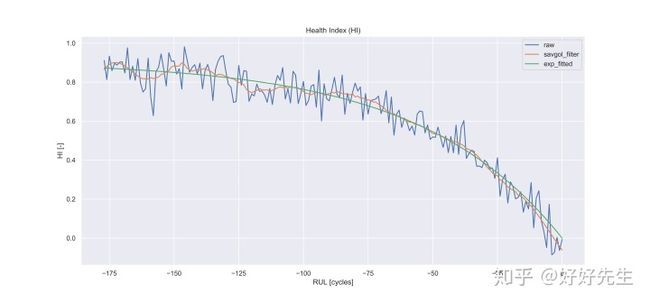
我们将在模型中使用HI的方法是为每个引擎创建一个简单的指数模型：
y = a [exp（b * t）-1] = HI，
然后使用该HI指数拟合R之间的相似性来预测RUL 为新发动机安装的HI和原始HI。 下图显示了代表性发动机的指数拟合HI曲线以及原始HI和过滤后的HI
上面的培训模型摘要：
该算法的训练模型只是从其时间序列传感器中找到给定引擎的健康指数（HI）。训练结果是一个指数模型，该模型给出了发动机的HI作为其先前工作循环（其剩余寿命RUL）的函数，其步骤可总结如下：
- 在移除所有发动机中寿命低或变化不明显的传感器后，我们将得出传感器数据 =（ 1， 2，…， ），其中 是传感器（列）的数量数据清理后的剩余传感器数据的集合
- 使用StandardScalar标准化to以获得X__
- 用RUL（发动机工作循环）求出每个 xi的线性趋势（斜率）
- 从 _ 中，选取 个传感器的子集，这些子集具有 最高的绝对线性斜率，新的子集为
- 在 上执行PCA，以缩小到 列的空间。最后一个传感器子集称为
- 使用 ，线性模型用于将 n个传感器融合在一起以产生一维传感器
线性模型是通过从取一个子集获得的，该子集对应于大于 ℎ ℎ且小于 的运算周期。 周期大于 ℎ ℎ的传感器值被映射为1（因为它们具有接近完美的运行状况），而周期小于 的传感器值则被映射为0，因为它们几乎没有剩余寿命。 请注意，该子集取自所有引擎，因此此融合模型是整个引擎集的全局模型。
= ^ _ + 0，其中 是上述线性回归模型的结果。
现在，可以应用线性模型将每个发动机循环中所有发动机的传感器值融合并转换为 。
最后，对于 对于每个发动机获得的值被模制为一个指数曲线，它为健康指数 一个模型作为发动机循环的函数的所有引擎在所述数据集.
预测新引擎RUL —提前过程
接下来是基于运行周期小于整个生命周期的传感器值来预测新发动机的RUL的算法。
我将主要使用插值方案将新引擎与从培训中获得的健康指数模型库进行比较。
预测新引擎RUL
输入：
新引擎RUL的预测作为输入：
1.具有观察力的融合传感器等于新发动机的当前寿命周期
2.为所有训练有素的引擎拟合HI的指数模型
查找/比较相似性
然后，该模型会尝试从训练阶段开始，将新发动机的融合传感器的观测结果与模型库中的HI模型（指数拟合曲线）进行比较。
- 基本上，模型找到融合传感器与库中每个拟合模型之间的平方差之和（SSD），并将此SSD定义为融合传感器与库中每个发动机模型之间的相似性度量。
- 由于通常新引擎融合传感器的总观测值（M）小于模型库引擎观测值（Ti），因此模型也会随时间移动融合传感器曲线（按周期间隙参数），从而为每个引擎找到多个SSD模型。每个训练引擎的SSD数量取决于融合传感器与训练引擎观测值之间的差异（Ti — M）
- 获得来自每个训练引擎的最小SSD以及针对新引擎的相应的估计的RUL。
- 该模型现在具有N个估计的RUL和关联的N个SSD，需要融合以给出测试引擎的最终RUL。 N是训练集中的引擎总数
RUL融合和最终模型输出
N个估计的RUL被减小为N_red RUL。 通过消除从具有高SSD（低相似性）的发动机模型预测的RUL以及通过考虑与训练集的统计相关的信息（简单的异常值消除）来实现减少
然后将N_red RUL融合为一个RUL，这是模型的最终输出。
做到这一点的方法是使用N_red RUL的加权平均值或采用RUL的中值（方法1）。 这里使用了三种不同的权重：
- 基于SSD的加权平均值，对于低SSD的加权平均值更高（方法2）
- 最小最大加权，其中只有较低的RUL使用较高的权重对N_red中的最大和最小RUL进行加权，因为它比较保守，因此比较可取（方法3）
- 简单的算术平均值，其中所有权重均等于方法4）
模型评估和验证：
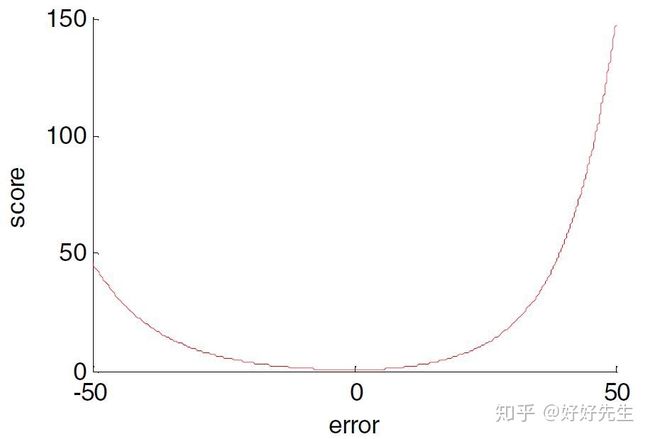
对于RUL估计，早期预测优于晚期预测。 因此，模型的计分在真实的故障时间周围是不对称的，因此较之早的预测，后期的预测将受到更大的惩罚。 无论哪种情况，惩罚都会随着误差的增加而呈指数增长。 非对称偏好由下面给出的评分函数中的参数a1和a2控制
必须指出的是，预测更远的未来要比寿命接近尽头的预测困难。 这意味着，在实际发动机健康状态非常高的情况下（预计在故障发展为重大故障之前，发动机需要很长时间），预计模型的准确性会更差。
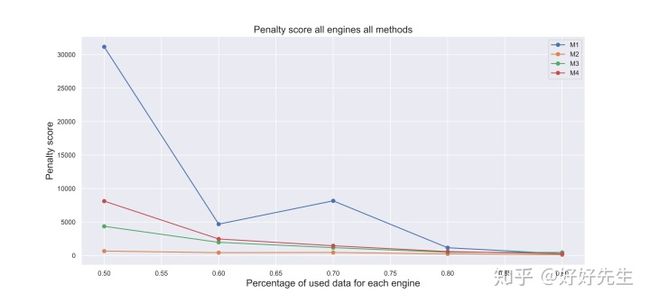
从上面的数据显示点球得分(点球得分较低的值更好的准确性)和观测的总百分比数据四个不同的方法,我们可以作出以下评论最终模型性能新引擎数据:
- 方法2(基于SSD加权平均融合原则)是最好的点球得分。即使从使用数据的低百分比(即预测更多的未来)来看，该方法也表现得异常出色。
- 所有的方法似乎都非常相似，当使用的数据的百分比高，即当测试引擎当前运行周期接近总寿命的引擎。这是可以预料到的，因为预测未来的几个周期比较容易，预测未来的大周期也比较容易。
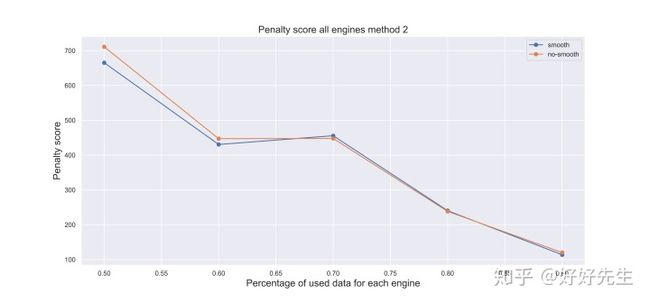
- 在将测试数据输入模型之前对其进行平滑处理似乎效果甚微。然而，对于所有的方法和百分比，平滑数据会得到更好的分数。
端到端问题解决方案总结：
问题：
考虑到类似喷气发动机样本上各种传感器的故障测量结果，估计在相同时间段内测量同一传感器的新喷气发动机的剩余使用寿命（RUL）。
解：
- 对于每次运行至失败的测量，请选择对使用寿命周期具有可预测的高趋势的传感器
- 使用这些传感器，制作一个模型，将这些传感器融合在一起，以给出虚拟的一维健康指数（HI），该指数从周期开始时的大约1变化到接近寿命的0。
- 为故障引擎的每次可用运行建模并存储这些HI，并将HI称为“模型”
- 使用新的发动机测量值，将其测量值融合以生成融合的HI。
- 将此HI与模型库中存在的HI模型进行比较
- 在模型引擎的RUL的基础上找到新引擎的RUL。
改善：
- 代码结构改进
- 创建一个采用输入传感器并提供融合HI传感器作为输出的转换管道
- 创建/固有的sklearn估计器，并将此处的拟合和预测方法合并为一个估计器，以易于使用并针对以下情况使用适当的交叉验证
- 根据数据内部条件，自动选择传感器
算法改进
- 使用与线性回归模型不同的模型来融合传感器
- 使用即将训练或基于输入传感器测量直接训练以预测RUL的神经网络模型，而不是准备一维健康指标。 此选项似乎很有希望，并且应该提供更好的准确性，但是需要更多的计算资源，但是消除了特征工程过程，并且可以更好地推广
- 使用交叉验证选择各种模型参数，而不使用启发式方法。 这些改进需要首先创建自定义估算器和自定义转换器
References:
[1] T. Wang, J. Yu, D. Siegel, J. Lee, “A similarity-based prognostics approach for remaining useful life estimation of engineered systems”, Proc. Int. Conf. Prognostics Health Manage., pp. 1–6, Oct. 2008
[2] Chao Hu, Byeng D. Youn, Pingfeng Wang, Joung Taek Yoon,
“Ensemble of data-driven prognostic algorithms for robust prediction of remaining useful life”, Reliability Engineering & System Safety, Volume 103, 2012, Pages 120–135, ISSN 0951–8320, https://doi.org/10.1016/j.ress.2012.03.008.
